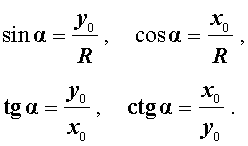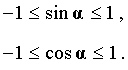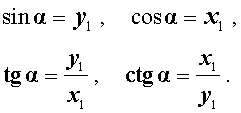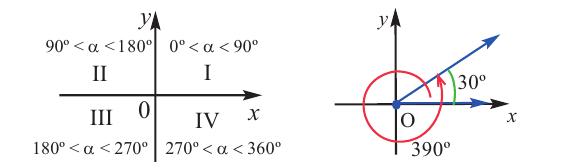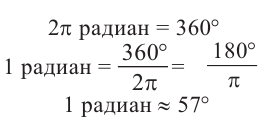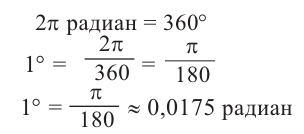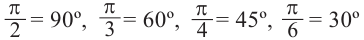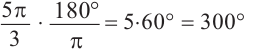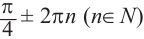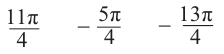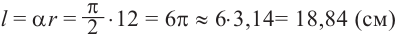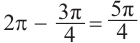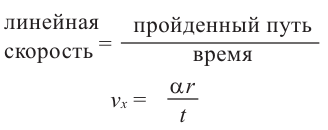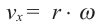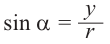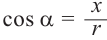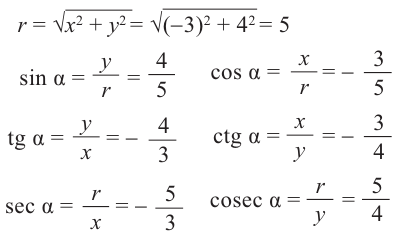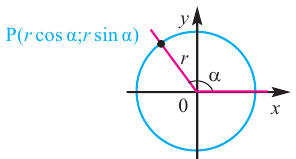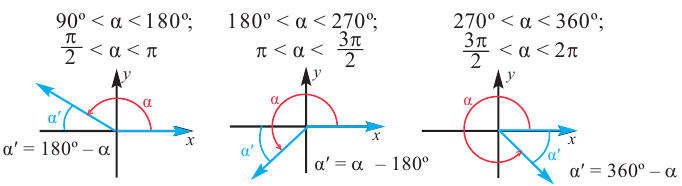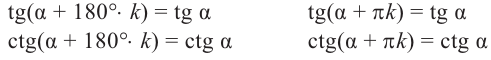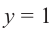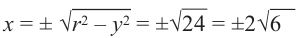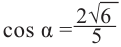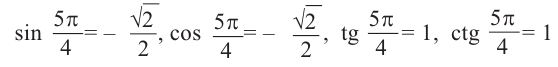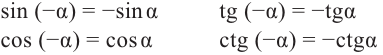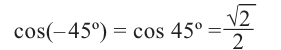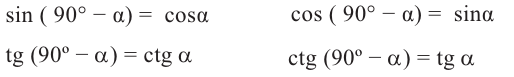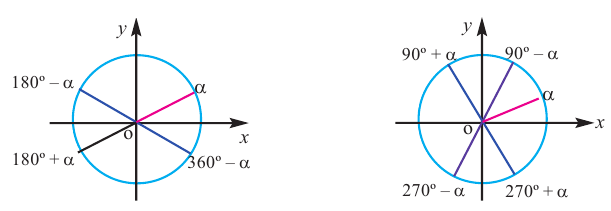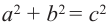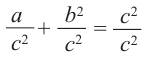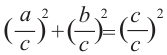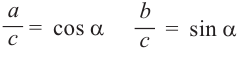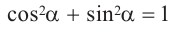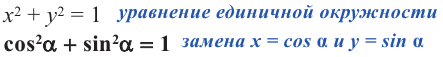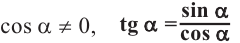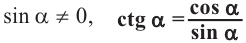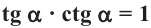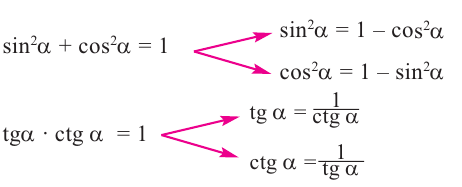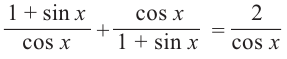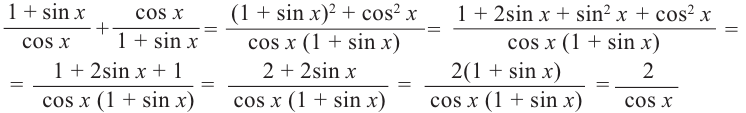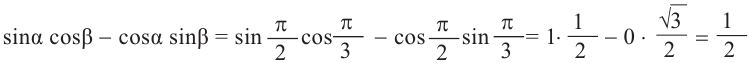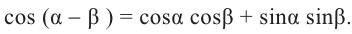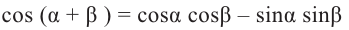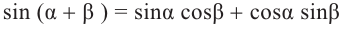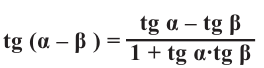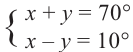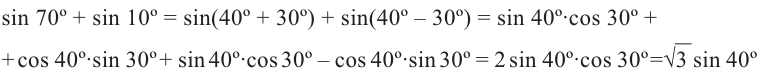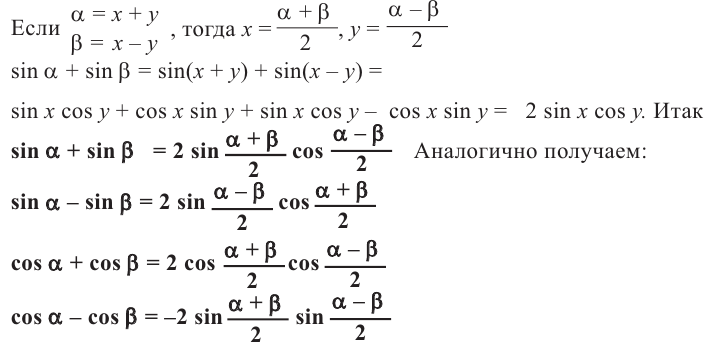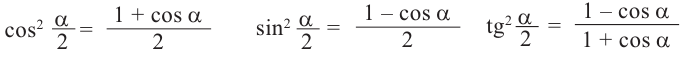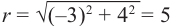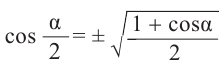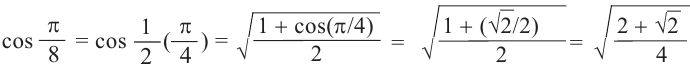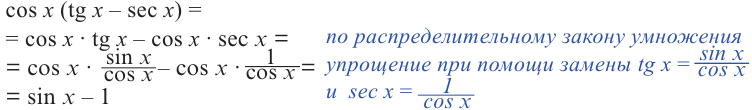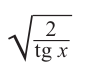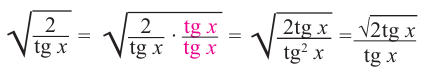Видеоурок: Синус, косинус, тангенс и котангенс угла
Лекция: Синус, косинус, тангенс, котангенс произвольного угла

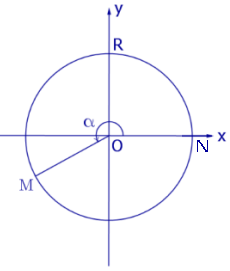
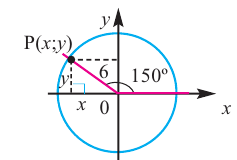
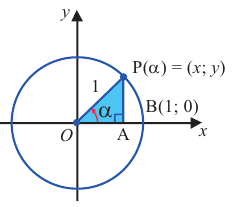
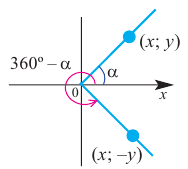
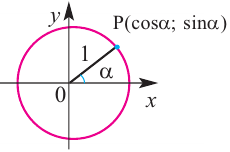
Чтобы понять, что такое тригонометрические функции, обратимся к окружности с единичным радиусом. Данная окружность имеет центр в начале координат на координатной плоскости. Для определения заданных функций будем использовать радиус-вектор ОР, который начинается в центре окружности, а точка Р является точкой окружности. Данный радиус-вектор образует угол альфа с осью ОХ. Так как окружность имеет радиус, равный единице, то ОР = R = 1.
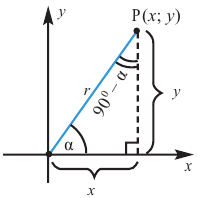
Если с точки Р опустить перпендикуляр на ось ОХ, то получим прямоугольный треугольник с гипотенузой, равной единице.
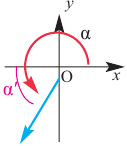
Если радиус-вектор двигается по часовой стрелке, то данное направление называется отрицательным, если же он двигается против движения часовой стрелки — положительным.

Синусом угла данной окружности, образованного радиусом-вектором ОР, является ордината точки Р вектора на окружности.
То есть, для получения значения синуса данного угла альфа необходимо определиться с координатой У на плоскости.
Как данное значение было получено? Так как мы знаем, что синус произвольного угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе, получим, что
А так как R = 1, то sin(α) = y0.
В единичной окружности значение ординаты не может быть меньше -1 и больше 1, значит,
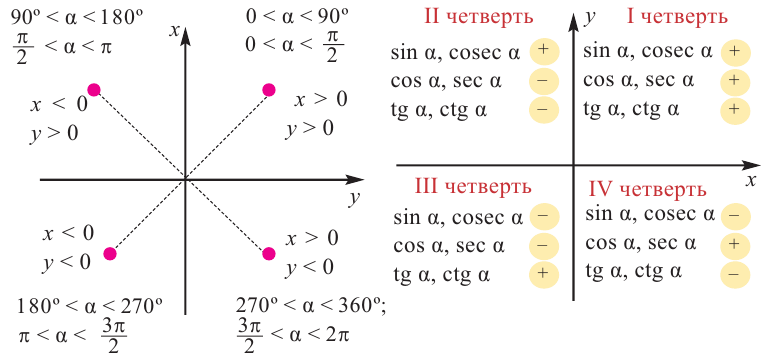
Синус принимает положительное значение в первой и второй четверти единичной окружности, а в третьей и четвертой — отрицательное.
Косинусом угла данной окружности, образованного радиусом-вектором ОР, является абсцисса точки Р вектора на окружности.
То есть, для получения значения косинуса данного угла альфа необходимо определиться с координатой Х на плоскости.
Косинус произвольного угла в прямоугольном треугольнике — это отношение прилежащего катета к гипотенузе, получим, что
А так как R = 1, то cos(α) = x0.
В единичной окружности значение абсциссы не может быть меньше -1 и больше 1, значит,
Косинус принимает положительное значение в первой и четвертой четверти единичной окружности, а во второй и в третьей — отрицательное.
Тангенсом произвольного угла считается отношение синуса к косинусу.
Если рассматривать прямоугольный треугольник, то это отношение противолежащего катета к прилежащему. Если же речь идет о единичной окружности, то это отношение ординаты к абсциссе.
Судя по данным отношениям, можно понять, что тангенс не может существовать, если значение абсциссы равно нулю, то есть при угле в 90 градусов. Все остальные значения тангенс принимать может.
Тангенс имеет положительное значение в первой и третьей четверти единичной окружности, а во второй и четвертой является отрицательным.
Котангенсом произвольного угла называется отношение косинуса к синусу.
Рассматривая прямоугольный треугольник — отношение прилежащего катета к противолежащему, то есть абсциссы к ординате.
Так как ордината находится в знаменателе дроби, то котангенс не может существовать при угле альфа, равном нулю градусов.
Котангенс принимает те же значения в четвертях единичной окружности, что и тангенс.
Все перечисленные функции являются периодичными. Косинус и синус имеют период 360 градусов, то есть 2Пи, а тангенс и котангенс 180 градусов, то есть Пи.
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
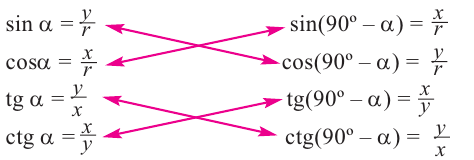
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и
Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .
Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
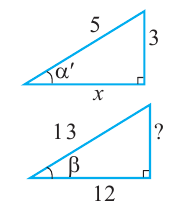
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:
Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:
AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.
Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.
Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.
Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB — BH = 18 — 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.
Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.
Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.
Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.
Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:
Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:
Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:
Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:
В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:
A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:
Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:
1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:
Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:
Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:
Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 — = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.
Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Тригонометрические функции произвольного угла
Содержание
Определение тригонометрических функций произвольного угла
Рассмотрим окружность радиуса R с центром в начале прямоугольной системой координат Oxy.
Рис.1
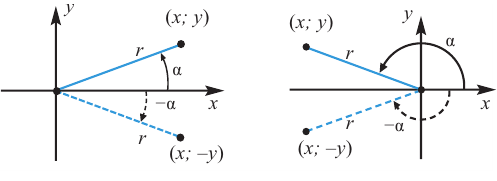
Положительным считается угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении движения против часовой стрелки (рис.1).
Рис.2
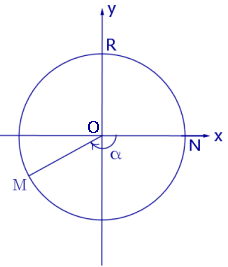
Отрицательным считается угол NOM, сторона OM которого получена из положительной полуоси Ox в результате поворота, осуществляемого в направлении, совпадающем с направлением движения часовой стрелки (рис. 2).
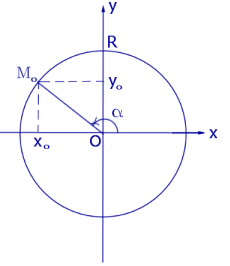
Если для координат точки M0 , лежащей на окружности радиуса R с центром в начале координат O (рис. 3),
Рис.3
ввести обозначение
M0 = ( x0 ; y0 ),
то, в силу теоремы Пифагора, будет справедливо равенство:
x02 + y02 = R2,
и можно сформулировать следующее общее определение тригонометрических функций произвольного угла.
Синусом, косинусом, тангенсом и котангенсом произвольного угла α называют числа, определяемые по формулам:
ЗАМЕЧАНИЕ 1. Отметим следующее важное свойство тригонометрических функций синуса и косинуса произвольного угла:
ЗАМЕЧАНИЕ 2. Определение тригонометрических функций произвольного угла является естественным обобщением определения тригонометрических функций острого угла, данного в разделе справочника «Тригонометрические функции острого угла».
Основное тригонометрическое тождество. Тригонометрический круг
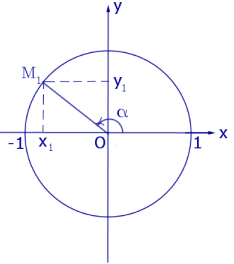
Рассмотрим окружность радиуса 1 с центром в начале координат. Если для координат точки M1 (рис. 4), лежащей на этой окружности,
Рис.4
ввести обозначение
M1 = ( x1 ; y1 ) ,
то, в силу теоремы Пифагора, будет справедливо равенство
x12 + y12 = 1 ,
а синус, косинус, тангенс и котангенс угла α будут вычисляться по формулам
Из этих формул, в частности, вытекает основное тригонометрическое тождество:
sin2α + cos2α = 1 .
Таким образом, основное тригонометрическое тождество является теоремой Пифагора, сформулированной с помощью тригонометрических функций.
Окружность радиуса 1, изображенную на рисунке 4, называют тригонометрическим кругом или числовой окружностью.
Содержание:
Тригонометрические функции произвольного угла
Угол поворота
До недавнего времени говоря об угле мы имели в виду угол, полученный между двумя неподвижными сторонами. Угол также можно рассматривать как измерение поворота. Например, радиус колеса, расположенного по горизонтали при вращении вокруг неподвижной оси, через определённое время относительно начального положения образует некоторый угол. К тому же значение угла зависит от направления поворота. Любой угол можно рассматривать как фигуру, полученную вращением луча вокруг начальной точки.
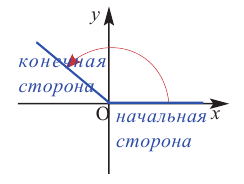
Начальное положение луча соответствует одной стороне угла, конечное положение — другой стороне. При вращении луча на координатной плоскости относительно начала координат в направлении по часовой стрелке или против часовой стрелки, можно получить различные углы.
Начальная сторона угла поворота совпадает с положительным направлением оси абсцисс. Сторону, полученную при вращении относительно начала координат (вершины угла), назовём конечной стороной. Принято считать, что если поворот происходит в направлении против часовой стрелки, то угол имеет положительное значение, при повороте в направлении по часовой стрелке, угол имеет отрицательное значение,
положительный угол отрицательный угол
Координатные оси разбивают координатную плоскость на 4 четверти. Значение угла, в зависимости от того, в какой четверти расположена его конечная сторона, меняется в определенном интервале.
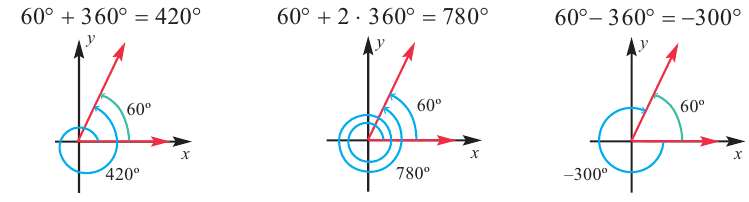
Конечная сторона угла может совершить один или несколько оборотов относительно начала координат. Один полный оборот соответствует углу 360°. Существует бесконечное число углов поворота, у которых начальная и конечная стороны совпадают. Например, конечные стороны углов 30°и 390° совпадают. В общем, для углов поворота 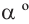
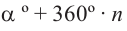
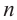
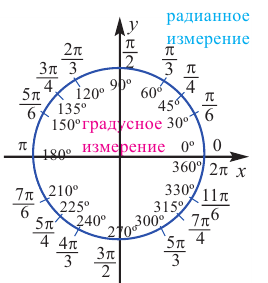
Радианная и градусная мера угла
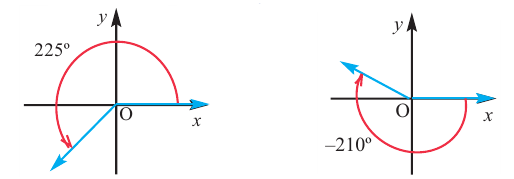
Пример 1. Нарисуйте угол заданной величины. Определите какой четверти принадлежит конечная сторона угла.
Пример 2. На координатной плоскости покажите и запишите градусные меры двух положительных и одного отрицательного угла поворота, конечные стороны которых совпадают с конечной стороной угла 60°.
Радианное измерение углов
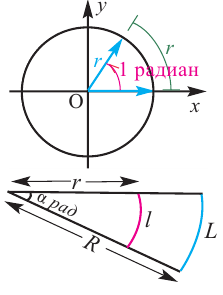
Угол в один радиан-это центральный угол, у которого длина дуги равна радиусу. Радианная мера угла есть отношение длины соответствующей дуги к радиусу окружности: 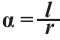
Пример 1. Сколько радиан составляет центральный угол, длина дуги которого равна 12 см, если радиус окружности равен 4 см?
Решение: 1 радиан соответствует длине дуги 4 см. Дуге длиной 12 см будет соответствовать угол 12 : 4 = 3 радиан. Длина окружности 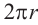
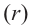
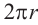
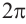
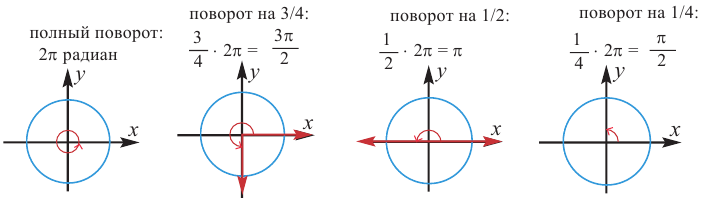
Радианная мера одного целого оборота равна 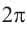
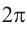
Преобразование градусов в радианы:
Таким образом, 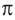
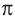
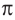
Используя соответствующие радианные и градусные меры углов, расположенных в первой четверти, можно найти увеличенные в разы значения других углов. Например, если 30° =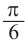
Пример 2. Выразите углы, заданные в градусах радианами, а углы, заданные радианами в градусах, а) 60° ; б)
Решение.
а)60° =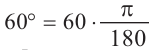
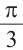

б)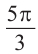
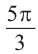
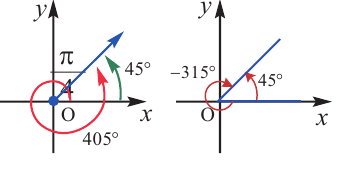
Пример 3. Выразите углы, конечная сторона которых совпадает с углом 45°, в градусах и радианах.
Решение: Конечная сторона угла 45°совпадает с углами 405° и 315°, а также существует бесконечно много углов, конечные стороны которых совпадают с конечной стороной угла 45°: 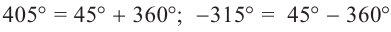
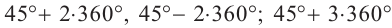
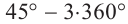
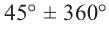
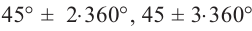
В радианах это можно записать как
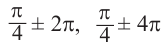
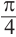
Пример, а)
Все углы поворота, конечные стороны которых совпадают с углом
можно найти но формуле 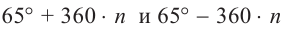
Как видно, в заданном интервале, расположен всего один угол 425°. Пример. д)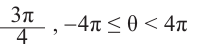
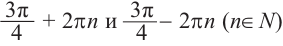
Интервалу 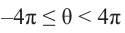
Длина дуги
Запишем формулу нахождения длины дуги, соответствующей центральному углу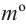
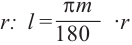
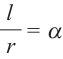
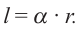
Площадь сектора
Центральному углу 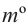
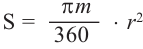
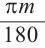
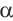
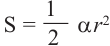
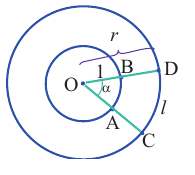
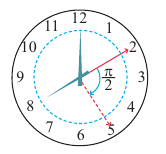
Решение. Секундная стрелка за 60 минут совершают один полный оборот. Это соответствует 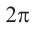
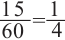
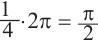
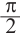
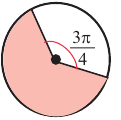
Пример 2. Найдите площадь и периметр закрашенного сектора на рисунке, если радиус круга равен 8 см. Закрашенной части круга соответствует центральный угол:
Площадь сектора равна:
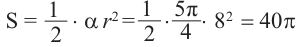
Периметр сектора равен сумме длин двух радиусов и длины дуги: 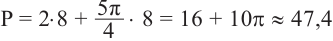
Линейная скорость и угловая скорость
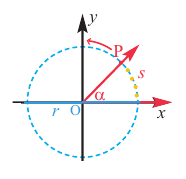
Скорость при движении по окружности, например, скорость движения произвольной точки Р колеса, которое вращается вокруг точки О, может быть вычислена двумя способами.
В первом случае, её можно найти используя расстояние и время. Эта скорость называется линейной скоростью. Во втором случае — используя угол поворота (центральный угол). Эта скорость называется угловой скоростью.
Если тело движется но окружности, то линейная скорость равна отношению пройденного пути (длины дуги окружности) к промежутку времени.
Если тело движется по окружности, то угловая скорость равна отношению угла поворота к промежутку времени.
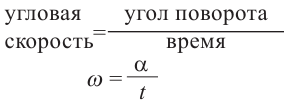
линейная скорость = 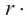
Пример 3. Карусель совершает за минуту 8 полных оборотов.
а)Чему равна угловая скорость карусели за минуту(в радианах)?
б)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 3 м от центра окружности?
в)На сколько метров за минуту передвигается лошадь, которая находится на расстоянии 2 м от центра окружности?
Решение:
а) Один целый оборот при вращении соответствует центральному углу 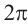
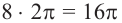
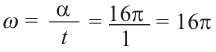
б)Если лошадь находится на расстоянии 3 м от центра, то она движется по окружности радиуса 3 м.
Линейная скорость: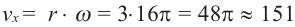
в)Если лошадь находится на расстоянии 2 м от центра, то она движется по окружности радиуса 2 м.
Линейная скорость: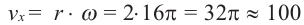
Тригонометрические функции
Тригонометрические отношении для угла зависят только от значения угла.
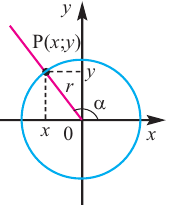
Пусть конечная сторона угла а при повороте пересекается с окружностью радиусом г, центр которой находится в начале координат, в точке Р(х; у).

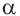

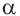

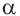
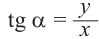
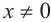

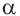
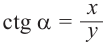
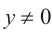

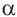
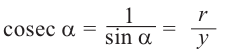
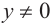

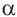
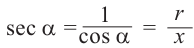
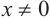
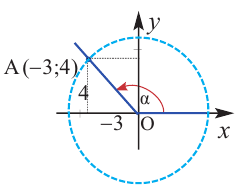
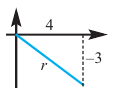
Пример 1. Точка А (- 3; 4) расположена на конечной стороне угла поворота 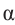
а) Изобразите решение примера.
б) Определите значения тригонометрических отношений для угла поворота 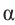
Решение:
а)
б)
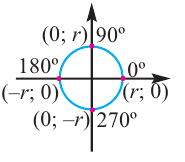
Координаты точки на окружности
Если заданная точка Р окружности находится на конечной стороне угла поворота 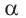
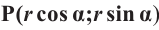
Пример 2. По данным рисунка найдите координаты точки Р.
Точка Р находится во II четверти и косинус отрицательный.
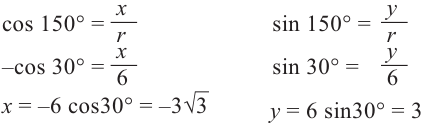
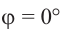
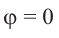
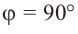
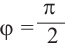
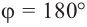
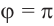
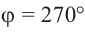
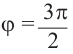
В этом случае координаты х или у равны или нулю, или абсолютному значению длины радиуса.
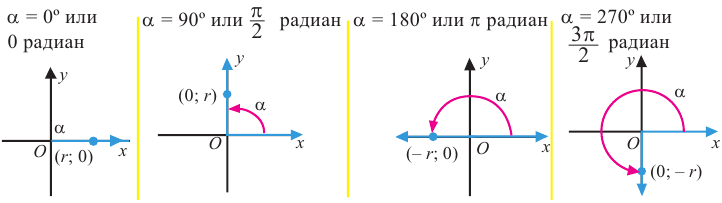
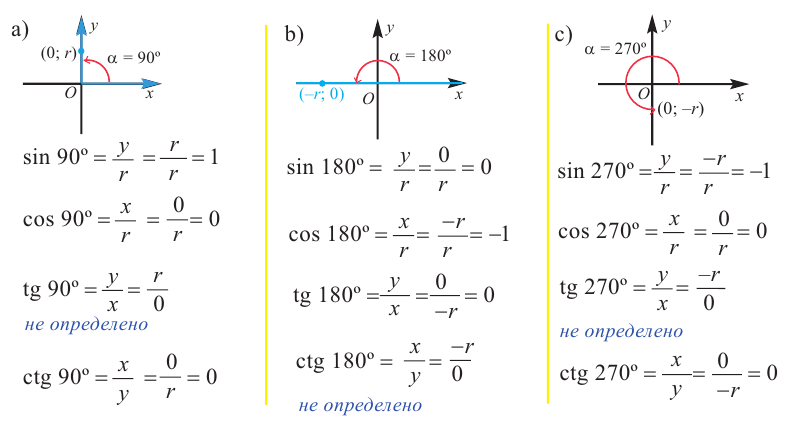
Пример 3. Найдём значения тригонометрических отношений для:
а) а = 90° ; б) а = 180°; в) а = 270° .
При всех допустимых значениях, каждому значению 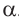
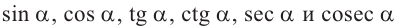
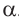
Так как 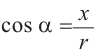
Так как 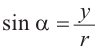
Тригонометрические функции произвольного угла. Нахождение значений тригонометрических функций произвольного угла при помощи острого угла
Чтобы вычислить тригонометрические отношения для углов больше 90°, удобно использовать тригонометрические отношения острого угла.
Для любого угла поворота 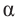
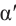
Используя соответствующие острые углы можно определить тригонометрические отношения для любого произвольного угла. Эти значения можно вычислить точно для углов 30°, 45°, 60°, а для остальных острых углов — при помощи калькулятора.
Пример 1. Для следующих углов, определите острые углы:
а)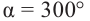
Решение:
а) конечная сторона угла 300° расположена в IV четверти. Соответствующий острый угол равен: 360°- 300° = 60°
б) конечная сторона угла расположена в III четверти. Соответствующий
Пример 2. Найдём значение основных тригонометрических функций для угла 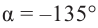
1.Найдём наименьший положительный угол, конечная сторона которого совпадает с заданным углом и дополняет его до 360°: -135° + 360° = 225°
2.Для угла 225° найдём соответствующий острый угол 225° — 180° = 45°.
3.Определим какой четверти принадлежит угол -135° — угол III четверти.
4.Найдём значение тригонометрических функций для угла 45° и учтём знак этих функций в III четверти. Получим:
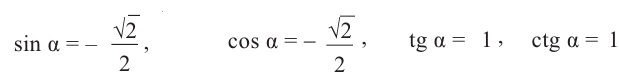
•определяем соответствующий острый угол;
•находим значение тригонометрических функций для этого угла;
•определяем знак значения тригонометрических функций в зависимости от четверти.
Так как конечные стороны углов 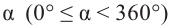
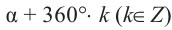
Заметим, что если угол меняется на пол оборота, то значения тангенса и котангенса не изменяются.
На самом деле, если углу поворота 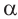
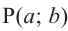
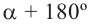

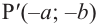
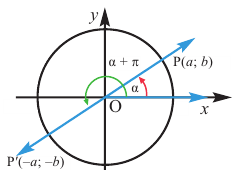
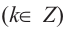
Пример 3. Найдём допустимые значения 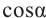
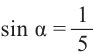
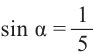
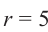
Абсцисса этой точки
Тогда 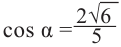
Единичная окружность и тригонометрические функции
Значения тригонометрических функций зависят только от значения угла 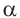
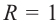
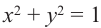
Если точка 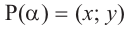
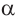
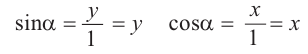
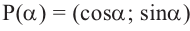
Также по заданным координатам можно найти следующие тригонометрические функции: 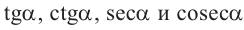
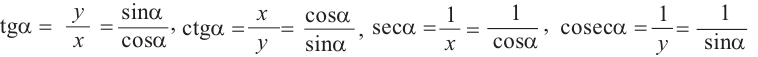
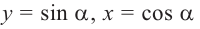
Для этого надо выполнить следующие шаги:
1) На единичной окружности отметим точки, соотвегствующие углу поворота 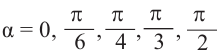
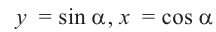
2)Для некоторой точки, принадлежащей единичной окружности, например 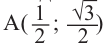
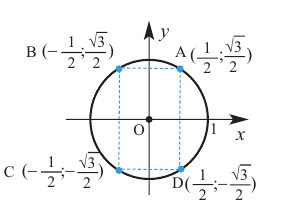
Точка В симметрична точке А относительно оси у, точка С — относительно начала координат, а точка D — относительно оси х. Абсолютные значения координат этих точек равны и отличаются только знаком.
3)Таким образом, можно определить координаты новых точек, зная координаты точки, принадлежащей I четверти. Т.е. получаем единичную окружность, на которой отмечены углы поворота и координаты точек.
- Заказать решение задач по высшей математике
Единичная окружность и тригонометрические функции произвольного угла
Так как координаты точек на единичной окружности удовлетворяют условиям 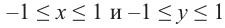
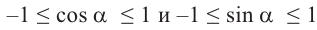
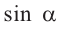
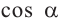
Пример 1. Для угла поворота 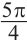
Решение: Конечная сторона угла поворота 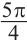
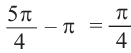
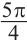
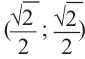
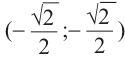
Тогда ,
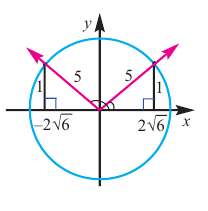
Пример 2. Точка А, с абсциссой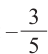
а)Найдём ординату точки А.
б)Изобразим рисунок, соответствующий условию и для угла 
Решение:
а)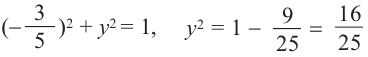
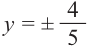
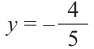
б)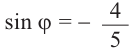
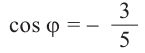
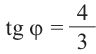
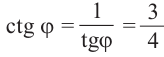
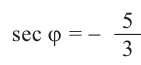
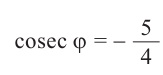
Пример 3. Найдём наибольшее и наименьшее значение выражения 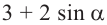
Решение:
Таким образом, для выражения 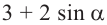
Формулы приведения
Если объект находится в I четверти, то симметричный ему относительно оси у объект находится во II четверти. Симметричный последнему относительно оси х, объект находится в III четверти, и он совпадает с объектом, симметричным начальному объекту из I относительно начала координат. Обратите внимание, что отображение относительно оси у и отображение, относительно оси х, совпадают с поворотом на 180°.
При отображении относительно оси х, точка расположенная на конечной стороне угла изменяет координаты, как показано на рисунке.
То есть, при этом знак меняет только координата у. Таким образом, так как косинус зависит от х он не меняется, зато меняется знак синуса. Отсюда, для углов 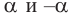
То есть, синус, тангенс и котангенс нечётные функции, косинус-чётная.
Пример 1:
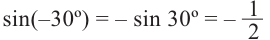
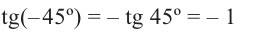
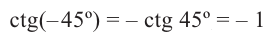

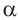
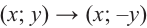
Отсюда получаем:
Запишем для углов 


При попарном сравнении равенств можно увидеть следующую связь-между значениями тригонометрических функций углов 

Повернём конечную сторону угла поворота 
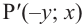
Запишем эти формулы в следующем виде:
Как видно но рисунку отображения относительно оси у и оси х эквивалентны повороту на 180°. Изменение координат, можно записать следующим образом:
Как видно по рисунку, при повороте угла а на 180° конечная сторона расположена в противоположных четвертях, но на одной прямой.
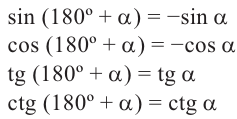
Пример 2.
Для получения аналогичных формул тригонометрических функций угла поворота 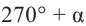
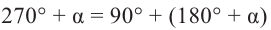
Например:
Теперь запишем соответствующие формулы для угла поворота 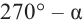
При помощи полученных формул можно найти значения тригонометрических функций произвольного угла, зная значения для соответствующего острого угла. Эти формулы называются формулами приведения. Для формул приведений можно легко увидеть следующую закономерность
1)Если аргумент имеет вид 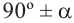
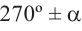
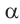
2)Если аргумент имеет вид 180° ± 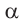
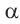
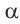
В каждом из обоих случаев, знак полученной в результате преобразования функции имеет одинаковое значение со знаком острого угла 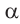
Тригонометрические тождества
Для острого угла 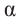
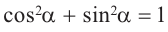
1)Запишите теорему Пифагора:
2)Каждую из сторон равенства разделите на с2:
3)Примените свойство степени:
4) Примите во внимание, что:
Связь между тригонометрическими функциями одного и того же угла
Тождество 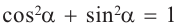
По координатам точки на единичной окружности и по определениям тригонометрических функций имеем:
Для всех значений 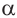
Для всех значений 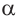
Из данных равенств имеем,что если для угла 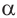
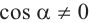
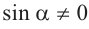
Разделив обе чаете равенства 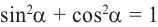
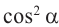
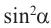
Полученные выше равенства являются тождествами. Их называют основными тригонометрическими тождествами. На основании основных тригонометрических можно написать:
При помощи основных тригонометрических тождеств можно упрощать тригонометрические выражения и вычислять модуль значения всех остальных функций, зная значение одной из них.
Пример 1. Используя основные тригонометрические тождества, докажите,что:
Доказательство:
Пример 2. Зная, что 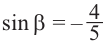
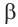
остальные тригонометрические функции.
Из формул 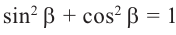
Так как угол 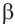
Тогда:
Формулы сложения
Практическая работа .
1)Покажем по шагам, равенство выражения
a)Для значений 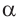
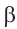
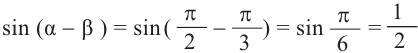
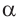
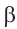
2)Как можно вычислить значение тригонометрических функций для угла 15°, используя разность значений углов 45° и 30°(15° = 45° — 30°)?
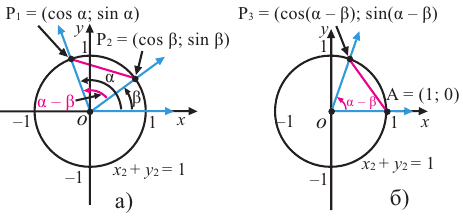
Тригонометрические функции суммы и разности двух углов.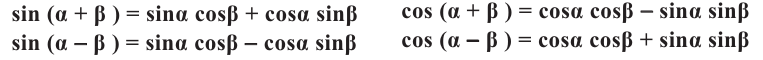

На рисунке
а)для угла 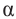
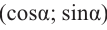
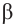
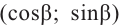
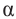
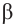
Тогда, для угла 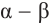
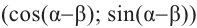
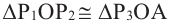
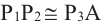

учитывая, что
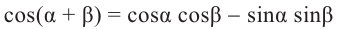

no формулам приведения группируя
no формуле косинуса разности с учётом формул приведения.

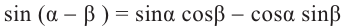
Пример 1. Найдём значение выражения 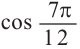
Решение.
Пример 2.
Найдём значение выражения 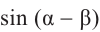
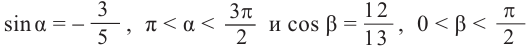
Решение.
Известно что 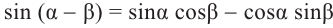
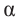
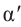
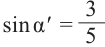
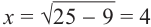
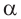
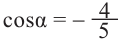
Аналогично, если зная, что 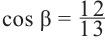
что 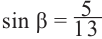
Можно записать формулы сложения для тангенса и котангенса:
no определению no формулам сложения
Аналогичным образом можно показать, что :
Следствия из формул сложения
Практическая работа.
Преобразуйте сумму 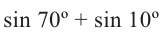
1)
решив систему уравнений найдите такие углы, чтобы их сумма была равна 70°, а разность
2)Запишите следующее 70° = 40° + 30°, 10° = 40° — 30° и упростите
Преобразование суммы(разности) в произведение
Формулы преобразования произведения
Справедливость данных тождеств можно показать при помощи формул сложения:
почленно складываем почленно складываем
Следующее тождество можно доказать аналогичным образом.
Тригонометрические функции двойного аргумента
Формулы сложения позволяют выразить 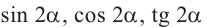
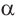
Таким образом, получаем тождества, которые называются формулами двойного аргумента:
Формулы половинного аргумента
Имеем, что
Отсюда: 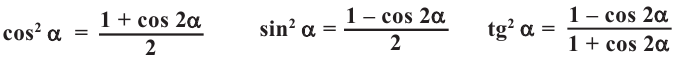
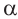
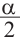
Для половинных аргументов справедливы тождества. 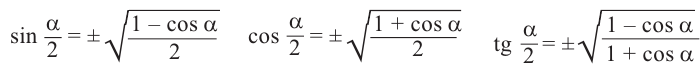
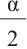
Пример 1. Упростим выражение 
Решение.
Пример 2. He используя калькулятор, вычислим значения 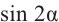
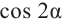

Решение.
Пример 3. Найдём значений 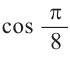
Решение:
Используем формулу половинного аргумента
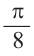
Упрощение тригонометрических выражений
Пример 1. Раскроем скобки и упростим выражение.
Пример 2. Разложим на множители и упростим выражение.
Пример 3. Упростим рациональное выражение, содержащее тригонометрические функции.
Пример 4. Освободим знаменатель от радикала
Здесь 
- Теоремы синусов и косинусов
- Система показательных уравнений
- Непрерывные функции и их свойства
- Правило Лопиталя
- Решение уравнений высших степеней
- Системы неравенств
- Квадратные неравенства
- Точка, прямая и плоскость в пространстве
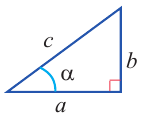
Рассмотрим прямоугольный треугольник ABC.
Синус острого угла прямоугольного треугольника
Отношение противолежащего катета к гипотенузе называют синусом острого угла прямоугольного треугольника.
sin alpha = frac{a}{c}
Косинус острого угла прямоугольного треугольника
Отношение близлежащего катета к гипотенузе называют косинусом острого угла прямоугольного треугольника.
cos alpha = frac{b}{c}
Тангенс острого угла прямоугольного треугольника
Отношение противолежащего катета к близлежащему катету называют тангенсом острого угла прямоугольного треугольника.
tg alpha = frac{a}{b}
Котангенс острого угла прямоугольного треугольника
Отношение близлежащего катета к противолежащему катету называют котангенсом острого угла прямоугольного треугольника.
ctg alpha = frac{b}{a}
Синус произвольного угла
Ордината точки на единичной окружности, которой соответствует угол alpha называют синусом произвольного угла поворота alpha.
sin alpha=y
Косинус произвольного угла
Абсцисса точки на единичной окружности, которой соответствует угол alpha называют косинусом произвольного угла поворота alpha.
cos alpha=x
Тангенс произвольного угла
Отношение синуса произвольного угла поворота alpha к его косинусу называют тангенсом произвольного угла поворота alpha.
tg alpha = y_{A}
tg alpha = frac{sin alpha}{cos alpha}
Котангенс произвольного угла
Отношение косинуса произвольного угла поворота alpha к его синусу называют котангенсом произвольного угла поворота alpha.
ctg alpha =x_{A}
ctg alpha = frac{cos alpha}{sin alpha}
Пример нахождения произвольного угла
Если alpha — некоторый угол AOM, где M — точка единичной окружности, то
sin alpha=y_{M}, cos alpha=x_{M}, tg alpha=frac{y_{M}}{x_{M}}, ctg alpha=frac{x_{M}}{y_{M}}.
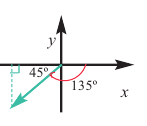
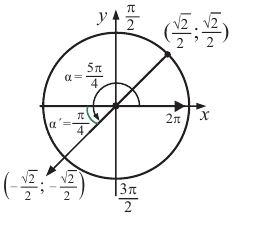
Например, если angle AOM = -frac{pi}{4}, то: ордината точки M равна -frac{sqrt{2}}{2}, абсцисса равна frac{sqrt{2}}{2} и потому
sin left (-frac{pi}{4} right )=-frac{sqrt{2}}{2};
cos left (frac{pi}{4} right )=frac{sqrt{2}}{2};
tg left (-frac{pi}{4} right )=-1;
ctg left (-frac{pi}{4} right )=-1.
Таблица значений синусов косинусов тангенсов котангенсов
Значения основных часто встречающихся углов приведены в таблице:
| 0^{circ} (0) | 30^{circ}left(frac{pi}{6}right) | 45^{circ}left(frac{pi}{4}right) | 60^{circ}left(frac{pi}{3}right) | 90^{circ}left(frac{pi}{2}right) | 180^{circ}left(piright) | 270^{circ}left(frac{3pi}{2}right) | 360^{circ}left(2piright) | |
| sinalpha | 0 | frac12 | frac{sqrt 2}{2} | frac{sqrt 3}{2} | 1 | 0 | −1 | 0 |
| cosalpha | 1 | frac{sqrt 3}{2} | frac{sqrt 2}{2} | frac12 | 0 | −1 | 0 | 1 |
| tg alpha | 0 | frac{sqrt 3}{3} | 1 | sqrt3 | — | 0 | — | 0 |
| ctg alpha | — | sqrt3 | 1 | frac{sqrt 3}{3} | 0 | — | 0 | — |
Синус, косинус, тангенс, котангенс – коротко о главном.
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе
Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому)
Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).
Понятие угла: радиан, градус
Давай для начала разберёмся в понятии угла.
Посмотрим на рисунок.
Вектор ( AB) «повернулся» относительно точки ( A) на некую величину. Так вот мерой этого поворота относительно начального положения и будет выступать угол ( alpha ).
Что же ещё необходимо знать о понятии угла? Ну, конечно же, единицы измерения угла!
Угол, как в геометрии, так и в тригонометрии, может измеряться в градусах и радианах.
Углом в ( 1{}^circ ) (один градус) называют центральный угол в окружности, опирающийся на круговую дугу, равную ( frac{1}{360}) части окружности.
Таким образом, вся окружность состоит из ( 360) «кусочков» круговых дуг. То есть угол, описываемый окружностью, равен ( 360{}^circ ).
То есть на рисунке выше изображён угол ( beta ), равный ( 50{}^circ ), то есть этот угол опирается на круговую дугу размером ( frac{50}{360}) длины окружности.
Углом в ( 1) радиан называют центральный угол в окружности, опирающийся на круговую дугу, длина которой равна радиусу окружности.
Ну что, разобрался? Если нет, то давай разбираться по рисунку.
Итак, на рисунке изображён угол ( gamma ), равный ( 1) радиану.
То есть этот угол опирается на круговую дугу, длина которой равна радиусу окружности (длина ( AB) равна длине ( BB’) или радиус ( r) равен длине дуги ( l)).
Таким образом, длина дуги вычисляется по формуле:
( l=theta cdot r), где ( theta ) – центральный угол в радианах.
Ну что, можешь, зная это, ответить, сколько радиан содержит угол, описываемый окружностью?
Да, для этого надо вспомнить формулу длины окружности. Вот она:
( L=2pi cdot r)
Ну вот, теперь соотнесём эти две формулы и получим, что угол, описываемый окружностью равен ( 2pi ).
То есть, соотнеся величину в градусах и радианах, получаем, что ( 2pi =360{}^circ ).
Соответственно, ( pi =180{}^circ ).
Как можно заметить, в отличие от «градусов», слово «радиан» опускается, так как единица измерения обычно ясна из контекста.
А сколько радиан составляют ( 60{}^circ )?
Всё верно ( frac{pi }{3})!
Уловил? Тогда вперёд закреплять:
( 36{}^circ =?)
( frac{pi }{2}=?)
( 30{}^circ =?)
( frac{pi }{4}=?)
( 90{}^circ =?)
( frac{2pi }{3}=?)
( 45{}^circ =?)
( 20{}^circ =?)
( frac{pi }{6}=?)
( 10{}^circ =?)
( frac{pi }{9}=?)
( 3pi =?)
( 720{}^circ =?)
Возникли трудности?
Тогда смотри ответы:
( frac{pi }{5}; 90{}^circ ;frac{pi }{6};45{}^circ ;frac{pi }{2};120{}^circ ;frac{pi }{4};frac{pi }{9};30{}^circ ;frac{pi }{18};20{}^circ ;540{}^circ ;4pi .)
Cинус, косинус, тангенс, котангенс угла в прямоугольном треугольнике
Итак, с понятием угла разобрались. А что же всё-таки такое синус, косинус, тангенс, котангенс угла?
Давай разбираться. Для этого нам поможет прямоугольный треугольник.
Как называются стороны прямоугольного треугольника?
Всё верно, гипотенуза и катеты.
Гипотенуза – это сторона, которая лежит напротив прямого угла (в нашем примере это сторона ( AC))
Катеты – это две оставшиеся стороны ( AB) и ( BC) (те, что прилегают к прямому углу).
Причём, если рассматривать катеты относительно угла ( angle BAC), то катет ( AB) – это прилежащий катет, а катет ( BC) – противолежащий.
Итак, теперь ответим на вопрос: что такое синус, косинус, тангенс и котангенс угла?
Синус угла – это отношение противолежащего (дальнего) катета к гипотенузе.
В нашем треугольнике ( sin beta =frac{BC}{AC}).
Косинус угла – это отношение прилежащего (близкого) катета к гипотенузе.
В нашем треугольнике ( cos beta =frac{AB}{AC}).
Тангенс угла – это отношение противолежащего (дальнего) катета к прилежащему (близкому).
В нашем треугольнике ( tgbeta =frac{BC}{AB}).
Котангенс угла – это отношение прилежащего (близкого) катета к противолежащему (дальнему).
В нашем треугольнике ( ctgbeta =frac{AB}{BC}).
Эти определения необходимо запомнить!
Чтобы было проще запомнить какой катет на что делить, необходимо чётко осознать, что в тангенсе и котангенсе сидят только катеты, а гипотенуза появляется только в синусе и косинусе.
А дальше можно придумать цепочку ассоциаций. К примеру, вот такую:
Косинус→касаться→прикоснуться→прилежащий;
Котангенс→касаться→прикоснуться→прилежащий.
В первую очередь, необходимо запомнить, что синус, косинус, тангенс и котангенс как отношения сторон треугольника не зависят от длин этих сторон (при одном угле).
Не веришь?
Тогда убедись, посмотрев на рисунок:
Рассмотрим, к примеру, косинус угла ( beta ).
По определению, из треугольника ( ABC): ( cos beta =frac{AB}{AC}=frac{4}{6}=frac{2}{3}).
Но ведь мы можем вычислить косинус угла ( beta ) и из треугольника ( AHI): ( cos beta =frac{AH}{AI}=frac{6}{9}=frac{2}{3}).
Видишь, длины у сторон разные, а значение косинуса одного угла одно и то же. Таким образом, значения синуса, косинуса, тангенса и котангенса зависят исключительно от величины угла.
Если разобрался в определениях, то вперёд закреплять их!
Для треугольника ( ABC), изображённого ниже на рисунке, найдём ( sin alpha , cos alpha , tg alpha , ctg alpha ).
( begin{array}{l}sin alpha =frac{4}{5}=0,8\cos alpha =frac{3}{5}=0,6\tg alpha =frac{4}{3}\ctg alpha =frac{3}{4}=0,75end{array})
Ну что, уловил?
Тогда пробуй сам: посчитай то же самое для угла ( beta ).
Ответы: ( sin beta =0,6; cos beta =0,8; tg beta =0,75; ctg beta =frac{4}{3}).
Единичная (тригонометрическая) окружность
Разбираясь в понятиях градуса и радиана, мы рассматривали окружность с радиусом, равным ( 1).
Такая окружность называется единичной. Еще ее называют тригонометрической. Это одно и тоже.
Эта окружность – универсальная шпаргалка для решения уравнений и даже неравенств, если уметь ей пользоваться!
У нас есть целая статья, посвященная ей, которая так и называется “Тригонометрическая (единичная) окружность”.
Здесь мы тоже ее разберем довольно подробно.
Как можно заметить, данная окружность построена в декартовой системе координат.
Радиус окружности равен единице.
При этом центр окружности лежит в начале координат, начальное положение радиус-вектора зафиксировано вдоль положительного направления оси ( x) (в нашем примере, это радиус ( AB)).
Каждой точке окружности соответствуют два числа: координата по оси ( x) и координата по оси ( y).
А что это за числа-координаты? И вообще, какое отношение они имеют к рассматриваемой теме?
Для этого надо вспомнить про рассмотренный прямоугольный треугольник.
На рисунке, приведённом выше, можно заметить целых два прямоугольных треугольника.
Рассмотрим треугольник ( ACG). Он прямоугольный, так как ( CG) является перпендикуляром к оси ( x).
Чему равен ( cos alpha ) из треугольника ( ACG)?
Всё верно ( cos alpha =frac{AG}{AC}).
Кроме того, нам ведь известно, что ( AC) – это радиус единичной окружности, а значит, ( AC=1).
Подставим это значение в нашу формулу для косинуса. Вот что получается:
( cos alpha =frac{AG}{AC}=frac{AG}{1}=AG).
А чему равен ( sin alpha ) из треугольника ( ACG)?
Ну конечно, ( sin alpha =frac{CG}{AC})!
Подставим значение радиуса ( AC) в эту формулу и получим:
( sin alpha =frac{CG}{AC}=frac{CG}{1}=CG)
Так, а можешь сказать, какие координаты имеет точка ( C), принадлежащая окружности? Ну что, никак?
А если сообразить, что ( cos alpha ) и ( sin alpha ) – это просто числа?
Какой координате соответствует ( cos alpha )?
Ну, конечно, координате ( x)!
А какой координате соответствует ( sin alpha )?
Всё верно, координате ( y)!
Таким образом, точка ( C(x;y)=C(cos alpha ;sin alpha )).
А чему тогда равны ( tg alpha ) и ( ctg alpha )?
Всё верно, воспользуемся соответствующими определениями тангенса и котангенса и получим, что ( tg alpha =frac{sin alpha }{cos alpha }=frac{y}{x}), а ( ctg alpha =frac{cos alpha }{sin alpha }=frac{x}{y}).
А что, если угол будет больше ( 90{}^circ =frac{pi }{2})?
Вот, к примеру, как на этом рисунке:
Что же изменилось в данном примере?
Давай разбираться. Для этого опять обратимся к прямоугольному треугольнику.
Рассмотрим прямоугольный треугольник ( {{A}_{1}}{{C}_{1}}G): угол ( {{C}_{1}}{{A}_{1}}G=180{}^circ -beta ) (как прилежащий к углу ( beta )).
Чему равно значение синуса, косинуса, тангенса и котангенса для угла ( {{C}_{1}}{{A}_{1}}G=180{}^circ -beta )?
Всё верно, придерживаемся соответствующих определений тригонометрических функций:
( begin{array}{l}sin angle {{C}_{1}}{{A}_{1}}G=frac{{{C}_{1}}G}{{{A}_{1}}{{C}_{1}}}=frac{{{C}_{1}}G}{1}={{C}_{1}}G=y;\cos angle {{C}_{1}}{{A}_{1}}G=frac{{{A}_{1}}G}{{{A}_{1}}{{C}_{1}}}=frac{{{A}_{1}}G}{1}={{A}_{1}}G=x;\tgangle {{C}_{1}}{{A}_{1}}G=frac{{{C}_{1}}G}{{{A}_{1}}G}=frac{y}{x};\ctgangle {{C}_{1}}{{A}_{1}}G=frac{{{A}_{1}}G}{{{C}_{1}}G}=frac{x}{y}end{array})
Ну вот, как видишь, значение синуса угла всё так же соответствует координате ( y); значение косинуса угла – координате ( x); а значения тангенса и котангенса соответствующим соотношениям.
Таким образом, эти соотношения применимы к любым поворотам радиус-вектора.
Уже упоминалось, что начальное положение радиус-вектора – вдоль положительного направления оси ( x).
До сих пор мы вращали этот вектор против часовой стрелки, а что будет, если повернуть его по часовой стрелке?
Ничего экстраординарного, получится так же угол определённой величины, но только он будет отрицательным.
Таким образом, при вращении радиус-вектора против часовой стрелки получаются положительные углы, а при вращении по часовой стрелке – отрицательные.
Итак, мы знаем, что целый оборот радиус-вектора по окружности составляет ( 360{}^circ ) или ( 2pi ).
А можно повернуть радиус-вектор на ( 390{}^circ ) или на ( -1140{}^circ )?
Ну конечно, можно!
В первом случае, ( 390{}^circ =360{}^circ +30{}^circ ), таким образом, радиус-вектор совершит один полный оборот и остановится в положении ( 30{}^circ ) или ( frac{pi }{6}).
Во втором случае, ( -1140{}^circ =-360{}^circ cdot 3-60{}^circ ), то есть радиус-вектор совершит три полных оборота и остановится в положении ( -60{}^circ ) или ( -frac{pi }{3}).
Таким образом, из приведённых примеров можем сделать вывод, что углы, отличающиеся на ( 360{}^circ cdot m) или ( 2pi cdot m) (где ( m) – любое целое число), соответствуют одному и тому же положению радиус-вектора.
Ниже на рисунке изображён угол ( beta =-60{}^circ ).
Это же изображение соответствует углу ( -420{}^circ ,-780{}^circ , 300{}^circ ,660{}^circ ) и т.д.
Этот список можно продолжить до бесконечности.
Все эти углы можно записать общей формулой ( beta +360{}^circ cdot m) или ( beta +2pi cdot m) (где ( m) – любое целое число)
( begin{array}{l}-420{}^circ =-60+360cdot (-1);\-780{}^circ =-60+360cdot (-2);\300{}^circ =-60+360cdot 1;\660{}^circ =-60+360cdot 2.end{array})
Теперь, зная определения основных тригонометрических функций и используя единичную окружность, попробуй ответить, чему равны значения:
( begin{array}{l}sin 90{}^circ =?\cos 90{}^circ =?\text{tg} 90{}^circ =?\text{ctg} 90{}^circ =?\sin 180{}^circ =sin pi =?\cos 180{}^circ =cos pi =?\text{tg} 180{}^circ =text{tg} pi =?\text{ctg} 180{}^circ =text{ctg} pi =?\sin 270{}^circ =?\cos 270{}^circ =?\text{tg} 270{}^circ =?\text{ctg} 270{}^circ =?\sin 360{}^circ =?\cos 360{}^circ =?\text{tg} 360{}^circ =?\text{ctg} 360{}^circ =?\sin 450{}^circ =?\cos 450{}^circ =?\text{tg} 450{}^circ =?\text{ctg} 450{}^circ =?end{array})
Вот тебе в помощь единичная окружность:
Возникли трудности? Тогда давай разбираться.
Итак, мы знаем, что:
( begin{array}{l}sin alpha =y;\cosalpha =x;\tgalpha =frac{y}{x};\ctgalpha =frac{x}{y}.end{array})
Отсюда мы определяем координаты точек, соответствующих определённым мерам угла.
Ну что же, начнём по порядку: углу в ( 90{}^circ =frac{pi }{2}) соответствует точка с координатами ( left( 0;1 right)), следовательно:
( sin 90{}^circ =y=1);
( cos 90{}^circ =x=0);
( text{tg} 90{}^circ =frac{y}{x}=frac{1}{0}Rightarrow text{tg} 90{}^circ ) – не существует;
( text{ctg} 90{}^circ =frac{x}{y}=frac{0}{1}=0).
Дальше, придерживаясь той же логики, выясняем, что углам в ( 180{}^circ , 270{}^circ , 360{}^circ , 450{}^circ (=360{}^circ +90{}^circ ) ) соответствуют точки с координатами ( left( -1;0 right),text{ }left( 0;-1 right),text{ }left( 1;0 right),text{ }left( 0;1 right)), соответственно.
Зная это, легко определить значения тригонометрических функций в соответствующих точках. Сначала попробуй сам, а потом сверяйся с ответами.
Ответы:
( displaystyle sin 180{}^circ =sin pi =0)
( displaystyle cos 180{}^circ =cos pi =-1)
( text{tg} 180{}^circ =text{tg} pi =frac{0}{-1}=0)
( text{ctg} 180{}^circ =text{ctg} pi =frac{-1}{0}Rightarrow text{ctg} pi ) – не существует
( sin 270{}^circ =-1)
( cos 270{}^circ =0)
( text{tg} 270{}^circ =frac{-1}{0}Rightarrow text{tg} 270{}^circ ) – не существует
( text{ctg} 270{}^circ =frac{0}{-1}=0)
( sin 360{}^circ =0)
( cos 360{}^circ =1)
( text{tg} 360{}^circ =frac{0}{1}=0)
( text{ctg} 360{}^circ =frac{1}{0}Rightarrow text{ctg} 2pi ) – не существует
( sin 450{}^circ =sin left( 360{}^circ +90{}^circ right)=sin 90{}^circ =1)
( cos 450{}^circ =cos left( 360{}^circ +90{}^circ right)=cos 90{}^circ =0)
( text{tg} 450{}^circ =text{tg} left( 360{}^circ +90{}^circ right)=text{tg} 90{}^circ =frac{1}{0}Rightarrow text{tg} 450{}^circ ) – не существует
( text{ctg} 450{}^circ =text{ctg}left( 360{}^circ +90{}^circ right)=text{ctg} 90{}^circ =frac{0}{1}=0).
Таким образом, мы можем составить следующую табличку:
Нет необходимости помнить все эти значения!
Достаточно помнить соответствие координат точек на единичной окружности и значений тригонометрических функций:
( left. begin{array}{l}sin alpha =y;\cos alpha =x;\tg alpha =frac{y}{x};\ctg alpha =frac{x}{y}.end{array} right} text{Надо запомнить или уметь выводить!!!})
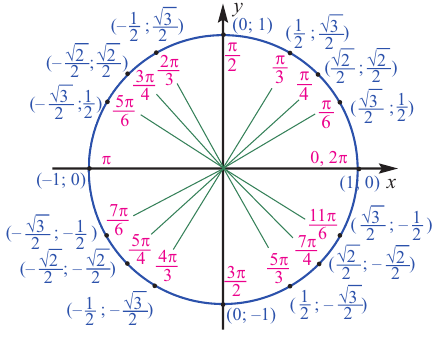
А вот значения тригонометрических функций углов в ( 30{}^circ =frac{pi }{6}, 45{}^circ =frac{pi }{4}) и ( 30{}^circ =frac{pi }{6}, 45{}^circ =frac{pi }{4}), приведённых ниже в таблице, необходимо запомнить:
Не надо пугаться, сейчас покажем один из примеров довольно простого запоминания соответствующих значений:
Координаты точки на окружности
А можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?
Ну, конечно, можно! Давай выведем общую формулу для нахождения координат точки.
Вот, к примеру, перед нами такая окружность:
Нам дано, что точка ( K({{x}_{0}};{{y}_{0}})=K(3;2)) – центр окружности. Радиус окружности равен ( 1,5).
Необходимо найти координаты точки ( P), полученной поворотом точки ( O) на ( delta ) градусов.
Как видно из рисунка, координате ( x) точки ( P) соответствует длина отрезка ( TP=UQ=UK+KQ). Длина отрезка ( UK) соответствует координате ( x) центра окружности, то есть равна ( 3).
Длину отрезка ( KQ) можно выразить, используя определение косинуса:
( cos delta =frac{KQ}{KP}=frac{KQ}{r}Rightarrow KQ=rcdot cos delta ).
Тогда имеем, что для точки ( P) координата ( x={{x}_{0}}+rcdot cos delta =3+1,5cdot cos delta ).
По той же логике находим значение координаты y для точки ( P).
Таким образом,
( y={{y}_{0}}+rcdot sin delta =2+1,5cdot sin delta ).
Итак, в общем виде координаты точек определяются по формулам:
( begin{array}{l}x={{x}_{0}}+rcdot cos delta \y={{y}_{0}}+rcdot sin delta end{array}), где
( {{x}_{0}},{{y}_{0}}) – координаты центра окружности,
( r) – радиус окружности,
( delta ) – угол поворота радиуса вектора.
Как можно заметить, для рассматриваемой нами единичной окружности эти формулы значительно сокращаются, так как координаты центра равны нулю, а радиус равен единице:
( begin{array}{l}x={{x}_{0}}+rcdot cos delta =0+1cdot cos delta =cos delta \y={{y}_{0}}+rcdot sin delta =0+1cdot sin delta =sin delta end{array})
Ну что, попробуем эти формулы на вкус, поупражняясь в нахождении точек на окружности?
Упражнения по нахождению точек на окружности
- Найти координаты точки на единичной окружности, полученной поворотом точки ( Aleft( 1;0 right)) на ( frac{7pi }{3}).
- Найти координаты точки на единичной окружности, полученной поворотом точки ( Aleft( 1;0 right)) на ( 750{}^circ ).
- Найти координаты точки на единичной окружности, полученной поворотом точки ( Aleft( 1;0 right)) на ( -225{}^circ ).
- Точка ( A({{x}_{0}};{{y}_{0}})=A(5;7)) – центр окружности. Радиус окружности равен ( 2). Необходимо найти координаты точки ( P), полученной поворотом начального радиус-вектора на ( -30{}^circ ).
- Точка ( A({{x}_{0}};{{y}_{0}})=A(-7;6)) – центр окружности. Радиус окружности равен ( 3). Необходимо найти координаты точки ( P), полученной поворотом начального радиус-вектора на ( 60{}^circ).
Возникли проблемы в нахождении координат точки на окружности? Реши следующие пять примеров и ты научишься их находить!
Пять примеров нахождения координат точки на окружности
1. Окружность единичная с центром в точке ( left( 0;0 right)), значит, мы можем воспользоваться упрощёнными формулами:
( begin{array}{l}x=cos delta =cos frac{7pi }{3}\y=sin delta =sin frac{7pi }{3}end{array})
Можно заметить, что ( frac{7pi }{3}=frac{6pi +pi }{3}=2pi +frac{pi }{3}). А мы ведь знаем, что ( 2pi ) соответствует полному обороту начальной точки.
Таким образом, искомая точка будет находиться в том же положении, что и при повороте на ( frac{pi }{3}). Зная это, найдём искомые координаты точки:
2. Окружность единичная с центром в точке ( left( 0;0 right)), значит, мы можем воспользоваться упрощёнными формулами:
( begin{array}{l}x=cos delta =cos 750{}^circ \y=sin delta =sin 750{}^circ end{array})
Можно заметить, что ( 750{}^circ =360{}^circ cdot 2+30{}^circ ). Мы знаем, что ( 360{}^circ cdot 2) соответствует двум полным оборотам начальной точки.
Таким образом, искомая точка будет находиться в том же положении, что и при повороте на ( 30{}^circ ).
Зная это, найдём искомые координаты точки:
3. Окружность единичная с центром в точке ( left( 0;0 right)), значит, мы можем воспользоваться упрощёнными формулами:
( begin{array}{l}x=cos beta =cos (-225{}^circ )\y=sin beta =sin (-225{}^circ )end{array}).
Можно заметить, что ( -225{}^circ =-360{}^circ +135{}^circ ; -225{}^circ =-180{}^circ -45{}^circ ).
Изобразим рассматриваемый пример на рисунке:
Радиус ( {{E}_{1}}W) образует с осью ( x) углы, равные ( 45{}^circ) и ( 135{}^circ).
Зная, что табличные значения косинуса и синуса ( 45{}^circ) равны ( displaystyle frac{sqrt{2}}{2}), и определив, что косинус здесь принимает отрицательное значение, а синус положительное, имеем:
4. Для решения данной задачи воспользуемся формулами в общем виде ( begin{array}{l}x={{x}_{0}}+rcdot cos delta \y={{y}_{0}}+rcdot sin delta end{array}), где
( {{x}_{0}},{{y}_{0}}) – координаты центра окружности (в нашем примере, ( {{x}_{0}}=5), ( {{y}_{0}}=7)
( r) – радиус окружности (по условию, ( r=2))
( delta ) – угол поворота радиуса вектора (по условию, ( delta =-30{}^circ ))
Подставим все значения в формулу и получим:
( begin{array}{l}x=5+2cdot cos (-30{}^circ )\y=7+2cdot sin (-30{}^circ )end{array}).
Для определения соответствующих знаков синуса и косинуса построим единичную окружность и угол:
Как можно заметить, значение ( x), то есть ( cos left( -30{}^circ right)) положительно, а значение ( y), то есть ( sin (-30{}^circ )) – отрицательно.
Зная табличные значения соответствующих тригонометрических функций, получаем, что:
5. Для решения данной задачи воспользуемся формулами в общем виде ( begin{array}{l}x={{x}_{0}}+rcdot cos delta \y={{y}_{0}}+rcdot sin delta end{array}), где
( {{x}_{0}},{{y}_{0}}) – координаты центра окружности (в нашем примере, ( {{x}_{0}}=-7), ( {{y}_{0}}=6)
( r) – радиус окружности (по условию, ( r=3))
( delta ) – угол поворота радиуса вектора (по условию, ( delta =60{}^circ )).
( begin{array}{l}x=5+2cdot cos (-30{}^circ )=5+2cdot frac{sqrt{3}}{2}=5+sqrt{3}\y=7+2cdot sin (-30{}^circ )=7+2cdot left( -frac{1}{2} right)=6end{array})
Подставим все значения в формулу и получим:
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук – ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 – WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org – email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж – c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
- отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.
Что такое синус, косинус, тангенс, котангенс
18 мая 2022
Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.
Содержание:
- Ключевые определения: синус, косинус, тангенс, котангенс.
- Почему эти значения зависят только от углов?
- Стандартные углы: 30°, 45°, 60°.
- Простейшие свойства синуса, косинуса, тангенса, котангенса.
- Тригонометрия на координатной сетке.
Никаких сложных формул и длинных решений. Всё расписано максимально подробно. Изучите этот урок — и никаких проблем с тригонометрией не будет. Погнали!
1. Ключевые определения
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Мы видим, что острый угол $alpha $ образован гипотенузой $c$ и катетом $b$. Такой катет будем называть прилежащим. А катет $a$, который не участвует в формировании угла $alpha $, назовём противолежащим:
Это общепринятые названия: как только в прямоугольном треугольнике отмечен острый угол, для него немедленно можно указать прилежащий катет и противолежащий. И тут мы переходим к ключевым определениям.
1.1. Синус, косинус, тангенс, котангенс
Итак, пусть дан прямоугольный треугольник с острым углом $alpha $.
Тогда:
Определение 1. Синус угла $alpha $ — это отношение противолежащего катета к гипотенузе:
[sin alpha =frac{text{противолежащий катет}}{text{гипотенуза}}=frac{a}{c}]
Определение 2. Косинус угла $alpha $ — это отношение прилежащего катета к гипотенузе:
[cos alpha =frac{text{прилежащий катет}}{text{гипотенуза}}=frac{b}{c}]
Определение 3. Тангенс угла $alpha $ — это отношение противолежащего катета к прилежащему:
[operatorname{tg}alpha =frac{text{противолежащий катет}}{text{прилежащий катет}}=frac{a}{b}]
Определение 3. Котангенс угла $alpha $ — это отношение прилежащего катета к противолежащему:
[operatorname{ctg}alpha =frac{text{прилежащий катет}}{text{противолежащий катет}}=frac{b}{a}]
Вот так всё просто! Берём один катет, делим его на гипотенузы (или на другой катет) — и получаем выражение для синуса, косинуса, тангенса и котангенса. Все эти выражения называются тригонометрическими («тригонометрия» = «треугольники измеряю»).
Рассмотрим пару примеров.
Задача 1. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Решение. Это классический прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5. Угол $alpha $ (он же — угол $A$ или угол $BAC$) образован прилежащим катетом $AB=3$гипотенузой $AC=5$. Следовательно катет $BC=4$ — противолежащий.
Имеем:
[begin{align}sin alpha& =frac{BC}{AC}=frac{5}{4} \ cos alpha& =frac{AB}{AC}=frac{3}{5} \ operatorname{tg}alpha& =frac{BC}{AB}=frac{4}{3} end{align}]
Далеко не всегда будут получаться такие красивые ответы. Чаще они будут содержать корни — это следствие теоремы Пифагора. Но важно понимать: как только мы находим длины катетов и гипотенузу, мы сразу можем найти и синусы, косинусы, тангенсы.
Далее в примерах мы не будем считать котангенсы, потому что из формулы котангенса очевидно, что они легко выражаются через тангенсы:
[operatorname{ctg}alpha =frac{1}{operatorname{tg}alpha }]
Но об этом чуть позже.
Задача 2. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Это равнобедренный прямоугольный треугольник с катетами $AB=BC=1$. Найдём гипотенузу по теореме Пифагора:
[begin{align}{{ AC}^{2}} & ={{AB}^{2}}+{{BC}^{2}}=1+1=2 \ AC & =sqrt{2} \ end{align}]
Теперь найдём синус, косинус и тангенс:
[begin{align}sin alpha &=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos alpha &=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}alpha&=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Простое правило, чтобы не запутаться, где прилежащий катет, а где противолежащий. Просто помните: приставка «ко» означает «вместе», «сообща». Поэтому «косинус» — это «катет, лежащий рядом, к гипотенузе», «котангенс» — это «катет, лежащий рядом, к противолежащему». И никак иначе.:)
1.2. Задачи для тренировки
Перед тем как переходить к следующей части урока, предлагаю 4 примера для тренировки.
Задача 3. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{5}{13} \ cos alpha &=frac{12}{13} \ operatorname{tg}alpha &=frac{5}{12} \ end{align}]
Задача 4. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{8}{17} \ cos alpha &=frac{15}{17} \ operatorname{tg}alpha &=frac{8}{15} \ end{align}]
Задача 5. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}}&={{3}^{2}}-{{1}^{2}}=9-1=8 \ l&=sqrt{8}=2sqrt{2} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{3} \ cos alpha&=frac{2sqrt{2}}{3} \ operatorname{tg}alpha&=frac{1}{2sqrt{2}}=frac{sqrt{2}}{4} \ end{align}]
Задача 6. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}} &={{2}^{2}}-{{1}^{2}}=4-1=3 \ l &=sqrt{3} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{2} \ cos alpha&=frac{sqrt{3}}{2} \ operatorname{tg}alpha&=frac{1}{sqrt{3}}=frac{sqrt{3}}{3} \ end{align}]
Как видим, считать синусы, косинусы и тангенсы совсем несложно. Перейдём теперь к принципиально важному вопросу: а зачем вообще всё это нужно?
2. Теорема о единственности
Ключевая идея: синус, косинус, тангенс и котангенс зависят только от величины угла $alpha $ и никак не зависят от прямоугольного треугольника, в котором идут вычисления.
Такого не произойдёт. Потому что есть теорема о единственности.
2.1. Формулировка теоремы
Теорема. Значение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике определяются только величиной этого угла и никак не зависят от самого треугольника.
2.2. Доказательство
Рассмотрим произвольный острый угол $alpha $. Для удобства обозначим его вершину буквой $A$:
А затем впишем в него два произвольных прямоугольных треугольника — $ABC$ и $AMN$. Любым удобным способом. Например, можно вписать эти треугольники вот так:
А можно и вот так — это не имеет никакого значения:
Рассмотрим треугольники $ABC$ и $AMN$. Угол $A$ у них общий; углы [angle ABC=angle AMN=90{}^circ ] по условию. Следовательно, треугольники $ABC$ и $AMN$ подобны по двум углам:
[Delta ABCsim Delta AMN]
Из подобия треугольников следует двойное равенство
[frac{AB}{AM}=frac{BC}{MN}=frac{AC}{AN}]
Выпишем второе равенство — получим пропорцию
[frac{BC}{MN}=frac{AC}{AN}]
Попробуем выразить $sin alpha $. Вспомним основное свойство пропорции: произведение крайних членов равно произведению средних. Поэтому
[BCcdot AN=MNcdot AC]
Разделим обе части равенства на длину каждой гипотенузы — $AN$ и $AC$:
[begin{align}frac{BCcdot AN}{ANcdot AC} &=frac{MNcdot AC}{ANcdot AC} \ frac{BC}{AC} &=frac{MN}{AN} end{align}]
Однако по определению синуса имеем:
[begin{align}sin BAC &=frac{BC}{AC} \ sin MAN &=frac{MN}{AN} \ end{align}]
Получается, что $sin BAC=sin MAN$. Другими словами, вне зависимости от выбора треугольника для данного угла $alpha $ мы всегда будем получать одно и то же значение $sin alpha $.
То же самое касается и $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ — они зависят лишь от градусной меры угла $alpha $ и никак не зависят от конкретного прямоугольного треугольника, в котором они находятся. Теорема доказана.
3. Стандартные углы
Итак, значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ однозначно определяются величиной угла $alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $alpha $ нельзя найти точные значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
- Верно и обратное: для большинства «красивых» $sin alpha $, $cos alpha $ и т.д. нельзя подобрать подходящий угол $alpha $.
Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.
3.1. Три стандартных угла
Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:
[begin{array}{c|ccc} alpha& 30{}^circ& 45{}^circ & 60{}^circ \ hlinesin alpha & frac{1}{2} & frac{sqrt{2}}{2} & frac{sqrt{3}}{2} \ cos alpha & frac{sqrt{3}}{2} & frac{sqrt{2}}{2} & frac{1}{2} \ operatorname{tg}alpha& frac{sqrt{3}}{3} & 1 & sqrt{3} \ end{array}]
Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $alpha =45{}^circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:
Поскольку в равнобедренном треугольнике $angle A=angle B=45{}^circ $, получим:
[begin{align}sin 45{}^circ &=sin A=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos 45{}^circ &=sin A=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}45{}^circ&=sin A=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Это именно те значения, которые указаны в таблице!
Теперь разберёмся с углами $alpha =30{}^circ $ и $alpha =60{}^circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:
Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $angle ABH=angle CBH=30{}^circ $.
Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=sqrt{3}$. Нанесём все данные на чертёж:
Разберёмся с углом 60°:
[begin{align} sin{60}^circ &=sin A=frac{BH}{AB}=frac{sqrt{3}}{2} \ cos{60}^circ&=cos A=frac{AH}{AB}=frac{1}{2} \ operatorname{tg}{60}^circ&=operatorname{tg}A=frac{BH}{AH}=sqrt{3} \ end{align}]
И с углом 30°:
[begin{align} sin{30}^circ &=sin ABH=frac{AH}{AB} =frac{1}{2} \ cos{30}^circ &=cos ABH=frac{BH}{AB} =frac{sqrt{3}}{2} \ operatorname{tg}{30}^circ &=operatorname{tg} ABH=frac{AH}{BH} =frac{1}{sqrt{3}} =frac{sqrt{3}}{3} \ end{align}]
Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!
Возникает вопрос: как быть с другими углами? Например, можно ли найти $sin {50}^circ $? Или, быть может, $cos {10}^circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $alpha $:
[sin alpha =sin A=frac{BC}{AB}=frac{3}{5}=0,6]
Итак, мы знаем синус. Внимание, вопрос: каким должен быть угол $alpha $, чтобы $sin alpha =0,6$? Сколько градусов должно быть в угле $alpha $? Ответ: неизвестно.:)
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $alpha $, чтобы $sin alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:
- Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
- Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.
Ещё раз:
Мы можем посчитать лишь синус, косинус и тангенс для трёх табличных углов.
Например, $sin 30{}^circ $, $cos 45{}^circ $, $operatorname{tg}60{}^circ $ и т.д. А всякие $sin 15{}^circ $, $cos 25{}^circ $ или $operatorname{tg}89,5{}^circ $ — не сможем. По крайней мере пока.:)
И наоборот:
Зная $sin alpha $, $cos alpha $ или $operatorname{tg}alpha $, мы сможем назвать точный угол $alpha $ только в том случае, если все эти синусы, косинусы и тангенсы — среди табличных значений.
Например, мы точно знаем, что если $sin alpha =frac{sqrt{2}}{2}$, то $alpha =45{}^circ $. Но когда $sin alpha =0,6$, мы уже не можем назвать угол $alpha $ (хотя всегда можем построить такой угол).
С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.
4. Свойства синуса, косинуса, тангенса
Мы разберём три ключевых свойства:
- Связь между синусом, косинусом и тангенсом.
- Связь между острыми углами прямоугольного треугольника.
- Основное тригонометрическое тождество.
Свойствам 2 и 3 далее в курсе будут посвящены отдельные уроки. Но основные идеи полезно взять на вооружение уже сейчас.
4.1. Связь между синусом, косинусом и тангенсом
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Выразим синус, косинус:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
А теперь выразим тангенс и заметим, что
[operatorname{tg}alpha =frac{a}{b}=frac{a}{c}cdot frac{c}{b}=frac{sin alpha }{cos alpha }]
Точно так же можно выразить и котангенс:
[operatorname{ctg}alpha =frac{b}{a}=frac{b}{c}cdot frac{c}{a}=frac{cos alpha }{sin alpha }]
Более того, сам тангенс и котангенс тоже связаны:
[operatorname{tg}alpha cdot operatorname{ctg}alpha =frac{a}{b}cdot frac{b}{a}=1]
Мы получили три важнейших тригонометрических формулы:
Основные формулы тригонометрии:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha };quad operatorname{ctg}alpha =frac{cos alpha }{sin alpha };quad operatorname{tg}alpha cdot operatorname{ctg}alpha =1]
Эти формулы нужно знать наизусть. И понимать, откуда они берутся.
4.2. Связь между острыми углами
Рассмотрим прямоугольный треугольник $ABC$, где $angle C=90{}^circ $. Пусть градусная мера $angle A=alpha $ градусов:
Мы помним, что сумма острых углов прямоугольного треугольника равна 90°. Поэтому если $angle A=alpha $, то угол $angle B=90{}^circ -alpha $. Но тогда:
[sin alpha =sin A=frac{BC}{AB}=cos B=cos left( 90{}^circ -alpha right)]
То же самое и с косинусами:
[cos alpha =cos A=frac{AC}{AB}=sin B=sin left( 90{}^circ -alpha right)]
И даже с тангенсами и котангенсами:
[begin{align} operatorname{tg}alpha&=operatorname{tg}A=frac{BC}{AC} =operatorname{ctg}B=operatorname{ctg}left( {90}^circ -alpharight) \ operatorname{ctg}alpha&=operatorname{ctg}A=frac{AC}{BC} = operatorname{tg}B=tgleft( {90}^circ -alpha right) \ end{align}]
Другими словами, если вместо $alpha $ поставить ${90}^circ -alpha $, то исходная тригонометрическая функция поменяется на ко-функцию:
[begin{align}sin left( {90}^circ-alpharight) &=cos alpha \ cos left( {90}^circ-alpharight) &=sin alpha \ operatorname{tg}left( {90}^circ-alpharight) &=operatorname{ctg}alpha\ operatorname{ctg}left( {90}^circ-alpharight) &=operatorname{tg}alphaend{align}]
Но это ещё не всё. Есть гораздо более интересная формула.
4.3. Основное тригонометрическое тождество
Вновь рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Запишем выражения для $sin alpha $ и $cos alpha $:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
Далее заметим, что
[begin{align} {{sin }^{2}}alpha +{{cos }^{2}}alpha&={{left( frac{a}{c} right)}^{2}}+{{left( frac{b}{c} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{c}^{2}}} +frac{{{b}^{2}}}{{{c}^{2}}}= \ & =frac{{{a}^{2}}+{{b}^{2}}}{{{c}^{2}}} end{align}]
В числителе можем применить теорему Пифагора: ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$, поэтому
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =frac{{{c}^{2}}}{{{c}^{2}}}=1]
Правая часть этой формулы вообще не зависит от угла $alpha $.
Основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Это равенство связывает синус и косинус одного и того же угла и верно для всех $alpha $.
С помощью основного тригонометрического тождества можно вычислять косинус, зная синус, и наоборот.
Задача 7. Найдите $18cos alpha $ для острого угла $alpha $, если $sin alpha =frac{sqrt{65}}{9}$.
Решение. Запишем основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Подставим указанное значение $sin alpha $ и выразим $cos alpha $:
[begin{align}{{left( frac{sqrt{65}}{9} right)}^{2}}+{{cos }^{2}}alpha &=1 \ frac{65}{81}+{{cos }^{2}}alpha &=1 \ {{cos }^{2}}alpha &=frac{16}{81} \ cos alpha&=pm frac{4}{9} end{align}]
Поскольку косинус угла в прямоугольном треугольнике не может быть отрицательным, выбираем вариант $cos alpha ={4}/{9};$. Остаётся сделать финальный шаг:
[18cos alpha =18cdot frac{4}{9}=2cdot 4=8]
Вот и всё! Ответ: 8.
В следующем примере мы уже не будем подробно расписывать каждый шаг. Оформим всё так, как надо оформлять на контрольных и экзаменах.
Задача 8. Найдите $48operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{8}{sqrt{113}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-{{left( frac{8}{sqrt{113}} right)}^{2}}= \ & =1-frac{64}{113}=frac{49}{113} \ sin alpha&=pm frac{7}{sqrt{113}} end{align}]
Но ${0}^circ lt alpha lt {90}^circ $, поэтому $sin alpha gt 0$. Следовательно
[sin alpha =frac{7}{sqrt{113}}]
Найдём $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{7}{sqrt{113}}cdot frac{sqrt{113}}{8}=frac{7}{8}]
Окончательный ответ:
[48operatorname{tg}alpha =48cdot frac{7}{8}=6cdot 7=42]
Ответ: 42.
Заметка на будущее: замечание о том, что угол $alpha $ острый, весьма существенно. То, как мы сейчас определяем синусы, косинусы и тангенсы (через прямоугольный треугольник), называется геометрической тригонометрией. Её проходят в 8—9 классе.
Но в 10—11 классах появится алгебраическая тригонометрия, где синусы, косинусы и т.д. вполне могут быть отрицательными. И уже не получится просто так избавиться от минуса.
Но всё это будет чуть позже. А сейчас потренируемся.
Задача 9. ►
Найдите $52cos alpha $ для острого угла $alpha $, если $sin alpha =frac{5}{13}$.
Решение. Найдём $cos alpha $:
[begin{align}{{cos }^{2}}alpha &=1-{{sin }^{2}}alpha = \ &=1-frac{25}{169}=frac{144}{169} \ cos alpha&=pm frac{12}{13} end{align}]
Поскольку $cos alpha gt 0$ для острых $alpha $, выбираем $cos alpha ={12}/{13};$. Итого
[52cos alpha =52cdot frac{12}{13}=48]
Ответ: 48.
Задача 10. ►
Найдите $1+2operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{1}{sqrt{26}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-frac{1}{26}=frac{25}{26} \ sin alpha&=pm frac{5}{sqrt{26}} end{align}]
Поскольку $sin alpha gt 0$ для острых $alpha $, выбираем
[sin alpha =frac{5}{sqrt{26}}]
Считаем $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{5}{sqrt{26}}cdot frac{sqrt{26}}{1}=5]
Откуда
[1+2operatorname{tg}alpha =1+2cdot 5=11]
Ответ: 11.
5. Тригонометрия на координатной сетке
Задачи, которые мы сейчас разберём, вполне могут встретиться в ОГЭ и даже ЕГЭ. Часто в них нет прямоугольного треугольника — есть лишь угол, в который этот треугольник предлагается вписать.
Для решения задач на координатной сетке достаточно посмотреть, через какие узлы сетки проходят интересующие нас лучи. И понять, какие из этих узлов имеет смысл соединить дополнительными построениями.
Звучит страшно, но на практике всё легко.:)
Задача 11. Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение. Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ на луч $BC$.
Треугольник $BAH$ — прямоугольный, причём угол $ABC$ — один из его острых углов. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{3}{4}=0,75]
Это и есть искомый тангенс.
Ответ: 0,75.
Ещё раз: важно, чтобы основание перпендикуляра попадало в узел сетки. Иначе нахождение длины катетов резко усложняется. Попробуйте сами:
Задача 12. ►
Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение.
Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ к лучу $BC$.
Треугольник $BAH$ — прямоугольный с острым углом $ABC$. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{2}{4}=frac{1}{2}]
Ответ: 0,5.
Разумеется, это были совсем простые задачи. Потому что один из лучей был параллелен линиям сетки.
Куда интереснее (и полезнее) рассмотреть ситуации, где лучи направлены под углом к сетке. Суть та же: ищем и соединяем узлы на лучах. Но тут уже нужна наблюдательность.
Задача 13. Найдите тангенс угла $MNK$, изображённого на координатной сетке:
Решение. Луч $KN$ содержит лишь две точки в узлах координатной сетки — собственно, $K$ и $N$. Понятно, что если продолжить луч за точку $K$, мы найдём ещё много таких точек, но будем решать задачу с тем, что есть.
Заметим, что прямая $MN$ наклонена к линиям сетки под углом 45° и образует диагонали квадратов. Это значит, что перпендикуляр к ней тоже будет наклонён под углом 45°.
Дополнительное построение: отрезок $KH$ — диагональ одного из квадратов сетки.
Очевидно, что угол $NHK$ прямой, поэтому треугольник $KHN$ прямоугольный и содержит искомый острый угол $MNK$. Находим тангенс:
[operatorname{tg}MNK=frac{HK}{HN}=frac{sqrt{2}}{2sqrt{2}}=frac{1}{2}=0,5]
Здесь мы предположили, что сторона квадрата сетки равна 1. Но с тем же успехом можно считать, что сторона квадрата $a$:
[operatorname{tg}MNK=frac{HK}{HN}=frac{asqrt{2}}{2asqrt{2}}=frac{1}{2}=0,5]
Ответ: 0,5.
Подобные задачи считаются довольно сложными. По статистике большинство выпускников 9 классов не способны их решать. Но вы-то теперь точно справитесь. Попробуйте:
Задача 14. ►
Найдите тангенс угла $DEF$, изображённого на координатной сетке:
Решение.
Дополнительное построение: отрезок $DH$.
Очевидно, $EH=DH$, угол $EHD$ прямой. Следовательно, треугольник $EDH$ — прямоугольный и равнобедренный. Поэтому $operatorname{tg}DEF=1$.
Либо можно посчитать «напролом», полагая, что сторона квадрата сетки равна $a$:
[operatorname{tg}DEF=frac{asqrt{10}}{asqrt{10}}=1]
Ответ: 1.
Вообще, поиск «правильных» узлов на координатной сетке — это своего рода искусство. И если углубляться в эту тему, то можно быстро выйти на «полуолимпиадные» задачи.
К тому же не существует «самого правильного» дополнительного построения. Задачу на координатной сетке всегда можно решить множеством различных способов. Так, в последнем примере можно было провести перпендикуляр вот так:
И даже так (хотя вряд ли этот способ можно назвать рациональным):
Во всех случаях ответ будет один и тот же. Поэтому не бойтесь экспериментировать. И переходите к следующему уроку — к действительно важным и полезным свойствам синусов, косинусов, тангенсов и котангенсов.:)
Смотрите также:
- Радианная и градусная мера угла
- Как быстро запомнить таблицу синусов и косинусов
- Сложные логарифмические неравенства
- Сложные выражения с дробями. Порядок действий
- Задача B5: площадь фигур с вершиной в начале координат
- Обход точек в стереометрии — 2