СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий
Задания 10. Графики функций. Тригонометрические функции
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 10 № 509123
На рисунке изображён график функции
Найдите a.
Аналоги к заданию № 509123: 509131 509124 509125 509126 509127 509128 509129 509130 509132 509133 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.5 Тригонометрические функции, их графики
Решение
·
·
Сообщить об ошибке · Помощь
2
Тип 10 № 509131
На рисунке изображён график функции
Найдите b.
Аналоги к заданию № 509123: 509131 509124 509125 509126 509127 509128 509129 509130 509132 509133 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.5 Тригонометрические функции, их графики
Решение
·
·
Сообщить об ошибке · Помощь
3
Тип 10 № 509137
На рисунке изображён график функции
Найдите a.
Аналоги к заданию № 509137: 509147 509138 509139 509140 509141 509142 509143 509144 509145 509146 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.5 Тригонометрические функции, их графики
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 10 № 509147
На рисунке изображён график функции
Найдите b.
Аналоги к заданию № 509137: 509147 509138 509139 509140 509141 509142 509143 509144 509145 509146 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.5 Тригонометрические функции, их графики
Решение
·
·
Сообщить об ошибке · Помощь
5
Тип 10 № 509287
На рисунке изображён график функции Найдите a.
Аналоги к заданию № 509287: 509297 509288 509289 509290 509291 509292 509293 509295 509296 509298 … Все
Кодификатор ФИПИ/Решу ЕГЭ: 3.1.5 Преобразования графиков, 3.3.5 Тригонометрические функции, их графики
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
ЕГЭ Профиль №9. Тригонометрические функции
Скачать файл в формате pdf.
ЕГЭ Профиль №9. Тригонометрические функции
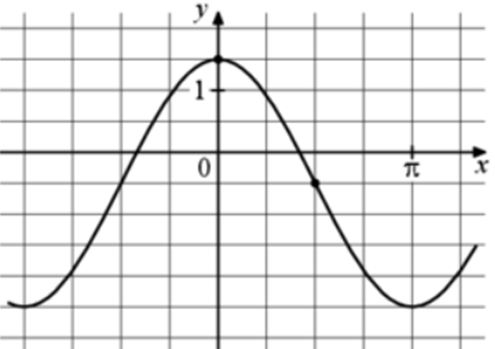
| Задача 1. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a.
Ответ
ОТВЕТ: 2. |
 |
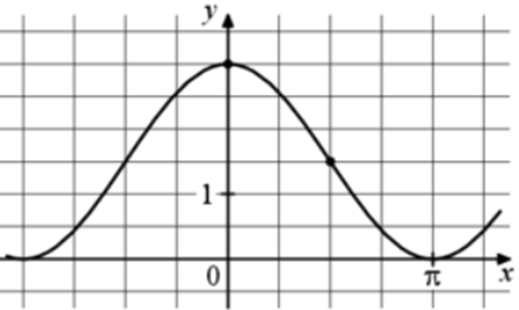
| Задача 2. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a.
Ответ
ОТВЕТ: 1,5. |
 |
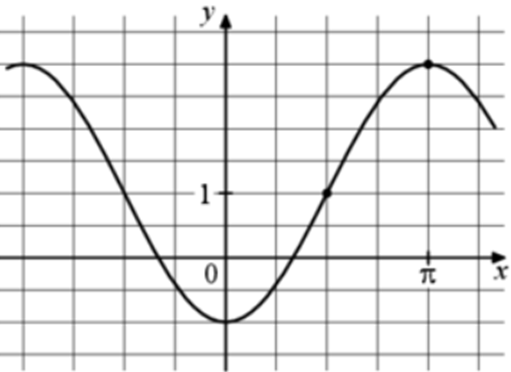
| Задача 3. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a.
Ответ
ОТВЕТ: — 2. |
 |
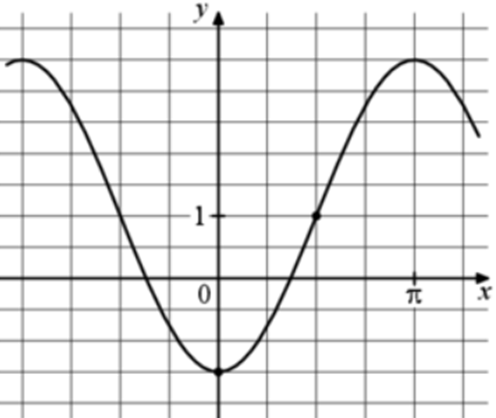
| Задача 4. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a.
Ответ
ОТВЕТ: — 2,5. |
 |
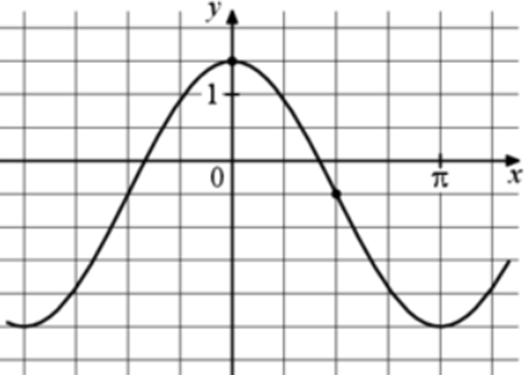
| Задача 5. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b.
Ответ
ОТВЕТ: — 0,5. |
 |
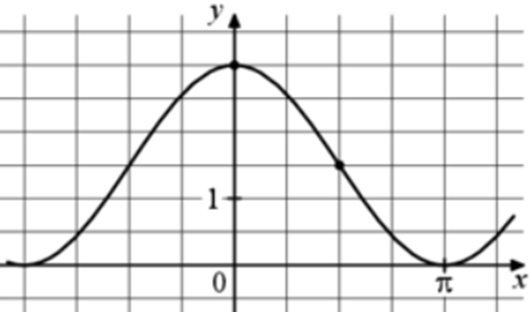
| Задача 6. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b.
Ответ
ОТВЕТ: 1,5. |
 |
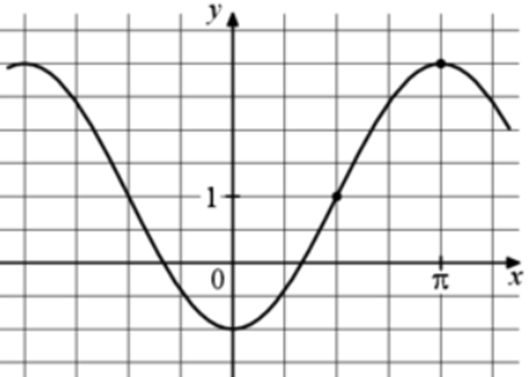
| Задача 7. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b.
Ответ
ОТВЕТ: 1. |
 |
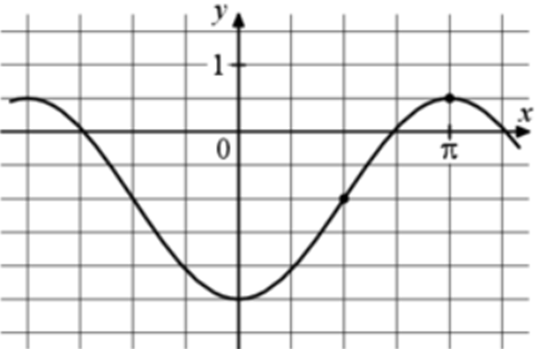
| Задача 8. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b.
Ответ
ОТВЕТ: — 1. |
 |
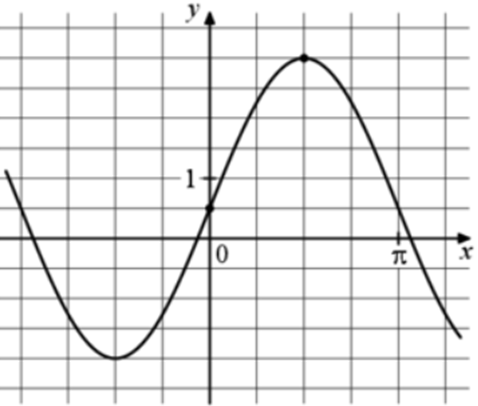
| Задача 9. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a.
Ответ
ОТВЕТ: 2,5. |
 |
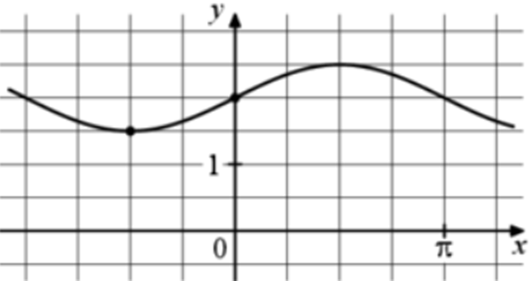
| Задача 10. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a.
Ответ
ОТВЕТ: 0,5. |
 |
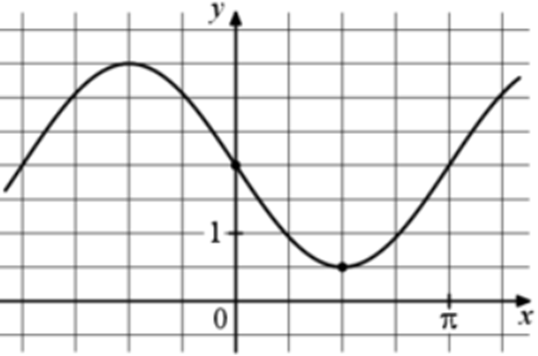
| Задача 11. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a.
Ответ
ОТВЕТ: — 1,5. |
 |
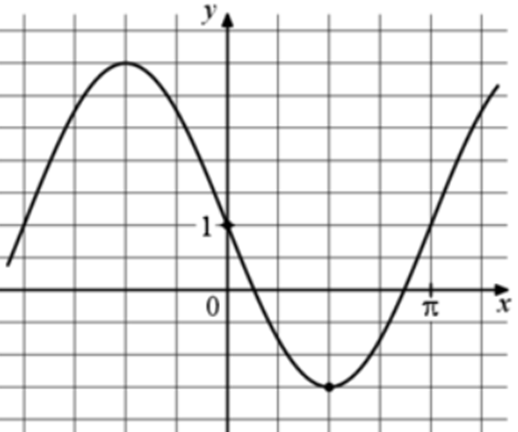
| Задача 12. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a.
Ответ
ОТВЕТ: — 2,5. |
 |
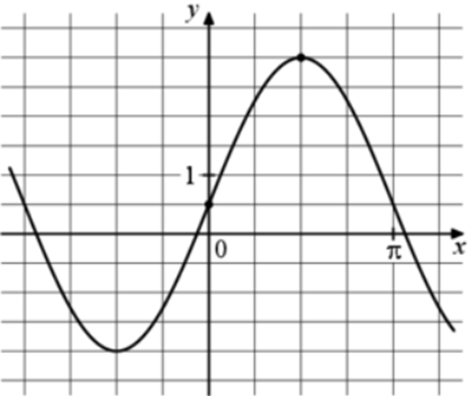
Задача 13. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ
ОТВЕТ: 0,5. |
 |
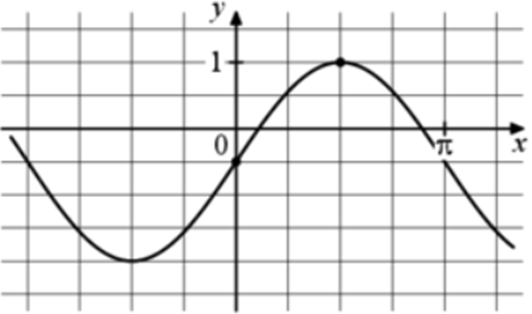
| Задача 14. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b.
Ответ
ОТВЕТ: — 0,5. |
 |
| Задача 15. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b.
Ответ
ОТВЕТ: 0,5. |
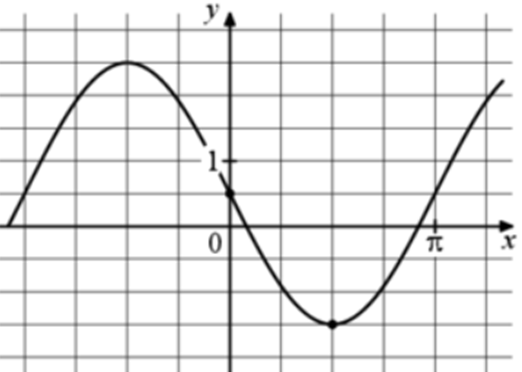 |
| Задача 16. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b.
Ответ
ОТВЕТ: — 0,5. |
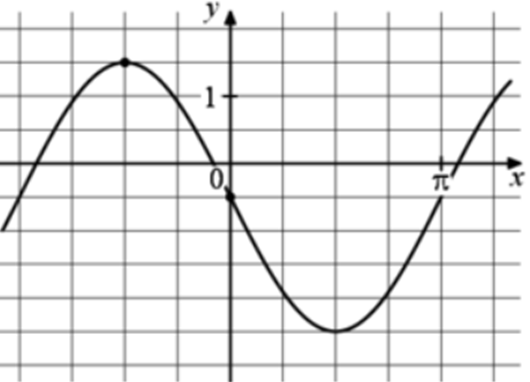 |
| Задача 17. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a.
Ответ
ОТВЕТ: 2. |
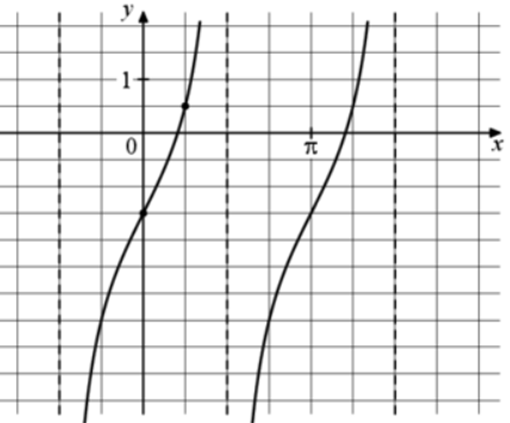 |
| Задача 18. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a.
Ответ
ОТВЕТ: 0,5. |
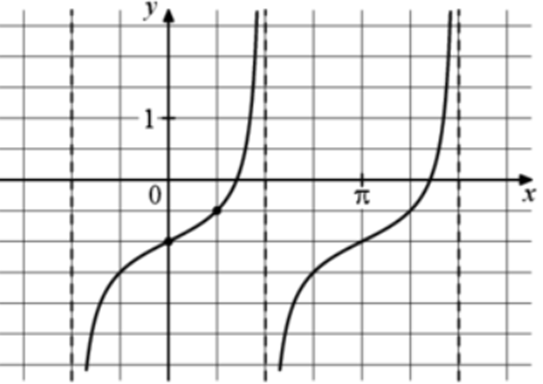 |
| Задача 19. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a.
Ответ
ОТВЕТ: — 2. |
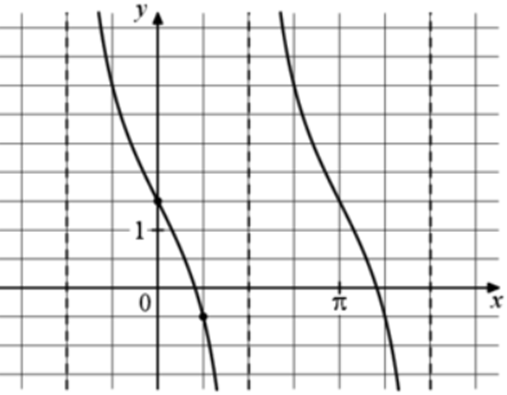 |
| Задача 20. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a.
Ответ
ОТВЕТ: — 0,5. |
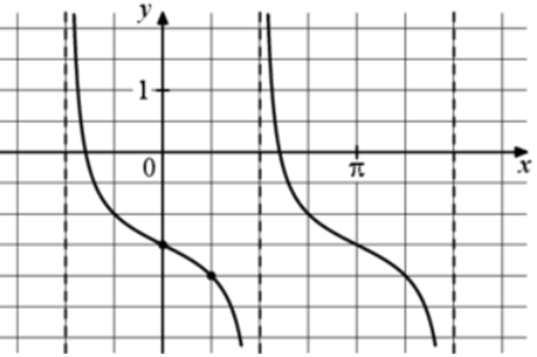 |
| Задача 21. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b.
Ответ
ОТВЕТ: 1. |
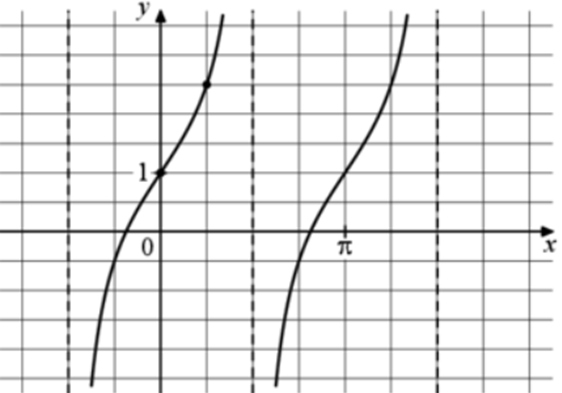 |
| Задача 22. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b.
Ответ
ОТВЕТ: — 1. |
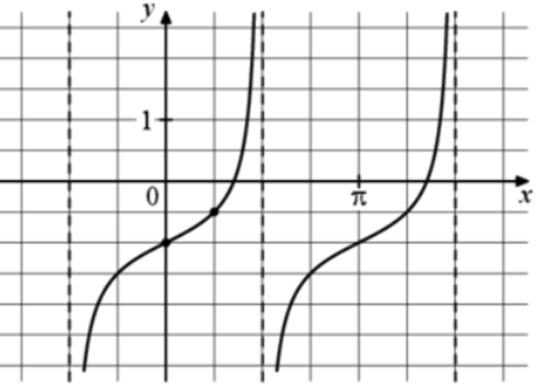 |
| Задача 23. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b.
Ответ
ОТВЕТ: 1,5. |
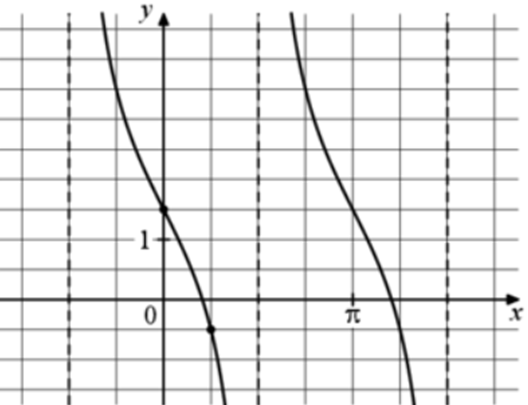 |
| Задача 24. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b.
Ответ
ОТВЕТ: — 1,5. |
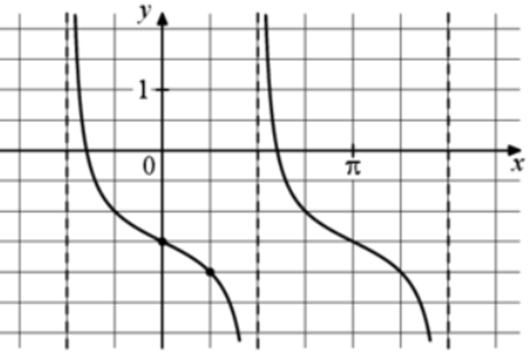 |
Задание
№9 «Графики функции»
ЕГЭ
математика профиль
1) Гиперболы
2) Кусочно-линейная функция
3)Параболы
4) Синусоиды
1) Гиперболы
1. 
где числа a, b и c — целые.
Найдите
Решение.
1. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Асимпто́та, или аси́мптота[1] (от др.-греч. ἀσύμπτωτος — несовпадающая, не касающаяся кривой с бесконечной ветвью) — прямая, обладающая тем свойством, что расстояние от
точки кривой до этой прямой стремится к нулю при удалении точки вдоль
ветви в бесконечность[2]. Термин впервые появился у Аполлония
Пергского, хотя
асимптоты гиперболы исследовал ещё Архимед[3].
2. 
где числа a, b и c — целые.
Найдите
2. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Ответ: −0,75.
3. 
где числа a, b и c — целые.
Найдите
3. 
изображён график функции вида где
числа a, b и c — целые. Найдите
Решение.
График функции имеет горизонтальную асимптоту значит,
График функции имеет вертикальную асимптоту значит,
По графику тогда
Таким образом, Найдём
Ответ: 2,875.
2) Кусочно-линейная функция
1. 
изображён график функции вида где
числа a, b, c и d — целые.
Найдите корень уравнения
1. 
изображён график функции вида где числа a, b, c и d —
целые. Найдите корень уравнения
Решение.

случаев раскрытия модуля получаем линейную функцию где угловой коэффициент
или
а
свободный член или
Очевидно, что
значит, большему значению
углового коэффициента соответствует а
меньшему — Аналогично большему
значению свободного члена соответствует а
меньшему —
По рисунку определяем, что
Значит,
Решим уравнение
Ответ: 1.
2.
На
рисунке изображён график функции вида где
числа a, b, c и d — целые. Найдите
корень уравнения
2. 
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения
Решение.
Заметим, что в точке излома, т.е.
при Значит, корнем уравнения
является число 2.
3. 
где числа a, b, c и d — целые.
Найдите корень уравнения
4. 
где числа a, b, c и d — целые.
Найдите корень уравнения
4. 
изображён график функции вида где числа a, b, c и d — целые.
Найдите корень уравнения
Решение.
Заметим, что в точке излома, т.е.
при Значит, корнем уравнения
является число 3.
3)Параболы

где числа a, b и c —
целые. Найдите значение .
Решение.1 способ
По рисунку определяем, что значит,
Тогда
Решение.2 способ
Выбрать три точки . Например (0;-1),
(6,8), (2;4). Подставив координаты первой точки, мы найдем с=-1. Далее
подставив две другие координаты и с, решаем систему уравнений и находим а и в.
4) Синусоиды

изображён график функции вида где числа a, b, c и d — целые.
Найдите
Решение.
По графику
тогда
и
По графику тогда, если
то
— не
имеет целочисленных решений,
если то
Значит, и
Найдём наименьший положительный период функции
Наименьший положительный период функции равен
а по графику наименьший
положительный период равен 2, тогда
Таким образом, Найдём
Ответ: −2.
22
Окт 2013
Категория: Справочные материалыФункции и графики
Графики тригонометрических функций. Синусоида
2013-10-22
2019-09-21
Смешное видео по теме
График функции y=sinx
Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции .
Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.

Переносим все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.
По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.
Нанесенные на координатную плоскость точки подсказывают нам плавную кривую. Это и есть график функции на
Поскольку на тригонометрическом круге значения синуса повторяются через каждый круг (несколько кругов), то не составит труда построить график функции и на всей числовой прямой.
Указанный выше фрагмент графика синуса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :
График функции называется синусоидой. График симметричен относительно начала координат.
График функции y=cosx
Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и
.
Поступим несколько иначе.
Согласно формулам приведения .
Из чего мы делаем вывод, что график функции будет получен смещением графика функции
на
единиц влево.
То есть график функции – это все таже синусоида, но теперь уже, симметричная относительно оси ординат.
Преобразования синусоиды
Приглашаю посмотреть небольшой видеоролик о том, как меняется поведение синусоиды в зависимости от умножения аргумента или функции на некоторое число или от прибавления к аргументу или функции некоторого числа.
Автор: egeMax |
Нет комментариев
Печать страницы
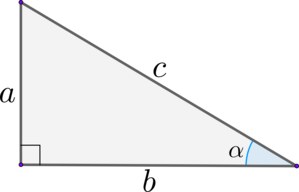
Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
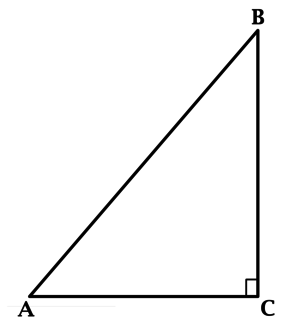
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и
Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .
Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:
Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:
AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.
Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.
Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.
Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB — BH = 18 — 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.
Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.
Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.
Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.
Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:
Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:
Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:
Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:
В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:
A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:
Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:
1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:
Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:
Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:
Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 — = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.
Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
09.03.2023
Теоретическая часть. Тригонометрическая окружность: что, к чему и почему
Друзья, на этой странице представлено видео объяснение простейших вещей, связанных с тригонометрией (с нуля). Чтобы всё было понятно, категорически рекомендуем сначала смотреть всё видео целиком (смотреть всё целиком), а к отдельным его частям вы можете обращаться по ссылкам на этой странице.
Находим синусы и косинусы
Задания, представленные ниже, проще, чем будут на ЕГЭ. Но уверенное решение этих заданий является важным «кирпичиком» для построения навыка решения более сложных заданий. Поэтому предлагаем сначала внимательно разобраться с тем, как найти значения синусов, косинусов, тангенсов и котангенсов основных углов, а затем переходить к решению прототипов ЕГЭ.
| Решаем задания на нахождение синусов и косинусов | Смотреть видео объяснение |
| sin{frac{3pi}{2}} =
Посмотреть ответ |
Смотреть видео объяснение |
| cos{frac{23pi}{6}}=
Посмотреть ответ |
Смотреть видео объяснение |
| sin{frac{323pi}{6}} =
Посмотреть ответ |
Смотреть видео объяснение |
| cos{315^{circ}}=
Посмотреть ответ |
Смотреть видео объяснение |
| sin{660^{circ}}=
Посмотреть ответ |
Смотреть видео объяснение |
| cos{3630^{circ}}=
Посмотреть ответ |
Смотреть видео объяснение |
| sin(-frac{2pi}{3}) =
Посмотреть ответ |
Смотреть видео объяснение |
| cos(-frac{27pi}{4}) =
Посмотреть ответ |
Смотреть видео объяснение |
| sin(-frac{311pi}{3}) =
Посмотреть ответ |
Смотреть видео объяснение |
| cos(-330^{circ}) =
Посмотреть ответ |
Смотреть видео объяснение |
| sin(-675^{circ}) =
Посмотреть ответ |
Смотреть видео объяснение |
| cos(-3645^{circ}) =
Посмотреть ответ |
Смотреть видео объяснение |
Находим тангенсы и котангенсы
| tg frac{pi}{6} =
Посмотреть ответ |
Смотреть видео объяснение |
| ctg frac{29pi}{4} =
Посмотреть ответ |
Смотреть видео объяснение |
| tg frac{323pi}{3} =
Посмотреть ответ |
Смотреть видео объяснение |
| ctg 300^{circ} =
Посмотреть ответ |
Смотреть видео объяснение |
| tg 690^{circ} =
Посмотреть ответ |
Смотреть видео объяснение |
| ctg 3660^{circ} =
Посмотреть ответ |
Смотреть видео объяснение |
| tg (-frac{pi}{3}) =
Посмотреть ответ |
Смотреть видео объяснение |
| ctg(-frac{35pi}{6}) =
Посмотреть ответ |
Смотреть видео объяснение |
| tg (-frac{315pi}{4}) =
Посмотреть ответ |
Смотреть видео объяснение |
| ctg (-315^{circ}) =
Посмотреть ответ |
Смотреть видео объяснение |
| tg (-750^{circ}) =
Посмотреть ответ |
Смотреть видео объяснение |
| ctg (-3720^{circ}) =
Посмотреть ответ |
Смотреть видео объяснение |
Решаем простенькие ЕГЭшные примеры из первой части
Домашнее задание (простая тригонометрия)
Потренируйтесь самостоятельно находить значения тригонометрических выражений! Ответы к заданиям даны в таблице.
| 1 | sin{frac{7pi}{6}}=
Посмотреть ответ |
| 2 | cos{frac{35pi}{3}}=
Посмотреть ответ |
| 3 | sin{frac{337pi}{4}}=
Посмотреть ответ |
| 4 | cos(330^{circ})=
Посмотреть ответ |
| 5 | sin(765^{circ})=
Посмотреть ответ |
| 6 | cos(3735^{circ})=
Посмотреть ответ |
| 7 | sin{-frac{3pi}{4}}=
Посмотреть ответ |
| 8 | cos{-frac{35pi}{6}}=
Посмотреть ответ |
| 9 | sin{-frac{319pi}{3}}=
Посмотреть ответ |
| 10 | cos(-300^{circ})=
Посмотреть ответ |
| 11 | sin(-660^{circ})=
Посмотреть ответ |
| 12 | cos(-3630^{circ})=
Посмотреть ответ |
| 13 | tg{frac{pi}{4}}=
Посмотреть ответ |
| 14 | ctg{frac{32pi}{3}}=
Посмотреть ответ |
| 15 | tg{frac{319pi}{6}}=
Посмотреть ответ |
| 16 | ctg(330^{circ})=
Посмотреть ответ |
| 17 | tg(765^{circ})=
Посмотреть ответ |
| 18 | ctg(2735^{circ})=
Посмотреть ответ |
| 19 | tg(-frac{pi}{6})=
Посмотреть ответ |
| 20 | ctg(-frac{31pi}{4})=
Посмотреть ответ |
| 21 | tg(-frac{314pi}{3})=
Посмотреть ответ |
| 22 | ctg(-300^{circ})=
Посмотреть ответ |
| 23 | tg(-690^{circ})=
Посмотреть ответ |
| 24 | ctg(-3660^{circ})=
Посмотреть ответ |
| 25 | Найдите значение выражения 14sin{30^{circ}}cdotcos{120^{circ}}
Посмотреть ответ |
| 26 | Найдите значение выражения 24sqrt{2}cos(-135^{circ})
Посмотреть ответ |
| 27 | Найдите значение выражения 2sqrt{2}tgfrac{pi}{4}sinfrac{pi}{4}
Посмотреть ответ |
6. Геометрия на плоскости (планиметрия). Часть II
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Вычисление синуса, косинуса и тангенса угла треугольника
В прямоугольном треугольнике:
(blacktriangleright) Синус острого угла равен отношению противолежащего катета к гипотенузе: [{large{sin alpha =
dfrac{a}{c}}}]
(blacktriangleright) Косинус острого угла равен отношению прилежащего катета к гипотенузе: [{large{cos alpha =
dfrac{b}{c}}}]
(blacktriangleright) Тангенс острого угла равен отношению противолежащего катета к прилежащему: [{large{mathrm{tg}, alpha
= dfrac{a}{b}}}]
(blacktriangleright) Котангенс острого угла равен отношению прилежащего катета к противолежащему: [{large{mathrm{ctg},
alpha =dfrac{b}{a}}}]
Важные формулы:
[{large{begin{array}{|lcl|} hline sin^2 alpha+cos^2 alpha
=1&qquad& mathrm{tg}, alpha cdot mathrm{ctg}, alpha
=1\ &&\
mathrm{tg}, alpha=dfrac{sin alpha}{cos
alpha}&&mathrm{ctg}, alpha
=dfrac{cos alpha}{sin alpha}\&&\
hline
end{array}}}]
[begin{array}{|c|c|c|c|c|c|}
hline & phantom{000}, 0^circ phantom{000}& phantom{000},
30^circ phantom{000} &
phantom{000}, 45^circ phantom{000} & phantom{000}, 60^circ phantom{000}
& phantom{000}, 90^circ phantom{000}\[1ex]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2 & 1\[1ex]
hline cos & 1 & frac{sqrt3}2&frac{sqrt2}2½ & 0\[1ex]
hline mathrm{tg} & 0 & frac{sqrt3}3&1&sqrt3 & text{не сущ.}\[1ex]
hline mathrm{ctg}& text{не сущ.} &sqrt3&1&frac{sqrt3}3 & 0\[1ex]
hline
end{array}]
Задание
1
#612
Уровень задания: Легче ЕГЭ
В треугольнике (ABC): (angle C = 90^{circ}), (sin {angle BAC} = dfrac{2}{3}). Найдите (AC), если (AB = 6sqrt{5}).
Синус острого угла в прямоугольном треугольнике равен отношению противолежащего этому углу катета к гипотенузе, тогда [dfrac{BC}{AB} = dfrac{2}{3}qquadRightarrowqquad BC = dfrac{2}{3}AB = 4sqrt{5}.]
По теореме Пифагора (AC^2 = AB^2 — BC^2 = 36cdot 5 — 16cdot 5 = 20cdot 5 = 10^2), тогда (AC = 10).
Ответ: 10
Задание
2
#2098
Уровень задания: Равен ЕГЭ
Дан прямоугольный треугольник (ABC), причем (angle C=90^circ). Известно, что (cos angle B=dfrac13), (AB=9). Найдите (BC).
По определению косинуса [cosangle B=dfrac{BC}{AB}=dfrac13 quad
Leftrightarrow quad BC=dfrac13cdot AB=dfrac13cdot 9=3]
Ответ: 3
Задание
3
#2099
Уровень задания: Равен ЕГЭ
Дан треугольник (ABC), причем (angle C=90^circ). Найдите длину его гипотенузы, если (AC=8, cos angle A=dfrac45).
По определению косинуса [cos angle A=dfrac{AC}{AB}=dfrac45
quad Leftrightarrow quad AB=ACcdot dfrac54=10]
Ответ: 10
Задание
4
#3320
Уровень задания: Равен ЕГЭ
Большее основание равнобедренной трапеции равно (34). Боковая сторона равна (14). Синус острого угла равен (dfrac{2sqrt{10}}7). Найдите меньшее основание.

Проведем (BHperp AD). Из (triangle ABH): [dfrac{2sqrt{10}}7=sinangle A=dfrac{BH}{AB}quadRightarrowquad
BH=4sqrt{10}] Тогда по теореме Пифагора [AH=sqrt{14^2-(4sqrt{10})^2}=6] Так как (AH=0,5(AD-BC)), то (BC=AD-2AH=34-12=22).
Ответ: 22
Задание
5
#3305
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=13), (mathrm{tg},angle A=0,2). Найдите (AH).
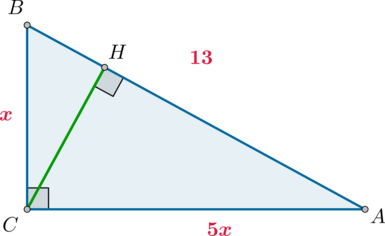
Так как по определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 15] то можно принять (BC=x), (AC=5x). Следовательно, по теореме Пифагора [BC^2+AC^2=AB^2quadRightarrowquad x^2+(5x)^2=13^2quadRightarrowquad
x^2=dfrac{13}2] Из (triangle AHC): [cos angle A=dfrac{AH}{AC}] Из (triangle ABC): [cos angle A=dfrac{AC}{AB}] Следовательно: [dfrac{AH}{AC}=dfrac{AC}{AB}quadRightarrowquad
AH=dfrac{AC^2}{AB}=dfrac{(5x)^2}{13}=dfrac{25}2=12,5]
Ответ: 12,5
Задание
6
#3306
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (CH) – высота, (AB=26), (mathrm{tg},angle B=5). Найдите (AH).
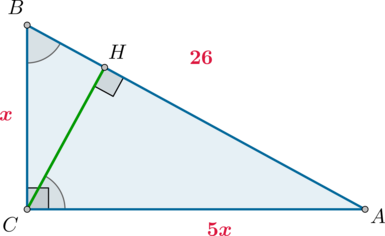
По определению из (triangle ABC): [dfrac{AC}{BC}=mathrm{tg},angle B=dfrac 51] Следовательно, можно принять (AC=5x), (BC=x). Тогда по теореме Пифагора (x^2+(5x)^2=26^2), откуда (x=sqrt{26}).
Тогда [sinangle B=dfrac{AC}{AB}=dfrac5{sqrt{26}}] По свойству прямоугольного треугольника (angle B=angle HCA). Следовательно, из (triangle HCA): [dfrac5{sqrt{26}}=sin angle HCA=dfrac{AH}{AC}quadRightarrowquad
AH=25]
Ответ: 25
Задание
7
#3307
Уровень задания: Равен ЕГЭ
В треугольнике (ABC) угол (C=90^circ), (AB=17), (mathrm{tg},angle A=0,25). Найдите высоту (CH).
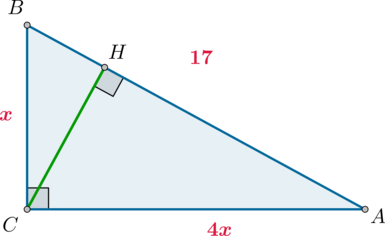
По определению из (triangle ABC): [dfrac{BC}{AC}=mathrm{tg},angle A=dfrac 14] Следовательно, можно принять (AC=4x), (BC=x). Тогда по теореме Пифагора (x^2+(4x)^2=17^2), откуда (x=sqrt{17}).
Так как площадь прямоугольного треугольника (ABC), с одной стороны, равна (0,5CHcdot AB), а с другой стороны, равна (0,5BCcdot AC), то [CHcdot AB=BCcdot ACquadRightarrowquad CH=dfrac{4x^2}{AB}=4]
Ответ: 4
Уметь оперативно и правильно решать задачи ЕГЭ на вычисление элементов многоугольника необходимо всем выпускникам вне зависимости от того, базовый или профильный уровень экзамена они сдают. Причем этой теме традиционно посвящается несколько заданий. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему обязательно стоит уделить внимание задачам, в которых требуется найти синус, косинус и тангенс угла треугольника.
Вместе с образовательным порталом «Школково» вы сможете восполнить пробелы в знаниях и отточить необходимый навык. Весь теоретический и практический материал составлен и изложен таким образом, чтобы все выпускники могли без особых затруднений справляться с задачами ЕГЭ, в которых требуется вычислить тангенс, синус или косинус угла треугольника.
Основные моменты
Первое, что нужно сделать при решении подобных задач в ЕГЭ, — вспомнить, что такое тангенс, косинус и синус угла треугольника. Далее рекомендуется следовать такому алгоритму:
- Выделяем треугольник, в который входит сторона или угол, который требуется найти.
- Определяем известные элементы и выявляем тригонометрическую функцию, которая их связывает.
- Записываем получившееся соотношение и применяем подходящую формулу.
Научившись правильно выполнять упражнения на вычисление элементов многоугольника, а также, например, по теме «Окружность, описанная около многоугольника», которые представлены в данном разделе образовательного портала «Школково», вы сможете закрепить материал и без труда справляться с подобными заданиями на аттестационном экзамене.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ