Тренажер планиметрия егэ - Exhelper.top

Вариант 1 6. Планиметрия

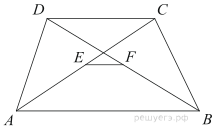
1. Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

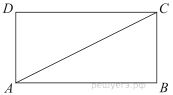
2. Периметр прямоугольника равен 8, а площадь равна 3,5. Найдите диагональ этого прямоугольника.

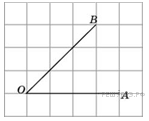
3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2.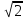

4. Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

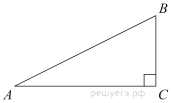
5. Острые углы прямоугольного треугольника равны 53° и 37° . Найдите угол между высотой и медианой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

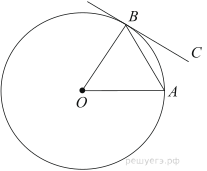
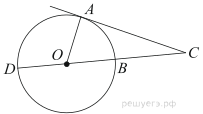
6. Угол между хордой AB и касательной BC к окружности равен 35°. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

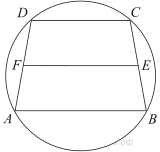
7. Около трапеции описана окружность. Периметр трапеции равен 24, средняя линия равна 11. Найдите боковую сторону трапеции.

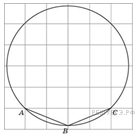
8. Найдите величину угла АВС. Ответ дайте в градусах.

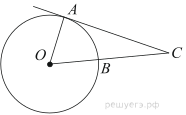
9. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

10. В треугольнике ABC AD — биссектриса, угол C равен 30°, угол BAD равен 22°. Найдите угол ADB. Ответ дайте в градусах.

Вариант 2 6. Планиметрия

В 1. Сторона правильного треугольника равна 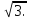Найдите радиус окружности, вписанной в этот треугольник.

2. Две стороны параллелограмма относятся как 9:11, а периметр его равен 40. Найдите большую сторону параллелограмма.

3. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 152°. Ответ дайте в градусах.

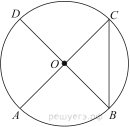
4. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

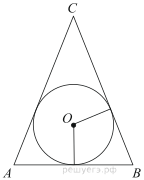
5. Радиус окружности, вписанной в правильный треугольник, равен 44. Найдите высоту этого треугольника.

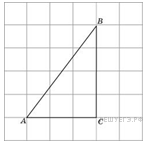
6. Найдите радиус окружности, вписанной в треугольник , считая стороны квадратных клеток равными 1.

7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 9 и 4, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

8. Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

9. Около трапеции описана окружность. Периметр трапеции равен 52, средняя линия равна 21. Найдите боковую сторону трапеции.

10. Радиус окружности, вписанной в правильный треугольник, равен 31. Найдите высоту этого треугольника.

Вариант 3 6. Планиметрия

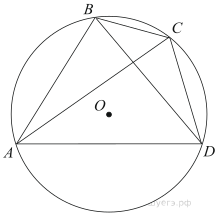
1. Четырехугольник ABCD вписан в окружность. Угол ABC равен 110°, угол ABD равен 70°. Найдите угол CAD. Ответ дайте в градусах.

2. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.

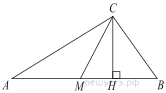
3. В треугольнике АВС АС = ВС = 4 , cos ВАС = 0,25. Найдите высоту АН.

4. В ромбе ABCD угол DAB равен 136°. Найдите угол BDC. Ответ дайте в градусах.

5. В треугольнике АВС угол С равен 90°, СН – высота, АС = 3, cos А = . Найдите ВН.

6. Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

7. В треугольнике ABC угол C равен 90°, CH — высота, BC = 25, BH = 20. Найдите

8. Найдите площадь ромба, если его диагонали равны 4 и 12.

9. В треугольнике АВС АС = ВС = 4, угол С равен 30°. Найдите высоту АН.

10. В треугольнике ABC угол A равен 30°, угол B равен 86°, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE = CB. Найдите угол BDE. Ответ дайте в градусах

Вариант 4 6. Планиметрия

1. В треугольнике ABC угол C равен 90°, CH — высота, АВ = 15, tg А = . Найдите BH.

2. Угол ACB равен 42°. Градусная величина дуги AB окружности, не содержащей точек D и E, равна 124°. Найдите угол DAE. Ответ дайте в градусах.

3. Сторона ромба равна 20, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.

4.Острые углы прямоугольного треугольника равны 24° и 66°. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

5. Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 20°. Найдите меньший угол прямоугольного треугольника.

6. Отрезки AC и BD — диаметры окружности с центром O. Угол AOD равен 66°. Найдите вписанный угол ACB. Ответ дайте в градусах.

7. Катеты равнобедренного прямоугольного треугольника равны 82 + 41

Найдите радиус окружности, вписанной в этот треугольник.

8. В остроугольном треугольнике ABC угол A равен 65°. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

9. В треугольнике АВС угол С равен 90°, СН – высота, ВС = 4, ВН = 4. Найдите

10. Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.

Вариант 5 6. Планиметрия

1. Найдите косинус угла АОВ. В ответе укажите значение косинуса, умноженное на 2.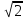

2. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

3. В треугольнике АВС угол С равен 90°, СН — высота, ВС = 3, sin А = . Найдите АН.

4. Хорда AB стягивает дугу окружности в 92°. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

5. Катеты равнобедренного прямоугольного треугольника равны 2+ Найдите радиус окружности, вписанной в этот треугольник.

6. Основания равнобедренной трапеции равны 43 и 7. Высота трапеции равна 27. Найдите тангенс острого угла трапеции.

7. Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

8.Больший угол равнобедренного треугольника равен 98°. Найдите меньший угол. Ответ дайте в градусах.

9. Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

10. Стороны параллелограмма равны 38 и 76. Высота, опущенная на первую сторону, равна 57. Найдите высоту, опущенную на вторую сторону параллелограмма.

Вариант 6 6. Планиметрия

1. Сторона АВ треугольника АВС равна 42. Противолежащий ей угол С равен 150° . Найдите радиус окружности, описанной около этого треугольника.

2. Через концы A, B дуги окружности в 114° проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

3. В треугольнике АВС АС=ВС, АН – высота, АВ=5, sinВАС= . Найдите

4. В треугольнике ABC проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

5. Отрезки AC и BD — диаметры окружности с центром O. Угол ACB равен 38°. Найдите угол AOD. Ответ дайте в градусах.

6. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен Найдите высоту трапеции.

7. В треугольнике ABC угол C равен 90°, АС = 8, cos А = Найдите АВ.

8. Периметр треугольника равен 76, а радиус вписанной окружности равен 8. Найдите площадь этого треугольника.

9. Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

10. В треугольнике ABC угол ACB равен °, угол B равен °, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

Вариант 7 6. Планиметрия

1. Пусть тупым является угол C, тогда сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

2. Две стороны параллелограмма относятся как 3:17, а периметр его равен 40. Найдите большую сторону параллелограмма.

3. В треугольнике ABC AC = BC, AB = 22, tg А = . Найдите AC.

4. Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.

5. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.

6. Найдите площадь треугольника, две стороны которого равны 21 и 2, а угол между ними равен 30°.

7. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

8. Угол ACO равен 35°, где O — центр окружности. Его сторона CA касается окружности. Найдите величину меньшей дуги AB окружности, заключенной внутри этого угла. Ответ дайте в градусах.

9. Угол ACB равен 51°. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 144°. Найдите угол DAE. Ответ дайте в градусах.

10.Боковая сторона равнобедренного треугольника равна 5, угол при вершине, противолежащей основанию, равен 120°. Найдите диаметр описанной окружности этого треугольника.

Вариант 8 6. Планиметрия

1. Два угла вписанного в окружность четырехугольника равны 82° и 58°. Найдите больший из оставшихся углов. Ответ дайте в градусах.

2. Основания равнобедренной трапеции равны 13 и 25, а ее площадь равна 152. Найдите боковую сторону трапеции.

3. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.

4. В треугольнике ABC угол C равен 90°, АС = 17, sin А = . Найдите BC.

5. Площадь треугольника ABC равна 136. DE — средняя линия. Найдите площадь треугольника CDE.

6. В треугольнике ABC AC = BC, AB = 8, tg А = . Найдите AC.

7. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а большая дуга AD окружности, заключенная внутри этого угла, равна 116°. Ответ дайте в градусах.

8. Площадь параллелограмма ABCD равна 176. Точка E — середина стороны CD. Найдите площадь треугольника ADE.

9. Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 47.

10. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на 2

Вариант 9 6. Планиметрия

1. Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 6 и 10.

2. Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

3. Найдите синус угла АОВ. В ответе укажите значение синуса, умноженное на

4. Найдите угол ACO, если его сторона CA касается окружности, O — центр окружности, а меньшая дуга окружности AB, заключенная внутри этого угла, равна 37°. Ответ дайте в градусах.

5. Боковые стороны трапеции, описанной около окружности, равны 27 и 4. Найдите среднюю линию трапеции.

6. В треугольнике АВС АС = ВС, АВ = 7 , tg ВАС = , Найдите высоту

7. Угол между стороной правильного n-угольника, вписанного в окружность, и радиусом этой окружности, проведенным в одну из вершин стороны, равен 80°. Найдите n.

8. Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.

9. Найдите вписанный угол, опирающийся на дугу, которая составляет окружности. Ответ дайте в градусах.

10. Основания равнобедренной трапеции равны 25 и 23. Высота трапеции равна 1. Найдите тангенс острого угла.

Вариант 10 6. Планиметрия

1. Найдите величину угла АВС. Ответ дайте в градусах.

2. В треугольнике ABC угол C равен 76°, AC = BC. Найдите угол A. Ответ дайте в градусах.

3. Площадь треугольника АВС равна 129. ДE – средняя линия, параллельная стороне АВ. Найдите площадь трапеции АВЕД.

4. В треугольнике АВС угол С равен 90°, СН – высота, АН = 12 , cos А = . Найдите АВ.

5. Высота правильного треугольника равна 33. Найдите радиус окружности, описанной около этого треугольника.

6. Основания равнобедренной трапеции равны 5 и 11, а её площадь равна 32. Найдите периметр трапеции.

7. Найдите площадь ромба, если его высота равна 2, а острый угол 30°.

8. Хорда AB делит окружность на две части, градусные величины которых относятся как 3:5. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

9. В треугольнике известно, что , , угол равен 90°. Найдите радиус вписанной окружности.

10. В треугольнике АВС АС = ВС = 27 , — высота, sin ВАС = . Найдите

6. Планиметрия

Вариант 1

Вариант 2

Вариант 3

40
2
7,5
22
17,5
160
0,6
24
2
56

Вариант 4

Вариант 5

2
122
17,5
46
1
1,5
2
41
30
28,5

Вариант 6

Вариант 7

150
17
22
0,8
34
10,5
24
55
21
10

Вариант 8

Вариант 9

24
9
1
53
15,5
4
18
141,75
36
1

Вариант 10

45
52
96,75
27
22
26
8
112,5
4
30

Источник

Здесь размещены материалы из открытого банка ФИПИ, согласно контрольно-измерительных материалов ЕГЭ

Скачать:

Предварительный просмотр:

В треугольнике ABC угол C равен 90∘, CH — высота, AC=25, AH=15. НайдитеcosB.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=5, AH=3. Найдите cosB.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=25, AH=7. Найдите cosB.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=10, AH=Найдите cosB.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=10, AH=. Найдите cosB.
В треугольнике ABC угол C равен 90∘, sinA=0.51. Найдите cosB.
В треугольнике ABC угол C равен 90∘, sinA=0.27. Найдите cosB.
В треугольнике ABC угол C равен 90∘, sinA=0.66. Найдите cosB.
В треугольнике ABC угол C равен 90∘, sinA=0.36. Найдите cosB.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=25, CH=24. НайдитеsinA.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=15, CH=9. Найдите sinA.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=5, CH=. Найдите sinA.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=10, CH=8. Найдите sinA.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=8, BH=4. Найдите sinA.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=25, BH=20. НайдитеcosA.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=4, BH=4. Найдите tgA.
В треугольнике ABC угол C равен 90∘, высота CH равна 20, BC=25. Найдите sinA.
В треугольнике ABC угол C равен 90∘, высота CH равна 4, BC=8. Найдите cosA.
В треугольнике ABC угол C равен 90∘, высота CH равна 4, BC=. Найдите tgA.
В треугольнике ABC угол C равен 90∘, высота CH равна 24, BH=7. Найдите sinA.
В треугольнике ABC угол C равен 90∘, высота CH равна 8, BH=4. Найдите tgA.
В тупоугольном треугольнике ABC AB=BC, AB=25, высота CH равна 15. Найдите косинус угла ABC.
В тупоугольном треугольнике ABC AC=BC=8, высота AH равна 4. Найдите sinACB.
В тупоугольном треугольнике ABC AB=BC, AB=5, высота CH равна 3. Найдите косинус угла ABC.
В тупоугольном треугольнике ABC AB=BC, AB=15, высота CH равна 12. Найдите косинус угла ABC.
В тупоугольном треугольнике ABC AC=BC=25, высота AH равна 20. Найдите cosACB.
В тупоугольном треугольнике ABC AC=BC=4, высота AH равна 4. Найдите tgACB.
В тупоугольном треугольнике ABC AC=BC=8, AH — высота, CH=4. Найдите cosACB.
тупоугольном треугольнике ABC AC=BC=, AH — высота, CH=4. Найдите tgACB.
В тупоугольном треугольнике ABC AC=BC, высота AH равна 7, CH=24. Найдите sinACB.
В тупоугольном треугольнике ABC AC=BC, высота AH равна 24, CH=7. Найдите cosACB.
В тупоугольном треугольнике ABC AC=BC, высота AH равна 4, CH=8. НайдитеtgACB.
В тупоугольном треугольнике ABC AB=BC, AB=15, высота CH равна 12. Найдите косинус угла ABC.
В тупоугольном треугольнике ABC AB=BC, AB=10, высота CH равна . Найдите косинус угла ABC.
В тупоугольном треугольнике ABC AB=BC, AB=5, высота CH равна 2. Найдите косинус угла ABC.
В треугольнике ABC угол C равен 90∘, CH — высота, AH=15, tgA=. НайдитеBH.
В треугольнике ABC угол C равен 90∘, CH — высота, AH=49, tgA=. НайдитеBH.
В треугольнике ABC угол C равен 90∘, CH — высота, AH=6, tgA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AH=8, tgA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AH=27, tgA=. НайдитеBH.
В треугольнике ABC угол C равен 90∘, CH — высота, BH=12, tgA=. НайдитеAH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=10, tgA=3. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=34, tgA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=39, tgA=8. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=39, tgA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=58, tgA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=39, tg=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=26, tgA=8. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=2, tgA=1. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BH=12, sinA=. Найдите AB.
В треугольнике ABC угол C равен 90∘, CH — высота, AH=12, cosA=. Найдите AB
В треугольнике ABC угол C равен 90∘, AB=13, tgA=8. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, AB=51, tgA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, AB=34, tgA=4. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, AB=5, tgA=7. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, AB=5, tgA=3. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, AB=58, tgA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=4, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=2, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=7, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=4, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=5, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=2, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=15, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=15, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=6, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=5, sinA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=10, sinA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=14, sinA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=7, sinA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=5, sinA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=5, sinA=0,2. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=14, sinA=0,5. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=4, sinA=0,5. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=8, sinA=0,25. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=10, sinA=0,3. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=2, sinA=0,5. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=20, sinA=0,2. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=4, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=1, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=7, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=3, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=4, sinA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=2, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=5, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=2, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=15, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=15, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, BC=25, sinA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=10, sinA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=25, sinA=. Найдите высоту CH
В треугольнике ABC угол C равен 90∘, BC=15, sinA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=10, sinA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=25, sinA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=16, sinA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=10, sinA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=20, cosA=0,8. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=12, cosA=0,25. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=20, cosA=0,7. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=4, cosA=0,75. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=10, cosA=0,7. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=20, cosA=0,9. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, BC=20, cosA=0,8. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=7, cosA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=10, cosA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=1, cosA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=7, cosA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=6, cosA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=6, cosA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=12, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=8, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=5, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=5, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=12, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=12, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=, cosA=45. Найдите BH.
В треугольнике ABC AC=BC, AB=30, sinA=0,8. Найдите AC.
В треугольнике ABC AC=BC, AB=6, sinA=0,8. Найдите AC.
В треугольнике ABC AC=BC, AB=14, sinA=0,96. Найдите AC.
В треугольнике ABC AC=BC, AB=2, sinA=0,7. Найдите AC.
В треугольнике ABC AC=BC, AB=8, sinA=0,5. Найдите AC.
В треугольнике ABC AC=BC=4, sinB=. Найдите AB.
В треугольнике ABC AC=BC=25, sinB=. Найдите AB.
В треугольнике ABC AC=BC=25, sinB=. Найдите AB.
В треугольнике ABC AC=BC=15, sinB=. Найдите AB.
В треугольнике ABC AC=BC=5, cosA=0,2. Найдите AB.
В треугольнике ABC AC=BC=14, cosA=0,5. Найдите AB.
В треугольнике ABC AC=BC=4, cosA=0,5. Найдите AB.
В треугольнике ABC AC=BC=20, cosA=0,25. Найдите AB.
В треугольнике ABC AC=BC=20, cosA=0,4. Найдите AB.
В треугольнике ABC AC=BC=20,5, tgA=. Найдите AB.
В треугольнике ABC AC=BC=1,5, tgA=. Найдите AB.
В треугольнике ABC AC=BC=16, tgA=. Найдите AB.
В треугольнике ABC AC=BC=25, tgA=. Найдите AB.
В треугольнике ABC AC=BC=14, tgA=. Найдите AB.
В треугольнике ABC AC=BC=9, tgA=. Найдите AB.
В треугольнике ABC AC=BC=5, tgA=. Найдите AB.
В треугольнике ABC AC=BC, AB=14, sinA=. Найдите AC.
В треугольнике ABC AC=BC, AB=19,2, sinA=. Найдите AC.
В треугольнике ABC AC=BC, AB=9, sinA=. Найдите AC.
В треугольнике ABC AC=BC, AB=32, cosA=0,8. Найдите AC.
В треугольнике ABC AC=BC, AB=6, cosA=0,25. Найдите AC.
В треугольнике ABC AC=BC, AB=28, cosA=0,7. Найдите AC.
В треугольнике ABC AC=BC, AB=24, cosA=0,75. Найдите AC.
В треугольнике ABC AC=BC, AB=30, cosA=0,75. Найдите AC.
В треугольнике ABC AC=BC, AB=22, tgA=. Найдите AC.
В треугольнике ABC AC=BC, AB=24, tgA=. Найдите AC.
В треугольнике ABC AC=BC, AB=12, tgA=. Найдите AC.
В треугольнике ABC AC=BC, AB=32, tgA=. Найдите AC.
В треугольнике ABC AC=BC, AB=14, tgA=. Найдите AC.
В треугольнике ABC AC=BC, AB=24, tgA=. Найдите AC.
В треугольнике ABC AC=BC, AB=3.6, tgA=. Найдите AC.
В треугольнике ABC AC=BC, AB=20, sinBAC=0,8. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=12, sinBAC=0,25. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=20, sinBAC=0,7. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=12, sinBAC=0,5. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=15, sinBAC=0,2. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=10, sinBAC=0,8. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=20, sinBAC=0,75. Найдите высоту AH.
В треугольнике ABC AC=BC, AH — высота, AB=12, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=8, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=5, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=5, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=12, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=12, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=5, cosBAC=0,2. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=20, cosBAC=0,25. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=5, cosBAC=0,4. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=12, cosBAC=0,75. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=20, cosBAC=0,3. НайдитеBH.
В треугольнике ABC AC=BC, AH — высота, AB=10, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=20,5, tgBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=1,5, tgBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=16, tgBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=28, tgBAC=. Найдите BH.
В треугольнике ABC AC=BC, AH — высота, AB=15, tgBAC=. Найдите BH.
В треугольнике ABC AC=BC, AB=25, cosBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=20, cosBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=10, cosBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=30, cosBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=5, cosBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=12, cosBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=22, tgBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=13,6, tgBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=7,8, tgBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=11, tgBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=4,25, tgBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=2,5, tgBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AB=17, tgBAC=. Найдите высоту AH.
В равностороннем треугольнике ABC высота CH равна 2. Найдите AB.

В треугольнике ABC угол C равен 90∘, sinA=0,1. Найдите cosB.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=13, tgA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=13, tgA=5. Найдите BH.
В треугольнике ABC угол C равен 90∘, AB=13, tgA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=10, tgA=3. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=51, tgA=4. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=123, tgA=9. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AB=74, tgA=6. Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=3, sinA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=8, sinA=0,5. Найдите BH.
В треугольнике ABC угол C равен 90∘, BC=5, sinA=. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=3, cosA=. Найдите AH.
В треугольнике ABC угол C равен 90∘, CH — высота, BC=5, cosA=. Найдите BH.
В треугольнике ABC угол C равен 90∘, BC=8, cosA=0,5. Найдите высоту CH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=3, sinA= . Найдите BH.
В треугольнике ABC угол C равен 90∘, CH — высота, AC=3, cosA= . Найдите BH.
В треугольнике ABC AC=BC=8, cosA=0,5. Найдите AB.
В треугольнике ABC AC=BC= 5, cosA=. Найдите AB.
В треугольнике ABC AC=BC= 5, sinA=. Найдите AB.
В треугольнике ABC AC=BC=4, sinBAC=0,25. Найдите высоту AH.
В треугольнике ABC AC=BC=27, AH — высота, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC=4, cosBAC=0,25. Найдите высоту AH.
В треугольнике ABC AC=BC=27, AH — высота, cosBAC=. Найдите BH.
В треугольнике ABC AC=BC, AB=8, cosA=0,5. Найдите AC.
В треугольнике ABC AC=BC=7, tgA= . Найдите AB.
В треугольнике ABC AC=BC, AB=8, tgA= . Найдите AC.
В треугольнике ABC AC=BC, AB=7, tgBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AH — высота, AB=7, tgBAC=. Найдите BH.
В треугольнике ABC AC=BC, AB=8, sinBAC=0,5. Найдите высоту AH.
В треугольнике ABC AC=BC, AH — высота, AB=5, sinBAC=. Найдите BH.
В треугольнике ABC AC=BC, AB=5, cosBAC=. Найдите высоту AH.
В треугольнике ABC AC=BC, AH — высота, AB=8, cosBAC=0,5. Найдите BH.
В параллелограмме ABCD AB=3, AD=21, sinA=. Найдите большую высоту параллелограмма.
Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Основания равнобедренной трапеции равны 43 и 73. Косинус острого угла трапеции равен . Найдите боковую сторону.
Большее основание равнобедренной трапеции равно 34. Боковая сторона равна 14. Синус острого угла равен . Найдите меньшее основание.
Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен . Найдите высоту трапеции.
Меньшее основание равнобедренной трапеции равно 23. Высота трапеции равна 39. Тангенс острого угла равен . Найдите большее основание.
Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
Найдите тангенс угла AOB.

Найдите тангенс угла AOB.

В треугольнике ABC угол C равен 90∘, угол A равен 30∘, AB=2. Найдите высоту CH.

В треугольнике ABC угол C равен 90∘, CH — высота, угол A равен 30∘, AB=2. Найдите AH.

В треугольнике ABC угол C равен 90∘, CH — высота, угол A равен 30∘, AB=4. Найдите BH.

В треугольнике ABC угол C равен 90∘, sinA=, BC=3, CH — высота. Найдите BH.

В треугольнике ABC угол C равен 90∘, sinA=, BC=3. Найдите высоту CH.

В треугольнике ABC угол C равен 90∘, cosA=, BC=3, CH — высота. Найдите AH.

В треугольнике ABC угол C равен 90∘, sinA=, AC=4, CH — высота. Найдите BH.

В треугольнике ABC угол C равен 90∘, угол A равен 60∘, AB= 2. Найдите высоту CH.

В треугольнике ABC угол C равен 90∘, CH — высота, угол A равен 60∘, AB=12. Найдите BH.

В треугольнике ABC AB=BC=AC=2. Найдите высоту CH.

В равностороннем треугольнике ABC высота CH равна 2. Найдите AB.

В треугольнике ABC AC=BC, AB=4, высота CH равна 2. Найдите угол C. Ответ дайте в градусах.

В треугольнике ABC AC=BC=4, угол C равен 30∘. Найдите высоту AH.

В треугольнике ABC AC=BC=6, высота AH равна 3. Найдите угол C. Ответ дайте в градусах.

В треугольнике ABC AC=BC, высота AH равна 4, угол C равен 30∘. Найдите AC.

В треугольнике ABC AC=BC= 6, высота AH равна 3. Найдите градусную меру угла C.

В треугольнике ABC AC=BC, AB=14, AH — высота, BH=7.

Найдите косинус угла BAC.

В треугольнике ABC AC=BC, AB=15, AH — высота, BH=6.

Найдите косинус угла BAC.

В треугольнике ABC AC=BC=2, угол C равен 120∘. Найдите высоту AH.

В треугольнике ABC AC=BC= 2, угол C равен 135∘. Найдите высоту AH.

В треугольнике ABC AC=BC, угол C равен 120∘, AB=2. Найдите AC.

В треугольнике ABC AC=BC, угол C равен 120∘, AC=2. Найдите AB.

В треугольнике ABC угол A равен 38∘, стороны AC и BC равны. Найдите угол C. Ответ дайте в градусах.

В треугольнике ABC угол C равен 118∘, стороны AC и BC равны. Найдите угол A. Ответ дайте в градусах.

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30∘. Боковая сторона треугольника равна 10. Найдите площадь этого треугольника.

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 30∘. Найдите боковую сторону треугольника, если его площадь равна 25.

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150∘. Боковая сторона треугольника равна 20. Найдите площадь этого треугольника.

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен 150∘. Найдите боковую сторону треугольника, если его площадь равна 100.

Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.

В треугольнике ABC угол C равен 90∘, sinA=0.51. Найдите cosB.
В треугольнике ABC угол C равен 90∘, sinA=0.27. Найдите cosB.
В треугольнике ABC угол C равен 90∘, sinA=0.66. Найдите cosB.
В треугольнике ABC угол C равен 90∘, sinA=0.74. Найдите cosB.
В треугольнике ABC угол C равен 90∘, sinA=0.18. Найдите cosB.
В треугольнике ABC AC=BC, AB=6, sinBAC=. Найдите высоту AH.

В треугольнике ABC AC=BC, AB=6, sinBAC=, AH — высота. Найдите BH.

В треугольнике ABC AB=BC, AC=14, высота CH равна 7.

Найдите синус угла ACB.

В треугольнике ABC AC=BC, AB=20, высота AH равна 8.

Найдите синус угла BAC.

В треугольнике ABC AB=BC, AC=6, sinACB=. Найдите высоту CH.

В треугольнике ABC AB=BC, AC=5, cosACB=0,8. Найдите высоту CH.

Найдите площадь треугольника, две стороны которого равны 8 и 12, а угол между ними равен 30∘.

Площадь прямоугольного треугольника равна 24. Один из его катетов на 2 больше другого. Найдите меньший катет.

Площадь треугольника ABC равна 4. DE — средняя линия. Найдите площадь треугольника CDE.

У треугольника со сторонами 9 и 6 проведены высоты к этим сторонам. Высота, проведенная к первой стороне, равна 4. Чему равна высота, проведенная ко второй стороне?

Острый угол прямоугольного треугольника равен 32∘. Найдите острый угол, образованный биссектрисами этого и прямого углов треугольника. Ответ дайте в градусах.

Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите площадь этого треугольника.

В треугольнике ABC угол A равен 40∘, внешний угол при вершине B равен 102∘. Найдите угол C. Ответ дайте в градусах.

В треугольнике ABC стороны AC и BC равны, угол C равен 52∘, угол CBD — внешний. Найдите угол CBD. Ответ дайте в градусах.

В треугольнике ABC стороны AC и BC равны. Внешний угол при вершине B равен 122∘. Найдите угол C. Ответ дайте в градусах.

В треугольнике ABC AB=BC. Внешний угол при вершине B равен 138∘. Найдите угол C. Ответ дайте в градусах.

Один из углов равнобедренного треугольника равен 98∘. Найдите один из других его углов. Ответ дайте в градусах.
В треугольнике ABC угол A равен 30∘, CH — высота, угол BCH равен 22∘. Найдите угол ACB. Ответ дайте в градусах.

В треугольнике ABC угол C равен 50∘, AD — биссектриса, угол CAD равен 28∘. Найдите угол B. Ответ дайте в градусах.

В треугольнике ABC AD — биссектриса, угол C равен 62°, угол CAD равен 31°. Найдите угол B. Ответ дайте в градусах.

В треугольнике ABC угол C равен 30∘, AD — биссектриса, угол BAD равен 22∘. Найдите угол ADB. Ответ дайте в градусах.

В треугольнике ABC проведена биссектриса AD и AB=AD=CD. Найдите меньший угол треугольника ABC. Ответ дайте в градусах.

В треугольнике ABC AC=BC, AD — высота, угол BAD равен 24∘. Найдите угол C. Ответ дайте в градусах.

В треугольнике ABC угол ACB равен 90∘, угол B равен 58∘, CD — медиана. Найдите угол ACD. Ответ дайте в градусах.

В остроугольном треугольнике ABC угол A равен 65∘. BD и CE — высоты, пересекающиеся в точке O. Найдите угол DOE. Ответ дайте в градусах.

В треугольнике ABC угол A равен 56°, углы B и C – острые, высоты BD и CE пересекаются в точке O. Найдите угол DOE. Ответ дайте в градусах.

Два угла треугольника равны 58∘ и 72∘. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.

В треугольнике ABC угол C равен 58∘, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.

Найдите острый угол между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.

В треугольнике ABC CH — высота, AD — биссектриса, O — точка пересечения прямых CH и AD, угол BAD равен 26∘. Найдите угол AOC. Ответ дайте в градусах.

В треугольнике ABC угол A равен 44∘, угол C равен 62∘. На продолжении стороны AB отложен отрезок BD=BC. Найдите угол D треугольника BCD. Ответ дайте в градусах.

Один из углов прямоугольного треугольника равен 29∘. Найдите угол между высотой и биссектрисой, проведёнными из вершины прямого угла. Ответ дайте в градусах.

В прямоугольном треугольнике угол между высотой и биссектрисой, проведенными из вершины прямого угла, равен 21∘. Найдите меньший угол данного треугольника. Ответ дайте в градусах.

Острые углы прямоугольного треугольника равны 24∘ и 66∘. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

В прямоугольном треугольнике угол между высотой и медианой, проведенными из вершины прямого угла, равен 40∘. Найдите больший из острых углов этого треугольника. Ответ дайте в градусах.

Острые углы прямоугольного треугольника равны 24∘ и 66∘. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.

Угол между биссектрисой и медианой прямоугольного треугольника, проведенными из вершины прямого угла, равен 14∘. Найдите меньший угол этого треугольника. Ответ дайте в градусах.

В треугольнике ABC угол B равен 45∘, угол C равен 85∘, AD — биссектриса, E — такая точка на AB, что AE=AC. Найдите угол BDE. Ответ дайте в градусах.

треугольнике ABC угол A равен 30∘, угол B равен 86∘, CD — биссектриса внешнего угла при вершине C, причем точка D лежит на прямой AB. На продолжении стороны AC за точку C выбрана такая точка E, что CE=CB. Найдите угол BDE. Ответ дайте в градусах.

В треугольнике ABC угол A равен 60∘, угол B равен 82∘. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

В треугольнике ABC угол A равен 60∘, угол B равен 82∘. AD, BE и CF — высоты, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.

а рисунке угол 1 равен 46∘, угол 2 равен 30∘, угол 3 равен 44∘. Найдите угол 4. Ответ дайте в градусах.

Боковая сторона равнобедренного треугольника равна 10. Из точки, взятой на основании этого треугольника, проведены две прямые, параллельные боковым сторонам. Найдите периметр получившегося параллелограмма.

В треугольнике ABC угол A равен 60∘, угол B равен 53∘. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
В треугольнике ABC угол A равен 76∘, угол B равен 65∘. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
В треугольнике ABC угол A равен 80∘, угол B равен 68∘. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
В треугольнике ABC угол A равен 13∘, угол B равен 71∘. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
В треугольнике ABC угол A равен 55∘, угол B равен 46∘. AD, BE и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Основания равнобедренной трапеции равны 6 и 12. Боковые стороны равны 5. Найдите синус острого угла трапеции.

Большее основание равнобедренной трапеции равно 12. Боковая сторона равна 5. Синус острого угла равен 0,8. Найдите меньшее основание.

Меньшее основание равнобедренной трапеции равно 6. Высота трапеции равна 10. Тангенс острого угла равен 2. Найдите большее основание.

Основания равнобедренной трапеции равны 6 и 12. Синус острого угла трапеции равен 0,8. Найдите боковую сторону.
Основания равнобедренной трапеции равны 14 и 26, а ее периметр равен 60. Найдите площадь трапеции.

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите периметр трапеции.

Основания равнобедренной трапеции равны 14 и 26, а ее боковые стороны равны 10. Найдите площадь трапеции.

Основания равнобедренной трапеции равны 7 и 13, а ее площадь равна 40. Найдите боковую сторону трапеции.

В равнобедренной трапеции большее основание равно 25, боковая сторона равна 10, угол между ними 60∘. Найдите меньшее основание.

В равнобедренной трапеции основания равны 12 и 27, острый угол равен 60∘. Найдите ее периметр.

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.

Основания равнобедренной трапеции равны 15 и 9, один из углов равен 45∘. Найдите высоту трапеции.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.

Найдите площадь прямоугольной трапеции, основания которой равны 6 и 2, большая боковая сторона составляет с основанием угол 45∘.

Основания прямоугольной трапеции равны 12 и 4. Ее площадь равна 64. Найдите острый угол этой трапеции. Ответ дайте в градусах.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол 150∘. Найдите площадь трапеции.

Основания трапеции равны 27 и 9, боковая сторона равна 8. Площадь трапеции равна 72. Найдите острый угол трапеции, прилежащий к данной боковой стороне. Ответ выразите в градусах.

В треугольнике ABC AD — биссектриса, угол C равен 62°, угол CAD равен 32°. Найдите угол B. Ответ дайте в градусах.

В треугольнике ABC AD — биссектриса, угол C равен 105°, угол CAD равен 7°.Найдите угол B. Ответ дайте в градусах.

В треугольнике ABC AD — биссектриса, угол C равен 104°, угол CAD равен 6°.

Найдите угол B. Ответ дайте в градусах.

В треугольнике ABC AD — биссектриса, угол C равен 104°, угол CAD равен 5°.Найдите угол B. Ответ дайте в градусах.

В треугольнике ABC AD — биссектриса, угол C равен 103°, угол CAD равен 4°.Найдите угол B. Ответ дайте в градусах.

В треугольнике ABC CD — медиана, угол C равен 90°, угол B равен 35°. Найдите угол ACD. Ответ дайте в градусах.

Сторона AB тупоугольного треугольника ABC равна радиусу описанной около него окружности. Найдите угол C. Ответ дайте в градусах.

Чему равен острый вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Найдите хорду, на которую опирается угол 30∘, вписанный в окружность радиуса 3.

Найдите вписанный угол, опирающийся на дугу, которая составляет 15 окружности. Ответ дайте в градусах.

Дуга окружности AC, не содержащая точки B, составляет 200∘. А дуга окружности BC, не содержащая точки A, составляет 80∘. Найдите вписанный угол ACB. Ответ дайте в градусах.

Найдите вписанный угол, опирающийся на дугу, равную окружности. Ответ дайте в градусах.

Чему равен тупой вписанный угол, опирающийся на хорду, равную радиусу окружности? Ответ дайте в градусах.

Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 150∘. Найдите радиус окружности, описанной около этого треугольника.

Радиус окружности равен 1. Найдите величину тупого вписанного угла, опирающегося на хорду, равную . Ответ дайте в градусах.

Найдите хорду, на которую опирается угол 120∘, вписанный в окружность радиуса 3√.

Радиус окружности равен 1. Найдите величину острого вписанного угла, опирающегося на хорду, равную . Ответ дайте в градусах.

Хорда AB делит окружность на две части, градусные величины которых относятся как 5:7. Под каким углом видна эта хорда из точки C, принадлежащей меньшей дуге окружности? Ответ дайте в градусах.

Боковые стороны равнобедренного треугольника равны 40, основание равно 48. Найдите радиус описанной окружности этого треугольника.

Точки A, B, C, расположенные на окружности, делят ее на три дуги, градусные величины которых относятся как 1:3:5. Найдите больший угол треугольника ABC. Ответ дайте в градусах.

AC и BD — диаметры окружности с центром O. Угол ACB равен 38∘. Найдите угол AOD. Ответ дайте в градусах.

В окружности с центром O AC и BD — диаметры. Центральный угол AOD равен 110∘. Найдите вписанный угол ACB. Ответ дайте в градусах.

Угол A четырехугольника ABCD, вписанного в окружность, равен 58∘. Найдите угол C этого четырехугольника. Ответ дайте в градусах.

Стороны четырехугольника ABCD AB, BC, CD и AD стягивают дуги описанной окружности, градусные величины которых равны соответственно 95∘, 49∘, 71∘, 145∘. Найдите угол B этого четырехугольника. Ответ дайте в градусах.

Точки A, B, C, D, расположенные на окружности, делят эту окружность на четыре дуги AB, BC, CD и AD, градусные величины которых относятся соответственно как 4:2:3:6. Найдите угол A четырехугольника ABCD. Ответ дайте в градусах.

Четырехугольник ABCD вписан в окружность. Угол ABC равен 105∘, угол CADравен 35∘. Найдите угол ABD. Ответ дайте в градусах.

Четырехугольник ABCD вписан в окружность. Угол ABD равен 75∘, угол CAD равен35∘. Найдите угол ABC. Ответ дайте в градусах.

Четырехугольник ABCD вписан в окружность. Угол ABC равен 110∘, угол ABDравен 70∘. Найдите угол CAD. Ответ дайте в градусах.

Хорда AB стягивает дугу окружности в 92∘. Найдите угол ABC между этой хордой и касательной к окружности, проведенной через точку B. Ответ дайте в градусах.

Угол между хордой AB и касательной BC к окружности равен 32∘. Найдите величину меньшей дуги, стягиваемой хордой AB. Ответ дайте в градусах.

Через концы A, B дуги окружности в 62∘ проведены касательные AC и BC. Найдите угол ACB. Ответ дайте в градусах.

Касательные CA и CB к окружности образуют угол ACB, равный 122∘. Найдите величину меньшей дуги AB, стягиваемой точками касания. Ответ дайте в градусах.

Угол ACO равен 24∘. Его сторона CA касается окружности. Найдите градусную величину большей дуги AD окружности, заключенной внутри этого угла. Ответ дайте в градусах.

Найдите угол ACB, если вписанные углы ADB и DAE опираются на дуги окружности, градусные меры которых равны соответственно 118∘ и 38∘. Ответ дайте в градусах.

Угол ACB равен 42∘. Градусная мера дуги AB окружности, не содержащей точек D и E, равна 124∘. Найдите угол DAE. Ответ дайте в градусах.

торона правильного треугольника равна 3√. Найдите радиус окружности, описанной около этого треугольника.

Радиус окружности, описанной около правильного треугольника, равен 3√. Найдите сторону этого треугольника.

Высота правильного треугольника равна 3. Найдите радиус окружности, описанной около этого треугольника.

Радиус окружности, описанной около правильного треугольника, равен 3. Найдите высоту этого треугольника.

Гипотенуза прямоугольного треугольника равна 12. Найдите радиус описанной окружности этого треугольника.

Радиус окружности, описанной около прямоугольного треугольника, равен 4. Найдите гипотенузу этого треугольника.

Боковая сторона равнобедренного треугольника равна 1, угол при вершине, противолежащей основанию, равен 120∘. Найдите диаметр описанной окружности этого треугольника.

Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?

Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна 6.

Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту этого треугольника.

Сторона правильного треугольника равна 3√. Найдите радиус окружности, вписанной в этот треугольник.

Радиус окружности, вписанной в правильный треугольник, равен . Найдите сторону этого треугольника.

Сторона ромба равна 1, острый угол равен 30∘. Найдите радиус вписанной окружности этого ромба.

Острый угол ромба равен 30∘. Радиус вписанной в этот ромб окружности равен 2.

Найдите сторону ромба.

Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 3√.

Найдите радиус окружности, вписанной в правильный шестиугольник со стороной 3√.

Сторона AB треугольника ABC равна 1. Противолежащий ей угол C равен 30∘. Найдите радиус окружности, описанной около этого треугольника.

Одна сторона треугольника равна радиусу описанной окружности. Найдите угол треугольника, противолежащий этой стороне. Ответ дайте в градусах.

Угол C треугольника ABC, вписанного в окружность радиуса 3, равен 30∘. Найдите сторону AB этого треугольника.

Около трапеции описана окружность. Периметр трапеции равен 22, средняя линия равна 5. Найдите боковую сторону трапеции.

Боковая сторона равнобедренной трапеции равна ее меньшему основанию, угол при основании равен 60∘, большее основание равно 12. Найдите радиус описанной окружности этой трапеции.

Основания равнобедренной трапеции равны 8 и 6. Радиус описанной окружности равен 5.

Найдите высоту трапеции.

Два угла вписанного в окружность четырехугольника равны 82∘ и 58∘. Найдите больший из оставшихся углов. Ответ дайте в градусах.

Углы A, B и C четырехугольника ABCD относятся как 1:2:3. Найдите угол D, если около данного четырехугольника можно описать окружность. Ответ дайте в градусах.
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 108∘. Найдите число вершин многоугольника.
Периметр правильного шестиугольника равен 72. Найдите диаметр описанной окружности.

Катеты равнобедренного прямоугольного треугольника равны 2+2√. Найдите радиус окружности, вписанной в этот треугольник.

В треугольнике ABC AC=4, BC=3, угол C равен 90∘. Найдите радиус вписанной окружности.

Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите радиус вписанной окружности.

Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Боковые стороны трапеции, описанной около окружности, равны 3 и 5. Найдите среднюю линию трапеции.

Около окружности описана трапеция, периметр которой равен 40. Найдите длину её средней линии.

Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая боковая сторона равна 7. Найдите радиус окружности.

В четырёхугольник ABCD вписана окружность, AB=10, CD=16. Найдите периметр четырёхугольника ABCD.

В четырёхугольник ABCD, периметр которого равен 26, вписана окружность, AB=6. Найдите CD .

В четырехугольник ABCD вписана окружность, AB=10, BC=11 и CD=15. Найдите четвертую сторону четырехугольника.

К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 6, 8, 10. Найдите периметр данного треугольника.

Периметры двух подобных многоугольников относятся как 3:5. Площадь меньшего многоугольника равна 18. Найдите площадь большего многоугольника.

Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.

Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1 : 2.

Периметр прямоугольника равен 34, а площадь равна 60. Найдите диагональ этого прямоугольника.

Середины последовательных сторон прямоугольника, диагональ которого равна 5, соединены отрезками. Найдите периметр образовавшегося четырехугольника.

Во сколько раз площадь квадрата, описанного около окружности, больше площади квадрата, вписанного в эту окружность?

Параллелограмм и прямоугольник имеют одинаковые стороны. Найдите острый угол параллелограмма, если его площадь равна половине площади прямоугольника. Ответ дайте в градусах.

Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма.

Площадь параллелограмма равна 40, две его стороны равны 5 и 10. Найдите большую высоту этого параллелограмма.

Найдите площадь ромба, если его высота равна 2, а острый угол 30∘.

Один угол параллелограмма больше другого на 70∘. Найдите больший угол. Ответ дайте в градусах.

Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.

Две стороны параллелограмма относятся как 3:4, а периметр его равен 70. Найдите большую сторону параллелограмма.

Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении4:3, считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен 88.

Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна 5. Найдите его большую сторону.

Найдите площадь ромба, если его диагонали равны 4 и 12.

Площадь ромба равна 18. Одна из его диагоналей равна 12. Найдите другую диагональ.

Площадь ромба равна 6. Одна из его диагоналей в 3 раза больше другой. Найдите меньшую диагональ.

Найдите высоту ромба, сторона которого равна 3√, а острый угол равен 60∘.

Найдите большую диагональ ромба, сторона которого равна 3√, а острый угол равен 60∘.

Диагонали ромба относятся как 3:4. Периметр ромба равен 200. Найдите высоту ромба.

Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.

Найдите площадь кольца, ограниченного концентрическими окружностями, радиусы которых равны и

Площадь сектора круга радиуса 3 равна 6. Найдите длину его дуги.

Прямая a проходит через точки с координатами (0, 4) и (6, 0). Прямая b проходит через точку с координатами (0, и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Прямая a проходит через точки с координатами (0, 4) и (-6, 0). Прямая b проходит через точку с координатами (0, -6) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

Найдите ординату точки пересечения оси Oy и прямой, проходящей через точку B(6, 4) и параллельной прямой, проходящей через начало координат и точку A(6, 8).

Точки O(0, 0), B(6, 2), C(0, 6) и A являются вершинами параллелограмма. Найдите ординату точки A.

Точки O(0, 0), A(6, 8), C(0, 6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Точки O(0, 0), A(6, 8), B(6, 2) и C являются вершинами параллелограмма. Найдите ординату точки C.

очки O(0, 0), A(10, 8), B(8, 2) и C являются вершинами параллелограмма. Найдите абсциссу точки C.

Точки O(0, 0), A(10, 8), B(8, 2) и C являются вершинами параллелограмма. Найдите ординату точки C.

Точки O(0, 0), B(8, 2), C(2, 6) и A являются вершинами параллелограмма. Найдите ординату точки A.

Точки O (0, 0), A (10, 8), C (2, 6) и B являются вершинами параллелограмма. Найдите абсциссу точки B.

Точки O(0, 0), A(10, 8), C(2, 6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Точки O(0, 0), A(6, 8), B(8, 2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.

Точки O(0, 0), A(10, 0), B(8, 6), C(2, 6) являются вершинами трапеции. Найдите длину ее средней линии DE.

Найдите абсциссу точки пересечения прямой, заданной уравнением 3x+2y=6, с осью Ox.

Найдите ординату точки пересечения прямой, заданной уравнением 3x+2y=6, с осью Oy.

Найдите абсциссу точки пересечения прямых, заданных уравнениями 3x+2y=6 и y=x.

Найдите ординату точки пересечения прямых, заданных уравнениями 3x+2y=6 и y = −x.

Какого радиуса должна быть окружность с центром в точке P(8, 6), чтобы она касалась оси ординат?

Найдите радиус окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (-2, -2), (6, -2), (6, 4), (-2, 4).

Найдите абсциссу центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (-2, -2), (6, -2), (6, 4), (-2, 4).

Найдите ординату центра окружности, описанной около прямоугольника ABCD, вершины которого имеют координаты соответственно (-2, -2), (6, -2), (6, 4), (-2, 4).

Найдите радиус окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6).

Найдите абсциссу центра окружности, описанной около треугольника, вершины которого имеют координаты (8, 0), (0, 6), (8, 6).

Найдите площадь четырехугольника, вершины которого имеют координаты (4, 2), (8, 4), (6, 8), (2, 6).

Найдите площадь треугольника, вершины которого имеют координаты (2;2), (8;10), (8;8).
Найдите площадь трапеции, вершины которой имеют координаты (2, 2), (8, 4), (8, 8), (2, 10).
Найдите площадь трапеции, вершины которой имеют координаты (2, 2), (10, 4), (10, 10), (2, 6).
Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора AO→ + BO→.

Найдите угол между векторами a⃗ и b⃗ . Ответ дайте в градусах.

Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.

Площадь параллелограмма ABCD равна 189. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 153. Найдите площадь параллелограмма A′B′C′D′, вершинами которого являются середины сторон данного параллелограмма.
Площадь параллелограмма ABCD равна 176. Точка E – середина стороны CD. Найдите площадь треугольника ADE.
Площадь треугольника ABC равна 12. DE – средняя линия, параллельная стороне AB. Найдите площадь трапеции ABDE.

По теме: методические разработки, презентации и конспекты

Каталог заданий В1,В2

Материал взят с сайта www.rechuege.ru Дмитрия Гущина и предназначен для отработки заданий на вычисление В1 и В2…

Мне нравится

Источник

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В треугольнике АВС проведена биссектриса АМ. Прямая, проходящая через вершину В перпендикулярно АМ, пересекает сторону АС в точке N. АВ = 6; ВС = 5; АС = 9.

а)  докажите, что биссектриса угла С делит отрезок МN пополам

б)  пусть Р  — точка пересечения биссектрис треугольника АВС. Найдите отношение АР : РN.

Источник: ЕГЭ по математике 19.06.2014. Основная волна, резервная волна. Запад. Вариант 1

Диагональ AC прямоугольника ABCD с центром O образует со стороной AB угол 30°. Точка E лежит вне прямоугольника, причём ∠BEC = 120°.

а)  Докажите, что ∠CBE = ∠COE.

б)  Прямая OE пересекает сторону AD прямоугольника в точке K. Найдите EK, если известно, что BE = 40 и CE  =  24.

Медианы AA₁, BB₁ и CC₁ треугольника ABC пересекаются в точке M. Известно, что AC  =  3MB.

а)  Докажите, что треугольник ABC прямоугольный.

б)  Найдите сумму квадратов медиан AA₁ и CC₁, если известно, что AC = 12.

На сторонах AC и BC треугольника ABC вне треугольника построены квадраты ACDE и BFKC. Точка M  — середина стороны AB.

а)  Докажите, что

б)  Найдите расстояние от точки M до центров квадратов, если AC  =  10, BC  =  32 и ∠ACB  =  30°.

Источник: Типовые тестовые задания по математике, под редакцией И. В. Ященко 2016

На гипотенузу AB прямоугольного треугольника ABC опустили высоту CH. Из точки H на катеты опустили перпендикуляры HK и HE.

а)  Докажите, что точки A, B, K и E лежат на одной окружности.

б)  Найдите радиус этой окружности, если AB = 12, CH = 5.

Пройти тестирование по этим заданиям

Источник

18 июня 2021

В закладки

Обсудить

Жалоба

Тесты по планиметрии

Сборник тестов по всем разделам планиметрии. Проработка этих задач будет служить первым этапом подготовки к успешному решению задачи 16 ЕГЭ. Тесты можно использовать как для работы на спецкурсах по планиметрии, домашней работы, так и итогового контроля.

t1.docx
t2.docx
t3.docx
t4.docx
t5.docx

Автор: Марина Владимировна Авраменко.

Источник

Скачать материал

Сейчас обучается 82 человека из 34 регионов

Сейчас обучается 38 человек из 28 регионов

Сейчас обучается 43 человека из 27 регионов

Описание презентации по отдельным слайдам:

1 слайд

ЕГЭ: планиметрия, параллелограмм(профиль), часть 1
ТП«Анимированная сорбонка с удалением»
2 слайд

Решите задачу и напишите ответ
Площадь прямоугольника равна 18. Найдите его большую сторону, если она на 3 больше меньшей стороны.
Площадь прямоугольника равна произведению его длины на ширину. Пусть одна из сторон прямоугольника равна a, тогда вторая равна a + 3. Поэтому S = a · (a + 3) = 18, получаем a2 + 3a − 18 = 0. Решая квадратное уравнение, получаем, что a = 3. Тогда большая сторона будет равна 6.
1
3 слайд

Решите задачу и напишите ответ
Найдите периметр прямоугольника, если его площадь равна 18, а отношение соседних сторон равно 1:2.
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, тогда вторая равна 2a. Площадь прямоугольника будет соответственно равна S = 2a2 = 18, тогда одна из сторон равна 3, а другая 6. Поэтому P = 2 · 3 + 2 · 6 = 18.
2
4 слайд

Решите задачу и напишите ответ
Периметр прямоугольника равен 42, а площадь 98. Найдите большую сторону прямоугольника.
Площадь прямоугольника равна произведению его длины на ширину. Периметр прямоугольника равен сумме длин всех сторон. Пусть одна из сторон прямоугольника равна a, вторая равна b. Площадь и периметр прямоугольника будут соответственно равны S = a · b = 98, P = 2 · a + 2 · b = 42. Тогда имеем, что большая сторона равна 14.
3
5 слайд

Решите задачу и напишите ответ
Периметр прямоугольника равен 28, а диагональ равна 10. Найдите площадь этого прямоугольника.
Периметр прямоугольника равен сумме длин его сторон. Площадь прямоугольника равна произведению его длины на ширину. Пусть одна из сторон прямоугольника равна a, вторая равна b. Периметр прямоугольника будет соответственно равен P = 2 · a + 2 · b = 28. Диагональ образует в прямоугольнике два прямоугольных треугольника. По теореме Пифагора a2 + b2 = 100. Тогда имеем S = a · b = 48.
4
6 слайд

Решите задачу и напишите ответ
Стороны параллелограмма равны 9 и 15. Высота, опущенная на первую сторону, равна 10. Найдите высоту, опущенную на вторую сторону параллелограмма
Пусть x — искомая высота. Площадь параллелограмма равна произведению его основания на высоту, опущенную на это основание. Вычислим площадь параллелограмма:
S = 9 · 10 = 15 · x.
Из полученного уравнения находим x = 6.
5
7 слайд

Источники:
Шаблон авторский
Автора технологического приема Г.О.Аствацатурова http://didaktor.ru/kak-sdelat-sorbonku-bolee-interaktivnoj
МК №2 Создание анимированной сорбонки с удалением
« Решу ЕГЭ»: математика. ЕГЭ-2019:задания,ответы, решения. Обучающая система Дмитрия Гущина https://math-ege.sdamgia.ru/test?theme=102

Краткое описание документа:

Тренажёр «Решу ЕГЭ: планиметрия, параллелограмм»(профиль), часть 1 предназначен в помощь учителям по организации заинтересованности повторения к занятиям по данной теме при подготовке к итоговой аттестации. Работу можно применить при проведении урока по математике, систематизации, закреплении и проверке знаний учащихся. В презентации использован технологический прием Г.О.Аствацатурова «Анимированные сорбонки с удалением». Для того, чтобы получить решение, надо нажать на сорбонку. Рассмотрены 5 задач с их решения.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 156 856 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

«Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.

Тема

Глава 8. Некоторые сведения из планиметрии

Больше материалов по этой теме

Другие материалы

Тренажёр «Решу ЕГЭ: трапеция, углы»

Учебник: «Геометрия. Учебник 10-11 класс », Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б.
Тема: Глава 8. Некоторые сведения из планиметрии

05.01.2020
241
1

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Основы туризма и гостеприимства»
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
Курс профессиональной переподготовки «Логистика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Этика делового общения»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»
Курс профессиональной переподготовки «Гражданско-правовые дисциплины: теория и методика преподавания в образовательной организации»

Источник

Практика по заданию №15 ЕГЭ по математике базового уровня — планиметрия.

Для выполнения задания №15 необходимо уметь выполнять действия с геометрическими фигурами .

Практика

Источник	Задания
time4math.ru	Скачать задания
math100.ru	Планиметрия

Коды проверяемых элементов содержания (по кодификатору) — 5.1.1–5.1.5, 5.5.1, 5.5.3, 5.5.5

Уровень сложности задания — базовый

Максимальный балл за выполнение задания — 1

Примерное время выполнения задания выпускником, изучавшим математику на базовом уровне (в мин.) — 8

Связанные страницы:

Задание 1 ЕГЭ по математике база — действия с дробями

Задание 2 ЕГЭ по математике база — простейшие текстовые задачи

Задание 3 ЕГЭ по математике база — размеры и единицы измерения

Задание 6 ЕГЭ по математике база — простейшие текстовые задачи

Задание 14 ЕГЭ по математике база — анализ графиков и таблиц

Источник

Геометрия на плоскости (планиметрия)

Задание
1

#199

Уровень задания: Легче ЕГЭ

В треугольнике (ABC): (angle B = 81^{circ}), (angle C = 25^{circ}). Найдите внешний угол при вершине (A). Ответ дайте в градусах.

Согласно теореме о внешнем угле треугольника, (angle B + angle C =) внешнему углу при вершине (A), следовательно (A_{text{внеш}}) ( = 81^{circ} + 25^{circ} = 106^{circ}).

Ответ: 106

Задание
2

#200

Уровень задания: Легче ЕГЭ

В треугольнике (ABC): (angle A = 22^{circ}), внешний угол при вершине (C) равен (130^{circ}). Найдите (angle B). Ответ дайте в градусах.

Согласно теореме о внешнем угле треугольника, (angle A + angle B = C_{text{внеш}}), тогда (22^{circ} + angle B = 130^{circ}), откуда находим (angle B = 130^{circ} — 22^{circ} = 108^{circ}).

Ответ: 108

Задание
3

#201

Уровень задания: Легче ЕГЭ

В треугольнике (ABC): (angle C = 35^{circ}), внешний угол при вершине (B) равен (91^{circ}). Найдите (angle A). Ответ дайте в градусах.

Согласно теореме о внешнем угле треугольника, (angle C + angle A = B_{text{внеш}}), тогда (35^{circ} + angle A = 91^{circ}), откуда находим (angle A = 91^{circ} — 35^{circ} = 56^{circ}).

Ответ: 56

Задание
4

#202

Уровень задания: Легче ЕГЭ

В треугольнике (ABC): (angle C = 70^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.

В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 70^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 70^{circ} — 70^{circ} = 40^{circ}).

Ответ: 40

Задание
5

#203

Уровень задания: Легче ЕГЭ

В треугольнике (ABC): (angle A = 47^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.

В равнобедренном треугольнике углы при основании равны, тогда (angle C = angle A = 47^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 47^{circ} — 47^{circ} = 86^{circ}).

Ответ: 86

Задание
6

#204

Уровень задания: Легче ЕГЭ

В треугольнике (ABC): (angle C = 36^{circ}), (AB = BC). Найдите (angle B). Ответ дайте в градусах.

В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C = 36^{circ}). Так как у любого треугольника сумма углов равна (180^{circ}), то (angle B = 180^{circ} — 36^{circ} — 36^{circ} = 108^{circ}).

Ответ: 108

Задание
7

#205

Уровень задания: Легче ЕГЭ

В треугольнике (ABC): (angle B = 38^{circ}), (AB = BC). Найдите (angle C). Ответ дайте в градусах.

В равнобедренном треугольнике углы при основании равны, тогда (angle A = angle C). Так как у любого треугольника сумма углов равна (180^{circ}), то (180^{circ} = 38^{circ} + angle A + angle C = 38^{circ} + 2cdot angle A), откуда (2cdot angle A = 142^{circ}), тогда (angle A = 71^{circ}).

Ответ: 71

Источник

Скачать:

Предварительный просмотр:

По теме: методические разработки, презентации и конспекты

Каталог заданий В1,В2

Тесты по планиметрии

Описание презентации по отдельным слайдам:

Краткое описание документа:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Тема

Другие материалы

Вам будут интересны эти курсы:

Геометрия на плоскости (планиметрия)

Новое и интересное на сайте: