Тренажер стереометрия егэ - Exhelper.top

По теме: методические разработки, презентации и конспекты

Решение стереометрической задачи тремя различными способами

Здесь представлено на трех файлах моё решение решение задачи С2 (вариант 13) из пособия «МАТЕМАТИКА. Подготовка к ЕГЭ-2011» под редакцией Ф.Ф. Лысенко, С.Ю. Калабухова. Эта-же задача встречается в пос…

Методическая разработка по теме: «Применение аналитической геометрии к решению стереометрических задач».

ВЫЧИСЛЕНИЕ РАССТОЯНИЙ И УГЛОВ Рассмотрим несколько геометрических задач, для решения которых необходимо вычислить те или иные расстояния или углы в пространст…

Тема 36. ГЕОМЕТРИЯ.ОСНОВНЫЕ СВЕДЕНИЯ ДЛЯ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ.

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э…

Тема 37.ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 34-36: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ И СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ»

Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к государственной итоговой аттестации (ГИА) и единому государственному экзамену (ЕГЭ) по математике, …

Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»

Учёные всегда стремились упростить себе жизнь – придумывали новые, простые методы решения, универсальные для множества задач, позволяющие быстро решить даже самую трудную задачу. …

Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»

Программа внеурочной деятельности «Практикум решения стереометрических задач». Пропедевтика стереометрических знаний на примере качественных стереометрических задач.

Всем известная трудность в изучении стереометрии, возникающая у учащихся 10 классов, в значительной степени объясняется низким уровнем развитием их пространственных представлений. Ученики теряю…

Источник

Тренажёр по геометрии. Стереометрия в задачах ЕГЭ.

Тест предназначен для учащихся 11 классов для проверки уровня подготовки к государственной итоговой аттестации по геометрии, в нём содержатся задачи по разделу «Стереометрия». В тесте 9 задач из Открытого банка. Ответом для каждого задания служит целое число или десятичная дробь.

Для подготовки к ЕГЭ.

Работа предназначена для закрепления знаний по стереометрии. Состоит из 9 заданий. Ответом для каждого задания служит целое число или десятичная дробь. Желаю удачи!

Количество вопросов в тесте:
9

Источник

Вариант 1 8. Стереометрия

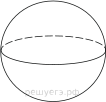
1.Площадь большого круга шара равна 3. Найдите площадь поверхности шара.

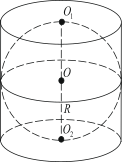
2. Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

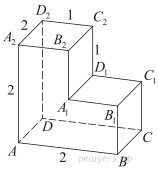
3. Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

4. Площадь боковой поверхности цилиндра равна , а диаметр основания — 8. Найдите высоту цилиндра.

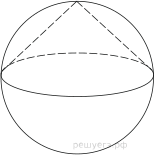
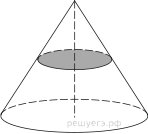
5. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.

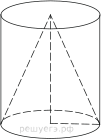
6. Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

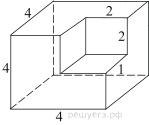
7. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

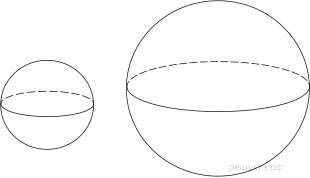
8. Во сколько раз увеличится объем шара, если его радиус увеличить в три раза?

9. Радиусы двух шаров равны 32 и 60. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.

10. Объем конуса равен 10. Через середину высоты параллельно основанию конуса проведено сечение, которое является основанием меньшего конуса с той же вершиной. Найдите объем меньшего конуса.

Вариант 2 8. Стереометрия

1. Диаметр основания конуса равен 42, а длина образующей равна 75. Найдите высоту конуса.

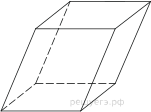
2. Гранью параллелепипеда является ромб со стороной 4 и острым углом 30°. Одно из ребер параллелепипеда составляет с этой гранью угол в 30° и равно 6. Найдите объем параллелепипеда.

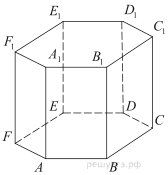
3. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁, C₁, D₁ правильной шестиугольной призмы ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 9, а боковое ребро равно 10.

4. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 4 и 16. Найдите ребро равновеликого ему куба.

5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

6. В правильной четырехугольной пирамиде точка — центр основания, вершина, , Найдите длину отрезка

7. Гранью параллелепипеда является ромб со стороной 1 и острым углом 45°. Одно из ребер параллелепипеда составляет с этой гранью угол в 45° и равно 5. Найдите объем параллелепипеда.

8. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

9. Конус вписан в шар. Радиус основания конуса равен радиусу шара. Объём шара равен 112. Найдите объём конуса.

10.Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.

Вариант 3 8. Стереометрия

1. На рисунке изображён многогранник, все двугранные углы многогранника прямые. Найдите тангенс угла C₂C₃B₂.

2. Найдите угол CAD₂ многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

3. Найдите угол многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

4. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объем параллелепипеда.

5. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

6. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 0,5 и 16. Найдите ребро равновеликого ему куба.

7. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 24. Найдите объем пирамиды.

8. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 6. Найдите объем пирамиды.

9. Объем правильной четырехугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

10. В прямоугольном параллелепипеде известно, что Найдите длину ребра

Вариант 4 8. Стереометрия

1. Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

2. В прямоугольном параллелепипеде известно, что Найдите длину ребра

3. Площадь боковой поверхности цилиндра равна 18, а диаметр основания равен 9. Найдите высоту цилиндра.

4. Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в три раза?

5. Найдите объём многогранника, вершинами которого являются точки правильной треугольной призмы площадь основания которой равна 9, а боковое ребро равно 8.

6. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 2 и 3. Объем призмы равен 18. Найдите ее боковое ребро.

7. Найдите объем многогранника, вершинами которого являются точки , , , , , , правильной шестиугольной призмы , площадь основания которой равна 4, а боковое ребро равно 3.

8. Конус описан около правильной четырехугольной пирамиды со стороной основания 3 и высотой 13. Найдите его объем, деленный на π.

9. Диагональ куба равна 13. Найдите площадь его поверхности.

10. Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 48 и высота равна 7.

Вариант 5 8. Стереометрия

1. Диагональ куба равна 1. Найдите площадь его поверхности.

2. Найдите объем пирамиды, высота которой равна 6, а основание – прямоугольник со сторонами 3 и 4.

3. В правильной треугольной призме ABCA₁B₁C₁ стороны оснований равны 2, боковые рёбра равны 5. Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер AB, AC, A₁B₁ и A₁C₁.

4. Найдите квадрат расстояния между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

5. В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в раза больше первого? Ответ выразите в см.

6. В сосуд, имеющий форму правильной треугольной призмы, налили 2300 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см³.

7. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.

8. В основании прямой призмы лежит прямоугольный треугольник с катетами 6 и 8. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

9. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы

10.Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 25. Найдите объём цилиндра.

Вариант 6 8. Стереометрия

1. В правильной треугольной пирамиде SABC точка K – середина ребра BC, S – вершина. Известно, что SK = 4, а площадь боковой поверхности пирамиды равна 54. Найдите длину ребра AC.

2. Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

3. Во сколько раз увеличится объем куба, если его ребра увеличить в пятнадцать раз?

4. Найдите объем многогранника, вершинами которого являются точки , , , , , , , правильной шестиугольной призмы , площадь основания которой равна 6, а боковое ребро равно 2.

5. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁, C₁, D₁ правильной шестиугольной призмыABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 6, а боковое ребро равно 2.

6. Гранью параллелепипеда является ромб со стороной 1 и острым углом 60°. Одно из ребер параллелепипеда составляет с этой гранью угол в 60° и равно 2. Найдите объем параллелепипеда.

7. Цилиндр описан около шара. Объем цилиндра равен 33. Найдите объем шара.

8. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

9. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

10. Цилиндр описан около шара. Объем шара равен 24. Найдите объем цилиндра.

Вариант 7 8. Стереометрия

1. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

2. Найдите объем части конуса, изображенной на рисунке. В ответе укажите

3. В основании прямой призмы лежит квадрат со стороной 2. Боковые ребра равны Найдите объем цилиндра, описанного около этой призмы.

4. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

5. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

6. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

7. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

8. Найдите объем части цилиндра, изображенной на рисунке. В ответе укажите

9. Найдите объем части конуса, изображенной на рисунке. В ответе укажите

10. Найдите объем части конуса, изображенной на рисунке. В ответе укажите

Вариант 8 8. Стереометрия

1. Объем одного куба в 729 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

2. В правильной четырехугольной пирамиде точка — центр основания, вершина, , Найдите длину отрезка

3. В правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.

4. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.

5. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.

6. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.

7. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.

8. В правильной треугольной пирамиде медианы основания пересекаются в точке Объем пирамиды равен , Найдите площадь треугольника

9. В прямоугольном параллелепипеде известно, что , , Найдите длину ребра

10. Высота конуса равна 4, а диаметр основания — 6. Найдите образующую конуса.

Вариант 9 8. Стереометрия

1. Найдите расстояние между вершинами и многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

2. Найдите площадь поверхности пространственного креста, изображенного на рисунке и составленного из единичных кубов.

3. Высота конуса равна 6, образующая равна 10. Найдите площадь его полной поверхности, деленную на

4. Площадь боковой поверхности конуса в два раза больше площади основания. Найдите угол между образующей конуса и плоскостью основания. Ответ дайте в градусах.

5. Площадь полной поверхности конуса равна 12. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 1:1, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.

6. Объем одного шара в 27 раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

7. Радиусы двух шаров равны 6 и 8. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.

8. Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

9. Объем куба равен 12. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

10. В правильной четырёхугольной пирамиде высота равна 2, боковое ребро равно 5. Найдите её объём.

Вариант 10 8. Стереометрия

1. Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A₁, B₁, C₁, D₁ правильной шестиугольной призмыABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 6, а боковое ребро равно 2.

2.Высота конуса равна 12, образующая равна 15. Найдите его объем, деленный на

3. В правильной четырехугольной пирамиде SABCD точка O — центр основания, S вершина, SO = 4, AC = 6. Найдите боковое ребро SC.

4. В правильной четырехугольной пирамиде точка О — центр основания, вершина, , Найдите длину отрезка

5. В правильной четырехугольной пирамиде точка — центр основания, вершина, , Найдите длину отрезка

6. ЗВ правильной треугольной пирамиде SABC точка R — середина ребра BC, S — вершина. Известно, что AB = 1, а SR = 2. Найдите площадь боковой поверхности.

7. В правильной треугольной пирамиде SABC точка N — середина ребра BC, S — вершина. Известно, что AB = 1, а площадь боковой поверхности равна 3. Найдите длину отрезка SN.

8. В правильной треугольной пирамиде SABC точка L — середина ребра BC, S — вершина. Известно, что SL = 2, а площадь боковой поверхности равна 3. Найдите длину отрезка AB.

9. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, объем пирамиды равен 1. Найдите длину отрезка MS.

10. В правильной треугольной пирамиде SABC медианы основания пересекаются в точке M. Площадь треугольника ABC равна 3, MS = 1. Найдите объем пирамиды.

8. Стереометрия

Вариант 1

12
166,5
60
2
28
75
96
27
68
1,25

Вариант 2

Вариант 3

3
60
45
4
152
2
2304
48
29
4

Вариант 4

29
5
2
27
24
6
4
19,5
338
4704

Вариант 5

Вариант 6

9
45
3375
8
6
1,5
22
110
94
36

Вариант 7

340
216
4
3,75
144
937,5
14
105
87,75
243

Вариант 8

Вариант 9

Вариант 10

Источник

Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

В основании правильной треугольной призмы ABCA₁B₁C₁ лежит треугольник со стороной 6. Высота призмы равна 4. Точка N  — середина ребра A₁C₁.

а)  Постройте сечение призмы плоскостью BAN.

б)  Найдите периметр этого сечения.

В правильной четырехугольной пирамиде PABCD, все ребра которой равны 4, точка K ― середина бокового ребра AP.

а)  Постройте сечение пирамиды плоскостью, проходящей через точку K и параллельной прямым PB и BC.

б)  Найдите площадь сечения.

Источник: Пробный экзамен Санкт-Петербург 2015. Вариант 1.

На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E : EA = 5 : 3, на ребре BB₁  — точка F так, что B₁F : FB = 5 : 11, а точка T − середина ребра B₁C₁. Известно, что AD = 10, AA₁  =  16.

а)  Докажите, что плоскость EFT проходит через вершину D₁.

б)  Найдите площадь сечения параллелепипеда плоскостью EFT.

На ребре AA₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ взята точка E так, что A₁E  =  6EA. Точка T  — середина ребра B₁C₁. Известно, что AD  =  12, AA₁  =  14.

а)  Докажите, что плоскость ETD₁ делит ребро BB₁ в отношении 4 : 3.

б)  Найдите площадь сечения параллелепипеда плоскостью ETD₁.

Основанием прямой четырехугольной призмы ABCDA’B’C’D’ является квадрат ABCD со стороной высота призмы равна Точка K  — середина ребра BB’. Через точки K и С’ проведена плоскость α, параллельная прямой BD’.

а)  Докажите, что сечение призмы плоскостью α является равнобедренным треугольником.

б)  Найдите периметр треугольника, являющегося сечением призмы плоскостью α.

Источник: ЕГЭ по математике 2015. Досрочная волна, резервная волна (часть С)

Пройти тестирование по этим заданиям

Источник

8. Геометрия в пространстве (стереометрия)

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Задачи по стереометрии (геометрии в пространстве)

Задание
1

#934

Уровень задания: Равен ЕГЭ

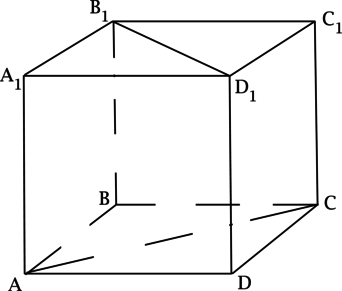
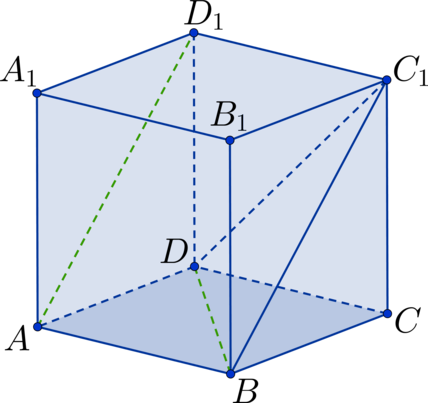
(ABCDA_1B_1C_1D_1) – куб. Найдите угол между прямыми, содержащими отрезки (AC) и (B_1D_1). Ответ дайте в градусах.

Прямая (BD) параллельна прямой (B_1D_1), тогда угол между (AC) и (B_1D_1) равен углу между (AC) и (BD), но (AC) и (BD) – диагонали квадрата, тогда они пересекаются под прямым углом, следовательно ответ (90^{circ}).

Ответ: 90

Задание
2

#2847

Уровень задания: Равен ЕГЭ

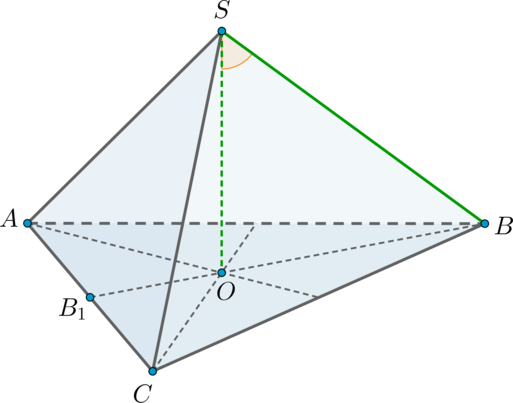
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите угол между высотой пирамиды и ребром (SB), если высота пирамиды равна (2sqrt3), а сторона основания пирамиды равна (6). Ответ дайте в градусах.

Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, высота (SO) падает в точку пересечения медиан основания.

Пусть (BB_1) – медиана, а значит, и высота. По теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=3sqrt3 quadRightarrowquad BO=dfrac23BB_1=2sqrt3,] так как медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Следовательно, прямоугольный (triangle SOB) является равнобедренным ((SO=BO=2sqrt3)), значит, острые углы равны по (45^circ).

Ответ: 45

Задание
3

#933

Уровень задания: Равен ЕГЭ

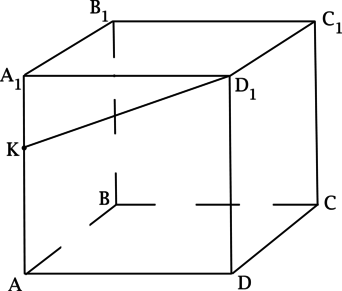
(ABCDA_1B_1C_1D_1) – куб. Точка (K) лежит на ребре (AA_1). Найдите угол между прямыми, содержащими отрезки (D_1K) и (AB). Ответ дайте в градусах.

Так как (ABCDA_1B_1C_1D_1) – куб, то (AB) перпендикулярен плоскости ((ADD_1)), тогда (AB) перпендикулярен любой прямой, лежащей в плоскости ((ADD_1)), следовательно, угол между прямыми, содержащими отрезки (D_1K) и (AB) равен (90^{circ}).

Ответ: 90

Задание
4

#2845

Уровень задания: Равен ЕГЭ

Дан правильный тетраэдр (SABC). Найдите квадрат тангенса угла между высотой грани (SAC), опущенной из вершины (S), и высотой грани (ABC), опущенной из вершины (B).

Пусть (SB_1) – высота грани (SAC). Так как тетраэдр правильный, то все его грани – равные правильные треугольники, то есть (SB_1) также является и медианой, значит, (AB_1=B_1C). Также у правильного тетраэдра высота из каждой вершины падает в точку пересечения медиан (биссектрис, высот) противоположной грани. Следовательно, если (SO) – высота, то (O) – точка пересечения медиан треугольника (ABC), а значит и высот, так как (triangle ABC) правильный. Следовательно, (BB_1) — медиана и высота.

Таким образом, необходимо найти (mathrm{tg}^2angle (SB_1,
BB_1)).
Пусть (a) – ребро тетраэдра. Тогда (BC=a, B_1C=0,5a), следовательно, по теореме Пифагора [BB_1=sqrt{BC^2-B_1C^2}=dfrac{sqrt3}2a] Так как (O) – точка пересечения медиан, а медианы точкой пересечения делятся в отношении (2:1), считая от вершины, то (OB_1=frac13BB_1=frac{sqrt3}6a).

Так как (triangle ABC=triangle SAC), то (SB_1=BB_1). Следовательно, из прямоугольного (triangle SB_1O): [cos
alpha=dfrac{OB_1}{SB_1}=dfrac13 quadRightarrowquad sin alpha
=sqrt{1-cos^2alpha}=dfrac{2sqrt2}3 quadRightarrowquad
mathrm{tg}^2alpha=(2sqrt2)^2=8.]

Ответ: 8

Задание
5

#1846

Уровень задания: Равен ЕГЭ

Дан куб (ABCDA_1B_1C_1D_1). Найдите угол между прямыми (AD_1) и (BD). Ответ дайте в градусах.

Заметим, что (BC_1 || AD_1), тогда рассмотрим треугольник (triangle BDC_1), в котором необходимо определить (angle DBC_1). Он состоит из диагоналей соответствующих квадратов. Так как квадраты между собой равны, то равны и диагонали (Rightarrow) (triangle BDC_1) – равносторонний треугольник (Rightarrow) (angle DBC_1 = 60^circ).

Ответ: 60

Задание
6

#1847

Уровень задания: Равен ЕГЭ

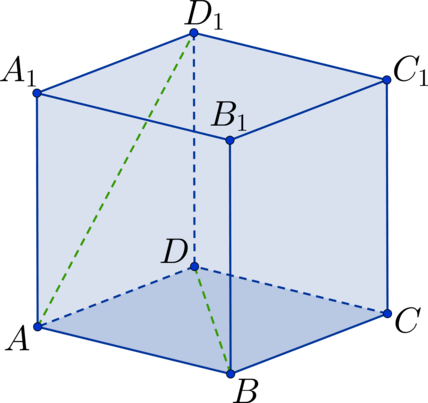
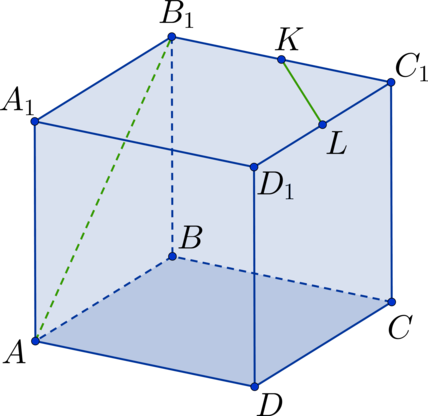
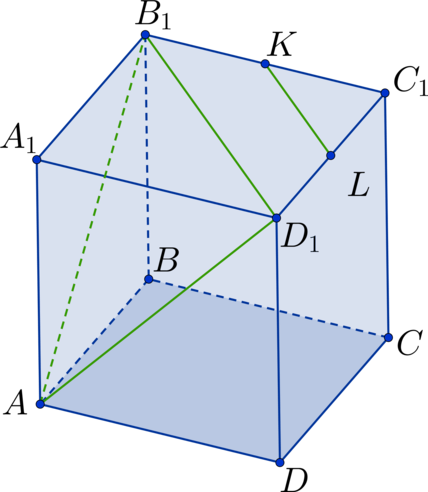
Дан куб (ABCDA_1B_1C_1D_1). Точка (K) – середина стороны (B_1C_1), а точка (L) – середина стороны (C_1D_1). Найдите угол между прямыми (AB_1) и (KL). Ответ дайте в градусах.

Проведем диагональ (B_1D_1) в квадрате (A_1B_1C_1D_1). Тогда (KL) – средняя линия в (triangle B_1C_1D_1) (Rightarrow) (KL || B_1D_1) (Rightarrow) (angle AB_1D_1) – искомый угол. Рассмотрим (triangle AB_1D_1). Он состоит из диагоналей соответствующих квадратов (Rightarrow) треугольник является равносторонним (Rightarrow) (angle AB_1D_1 = 60^circ).

Ответ: 60

Задание
7

#2846

Уровень задания: Сложнее ЕГЭ

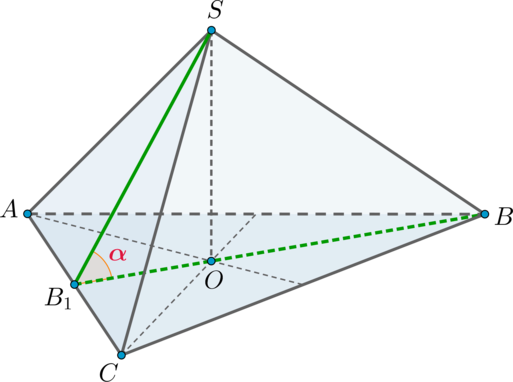
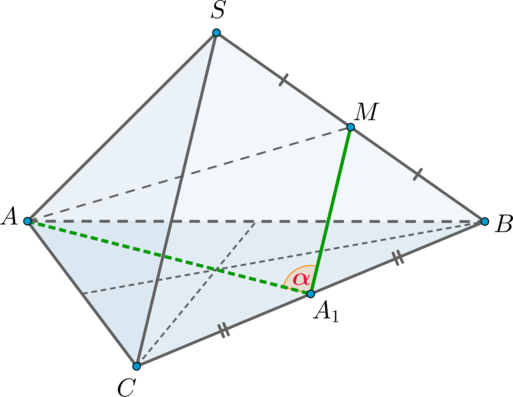
Дана правильная треугольная пирамида (SABC) с вершиной (S). Найдите косинус угла между высотой основания (AA_1) и ребром (SC), если сторона основания равна (sqrt3), а боковое ребро равно (2).

Так как пирамида правильная, то в основании лежит правильный треугольник, следовательно, (AA_1) также является и медианой.

Заметим, что прямые (AA_1) и (SC) скрещиваются. Проведем (A_1Mparallel SC), следовательно, (angle (AA_1, SC)=angle (AA_1,
A_1M)).
Так как (A_1Mparallel SC) и (A_1) – середина (BC), то (M) – середина (SB). Следовательно, (A_1M) – средняя линия и [A_1M=frac12SC=1.] По теореме Пифагора из (triangle ABA_1): [AA_1=sqrt{AB^2-A_1B^2}=dfrac32.] Медиану (AM) из (triangle SAB) можно найти по формуле медианы: [AM^2=dfrac{2AS^2+2AB^2-SB^2}4=dfrac52.] Следовательно, по теореме косинусов из (triangle AA_1M): [cos alpha=dfrac{AA_1^2+A_1M^2-AM^2}{2AA_1cdot A_1M}=dfrac14=0,25.]

Ответ: 0,25

Старшеклассникам, планирующим хорошо сдать ЕГЭ по математике, мы рекомендуем повторить стереометрию. Это раздел геометрии, в котором изучаются свойства фигур (точек, прямых, плоскостей и т. д.) в пространстве. Используя нашу базу тренировочных задач, вы сможете устранить пробелы в знаниях по стереометрии, при этом подготовка к экзамену не потребует материальных вложений. Вы разберетесь в теме без репетитора, так как мы изложили материал в максимально доступной форме.

В данном учебном пособии рассмотрены стандартные математические задания по теме «Геометрия фигур в пространстве», предлагавшиеся на ЕГЭ в прошлых учебных годах. Здесь вы сможете вспомнить теоретическую базу и применить свои знания на практике. У нас вы найдете как элементарные упражнения, так и материалы повышенной сложности, также изучаемые в школьной программе. При этом каждая задача по стереометрии содержит подробный алгоритм решения и правильный ответ.

Тренируйтесь регулярно, и вы не совершите ошибок на аттестационном экзамене, например, если вам достанутся задачи на тему «Вычисление объемов фигур». А благодаря порталу «Школково» заниматься самообразованием можно в любое удобное время онлайн. Приступите к решению задач из раздела ЕГЭ «Геометрия в пространстве» уже сейчас, ведь с каждым днем остается все меньше времени на подготовку. А мы всегда рады помочь.

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

Инфоурок

›

Геометрия

›Презентации›Тренажёр «Решу ЕГЭ: стереометрия, цилиндр»(профиль)

Тренажёр «Решу ЕГЭ: стереометрия, цилиндр»(профиль)

Скачать материал

Сейчас обучается 82 человека из 34 регионов

Сейчас обучается 38 человек из 28 регионов

Сейчас обучается 43 человека из 27 регионов

Описание презентации по отдельным слайдам:

1 слайд

Решу ЕГЭ: стереометрия, цилиндр(профиль)
ТП«Анимированная сорбонка с удалением»
Автор: Иванова Нина Николаевна,
учитель математики
МОУ «СОШ» с. Большелуг
Корткеросский район
Республика Коми
2 слайд

Реши задачу и напиши ответ
В цилиндрический сосуд налили 2000 см3 воды. Уровень воды при этом достигает высоты 12 см. В жидкость полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 9 см. Чему равен объем детали? Ответ выразите в см3.
Объём детали равен объёму вытесненной ею жидкости. Объём вытесненной жидкости равен 9/12 исходного объёма Vдет=9:122000=1500см3
1
3 слайд

В цилиндрическом сосуде уровень жидкости достигает 16 см. На какой высоте будет находиться уровень жидкости, если ее перелить во второй сосуд, диаметр которого в 2 раза больше первого? Ответ выразите в см.
Объем цилиндрического сосуда выражается через его диаметр и высоту как V=Hπd2:4. При увеличении диаметра сосуда в 2 раза высота равного объема жидкости уменьшится в 4 раза и станет равна 4.
2
Реши задачу и напиши ответ
4 слайд

Реши задачу и напиши ответ
Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π
Площадь боковой поверхности цилиндра S=2πrH, поэтому
S=2π 23=12π Ответ: 12
3
5 слайд

В цилиндрический сосуд налили 6 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,5 раза. Найдите объём детали. Ответ выразите в куб. см.
Объем детали равен объему вытесненной ею жидкости. Объем вытесненной жидкости равен 1/2 исходного объема, поэтому объем детали равен 3 куб. см.
4
Реши задачу и напиши ответ
6 слайд

Реши задачу и напиши ответ
Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.
Площадь боковой поверхности цилиндра равна S=2πrh=Ch,где C – длина окружности основания. Поэтому S=32=6
5
7 слайд

Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
Площадь боковой поверхности цилиндра равна произведению длины окружности, лежащей в основании, на высоту. Поэтому высота цилиндра равна 2.
6
Реши задачу и напиши ответ
8 слайд

Реши задачу и напиши ответ
Площадь боковой поверхности цилиндра равна 12π, а диаметр основания — 1. Найдите высоту цилиндра.
Площадь боковой поверхности цилиндра находится по формуле:S=2πrh, значит
h=S : 2πrh=2
7
9 слайд

Источники:
https://www.proza.ru/pics/2018/01/02/1273.jpg
https://pbs.twimg.com/profile_images/803298673274880000/DVNYOQeM.jpg
http://raivatala2008.narod.ru/images/GIA.jpg
https://www.tyuiu.ru/wp-content/uploads/2016/02/1391685511_011-1024×734.jpg
https://biblionika.info/uploads/posts/2018-09/1536611724_456.png
https://images.theabcdn.com/i/29175531

Шаблон авторский
Автора технологического приема Г.О.Аствацатурова http://didaktor.ru/kak-sdelat-sorbonku-bolee-interaktivnoj
МК №2 Создание анимированной сорбонки с удалением
« Решу ЕГЭ»: математика. ЕГЭ-2019:задания,ответы, решения. Обучающая система Дмитрия Гущина https://math-ege.sdamgia.ru/test?theme=194

Краткое описание документа:

Тренажёр «Решу ЕГЭ: стереометрия, цилиндр»(профиль) предназначен в помощь учителям по организации заинтересованности повторения к занятиям по данной теме при подготовке к итоговой аттестации. Работу можно применить при проведении урока по математике, систематизации, закреплении и проверке знаний учащихся. В презентации использован технологический прием Г.О.Аствацатурова «Анимированные сорбонки с удалением». Для того, чтобы получить решение, надо нажать на сорбонку. Рассмотрены 7 задач с их решения.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 156 856 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Курс повышения квалификации «Подростковый возраст — важнейшая фаза становления личности»
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс профессиональной переподготовки «Экскурсоведение: основы организации экскурсионной деятельности»
Курс повышения квалификации «Основы построения коммуникаций в организации»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»
Курс профессиональной переподготовки «Организация деятельности по водоотведению и очистке сточных вод»
Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»
Курс профессиональной переподготовки «Информационная поддержка бизнес-процессов в организации»

Настоящий материал опубликован пользователем Иванова Нина Николаевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.

Удалить материал
- На сайте: 5 лет
- Подписчики: 3
- Всего просмотров: 399492
- Всего материалов:
  
  356

Источник

1.	Как на ЕГЭ (1). Задача по стереометрии (с ручной проверкой)	3 Б.
2.	Объём пирамиды с прямоугольным основанием (с ручной проверкой)	3 Б.

Вход

или
Регистрация

Источник

По теме: методические разработки, презентации и конспекты

Решение стереометрической задачи тремя различными способами

Методическая разработка по теме: «Применение аналитической геометрии к решению стереометрических задач».

Тема 36. ГЕОМЕТРИЯ.ОСНОВНЫЕ СВЕДЕНИЯ ДЛЯ РЕШЕНИЯ СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ.

Тема 37.ИТОГОВЫЙ КОНТРОЛЬ ПО ТЕМАМ 34-36: «РЕШЕНИЕ ПЛАНИМЕТРИЧЕСКИХ И СТЕРЕОМЕТРИЧЕСКИХ ЗАДАЧ»

Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»

Методическая разработка по теме: «Применение векторно-координатного метода в решении стереометрических задач»

Тренажёр по геометрии. Стереометрия в задачах ЕГЭ.

Задачи по стереометрии (геометрии в пространстве)

Тренажёр «Решу ЕГЭ: стереометрия, цилиндр»(профиль)

Описание презентации по отдельным слайдам:

Краткое описание документа:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Новое и интересное на сайте: