3 студента сдают экзамен. Вероятность успешной сдачи для 1-го 0,9, для второго — 0,7, для третьего — 0,9. Найти вероятность того что:
а) все трое сдали экзамен;
б) двое сдали экзамен;
в) хотя бы один студент сдал экзамен.
вероятности
теория
задан
13 Апр ’15 21:26
мандаринка
1●2●8
20% принятых
изменен
14 Апр ’15 8:56
Виталина
99●1●7
а) Перемножьте три вероятности.
б) $%0,9cdot0,7(1-0,9)+0,9(1-0,7)0,9+(1-0,9)0,7cdot0,9$%.
в) $%1-(1-0,9)(1-0,7)(1-0,9)$%.
(14 Апр ’15 0:07)
falcao
10|600
символов нужно
символов осталось
Найди верный ответ на вопрос ✅ «Три студента сдают экзамен. Вероятность успешной сдачи экзамена для первого студента равняется 0.9, для второго 0.8, для третьего 0.5. …» по предмету 📙 Алгебра, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Искать другие ответы
Главная » ⭐️ Алгебра » Три студента сдают экзамен. Вероятность успешной сдачи экзамена для первого студента равняется 0.9, для второго 0.8, для третьего 0.5. Какая вероятность того что экзамен сдадут: а) все три студента б) только один студент
Сессия состоит из трех экзаменов. Вероятность того, что студент сдаст первый экзамен, равна 0,9, вероятность сдачи второго — 0,9, а третьего – 0,7. Найти вероятности событий:
А – студент сдаст все три экзамена;
В – студент сдаст не менее двух экзаменов.
Решение:
Пусть событие D – студент сдает первый экзамен, событие Е — сдаст второй экзамен, событие С – сдаст третий, событие F – сдаст два экзамена.
1) Событие А – студент сдаст все три экзамена;
Р(А)= Р(D)•Р(Е)•Р(С) = 0,9•0,9•0,7= 0,567
2) В – студент сдаст не менее двух экзаменов.
Событие F = D•Е• 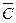
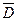

Найдем вероятность сдачи только двух экзаменов
Р(F)=Р(DЕ 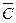
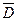

Тогда вероятность сдать не менее двух экзаменов найдем по формуле Р(В)=Р(А) + Р(F)= 0,567+0,369=0,936
Ответ: 1) 0,567; 2) 0,936.
|
Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где… |
Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса… |
Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар… |
Расчетные и графические задания Равновесный объем — это объем, определяемый равенством спроса и предложения… |
ЗАДАЧА 1 3
ЗАДАЧА 2. 3
ЗАДАЧА 3. 4
ЗАДАЧА 45
Список используемой литературы 7
Задания к работе:
ЗАДАЧА 1
Три студента сдают экзамен. Вероятность того, что первый сдаст на «отлично» равна 0,7, второй сдаст на «отлично» – 0,6, третий – 0,2. Какова вероятность того, что экзамен будет сдан на «отлично»: а) только одним студентом, б) на «отлично» не сдаст ни один студент?..
…
ЗАДАЧА 4.
Функция распределения непрерывной случайной величины задана сле-дующим образом:
Найти: 1) a, b;
2) f(x) – плотность распределения;
3) M[x], D[x],
4) P(2 ≤ x ≤ 3);
5) построить графики функций F(x) и f(x)…
1. П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. Высшая математика в упражнениях и задачах. Часть 2. Москва ОНИКС 21 век. Мир и образование. 2004г.
2. В. Е. Гмурман. Теория вероятностей и математическая статистика. М.: Высшая школа. 2003г.-450с.
3. В. Е. Гмурман. Руководство к решению задач по теории вероятностей и математической статистике. М.: Высшая школа. 2002г.
| Тема: | Вариант 26 Задача 1 Три студента сдают экзамен. Вероятность того, что первый сдаст на «отлично» равна 0,7, второй сдаст на «отлично» – 0,6, третий – 0,2. Какова вероятность того, что экзамен будет сдан на «отлично»: а) только одним студентом, б) на «отлично» не сдаст ни один студент?.. Задача 4. Функция распределения непрерывной случайной величины задана сле-дующим образом: Найти: 1) a, b; 2) f(x) – плотность распределения; 3) M[x], D[x], 4) P(2 ≤ x ≤ 3); 5) построить графики функций F(x) и f(x)… |
| Артикул: | 1800704 |
| Дата написания: | 10.08.2008 |
| Тип работы: | Контрольная работа |
| Предмет: | Теория вероятностей |
| Оригинальность: | Антиплагиат.ВУЗ — 80% |
| Количество страниц: | 7 |
OBRAZOVALKA.COM
OBRAZOVALKA.COM — образовательный портал
Наш сайт это площадка для образовательных консультаций, вопросов и ответов для школьников и студентов .
На вопросы могут отвечать также любые пользователи, в том числе и педагоги.
Консультацию по вопросам и домашним заданиям может получить любой школьник или студент.
1) Три студента сдают экзамены. Возможность того, что 1-ый сдаст на отлично — 0,7 , 2-ой сдаст на отлично — 0,6 , а 3-ий — 0,2. Какова вероятность, что экзамен будет сдан на отлично только одним студентом. На отлично не сдаст ни один студент?
2)В первом ящике 20 деталей, из их 4 бракованных. Во втором ящике 30 деталей — 5 бракованных.из первого ящика во второй переложили 2 детали, отыскать вероятность того, что деталь извлеченная из второго ящика после этого , окажется бракованной?
Задать свой вопрос
1 ответ
2019-04-26 12:06:24
Поглядите решение первой задачки:
если принять, что р — студент сдал на «отлично» (это 0,7; 0,6 и 0,2), а q=1-р — не сдал на «отлично», то по формуле полной вероятности
для случая, что один студент сдаст на «отлично»:
Р=pqq+qpq+qqp=0.7*0.4*0.8+0.3*0.6*0.8+0.3*0.4*0.2=0.392
а для варианта, когда ни один на «отлично» не сдаст:
P=qqq=0.3*0.4*0.8=0.096
-
Вопросы ответы
Добро пожаловать!
Для того чтобы стать полноценным пользователем нашего портала, вам необходимо пройти регистрацию.
Авторизоваться
Уже зарегистрированны? А ну-ка живо авторизуйтесь!
Войти на сайт
|
забыли пароль? Помощь сайту |
Вопросы »Комбинаторика,вероятность » теория вероятности теория вероятности создана: 01.12.2013 в 08:08
kate_93 : Здравствуйте.Помогите пожалуйста решить эту задачу. В ящике 9 красных и 5 синих кубика. Из ящика наудачу вынимают три кубика. Какова вероятность, что два кубика синих, один красный?
Хочу написать ответ |







