Тригонометрические функции егэ задание 9 - Exhelper.top

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №9. Тригонометрические функции

ЕГЭ Профиль №9. Тригонометрические функцииadmin2022-08-22T20:57:39+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №9. Тригонометрические функции

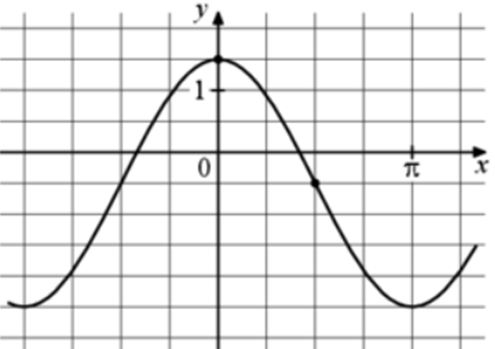
Задача 1. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a. Ответ ОТВЕТ: 2.
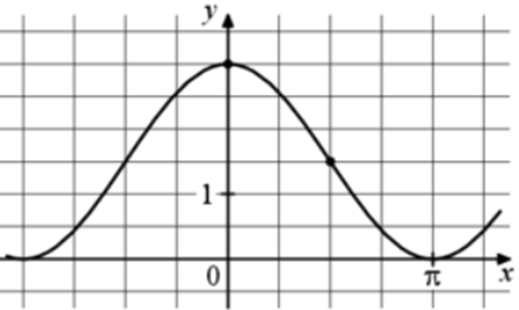
Задача 2. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a. Ответ ОТВЕТ: 1,5.
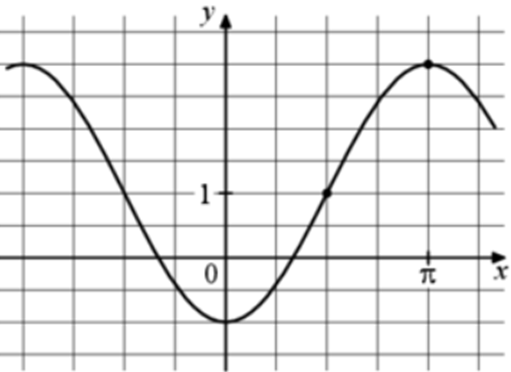
Задача 3. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a. Ответ ОТВЕТ: — 2.
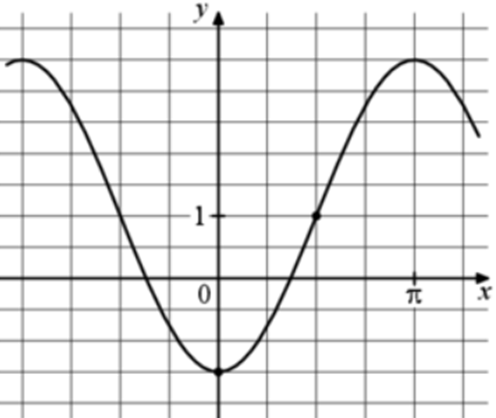
Задача 4. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите a. Ответ ОТВЕТ: — 2,5.
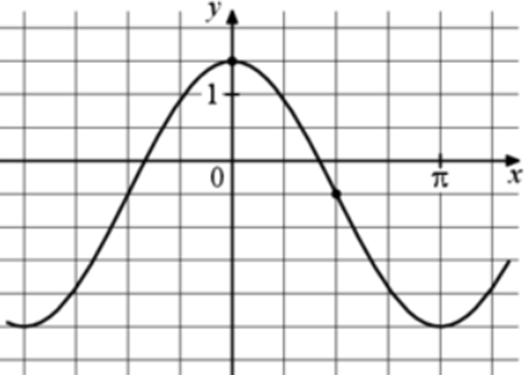
Задача 5. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b. Ответ ОТВЕТ: — 0,5.
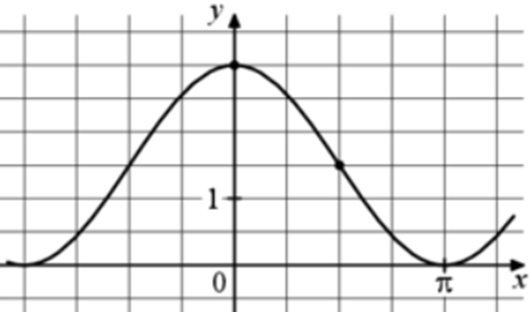
Задача 6. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b. Ответ ОТВЕТ: 1,5.
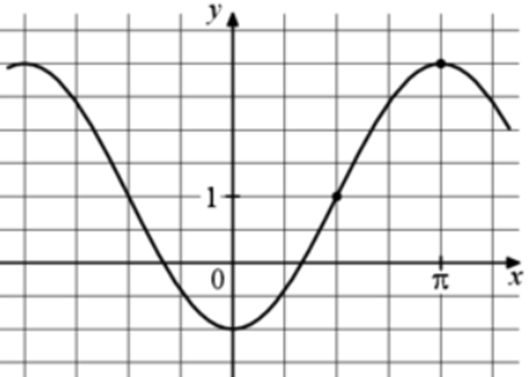
Задача 7. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b. Ответ ОТВЕТ: 1.
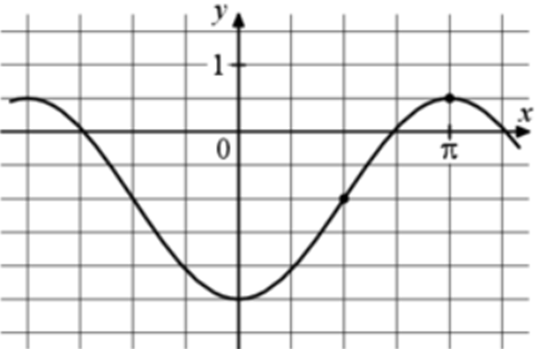
Задача 8. На рисунке изображён график функции (fleft( x right) = a,,cos x + b.) Найдите b. Ответ ОТВЕТ: — 1.
Задача 9. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a. Ответ ОТВЕТ: 2,5.
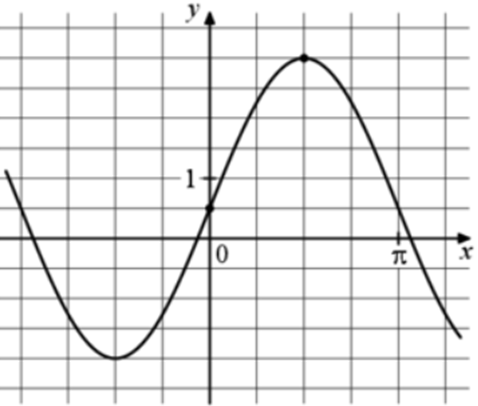Задача 10. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a. Ответ ОТВЕТ: 0,5.
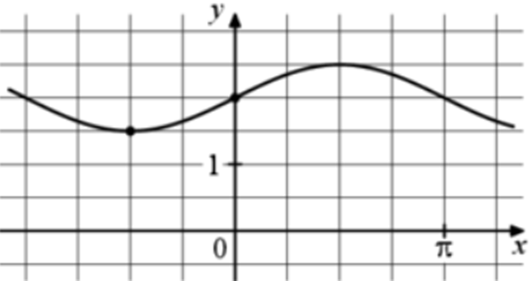Задача 11. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a. Ответ ОТВЕТ: — 1,5.
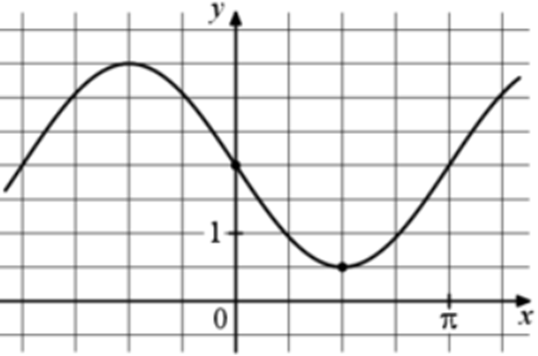Задача 12. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите a. Ответ ОТВЕТ: — 2,5.

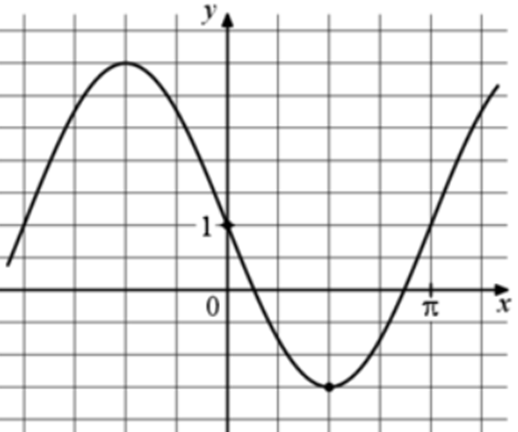Задача 13. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ ОТВЕТ: 0,5.
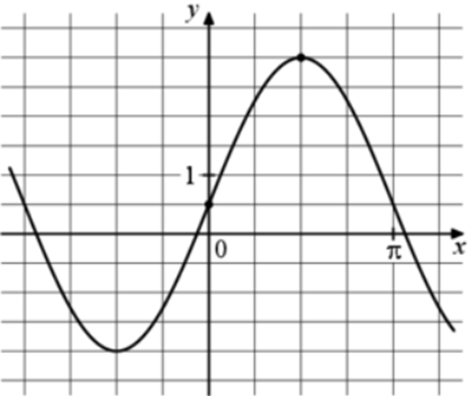Задача 14. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ ОТВЕТ: — 0,5.
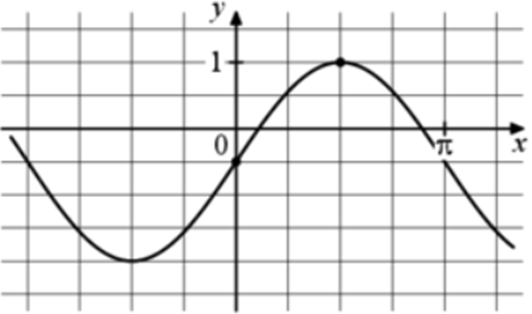Задача 15. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ ОТВЕТ: 0,5.
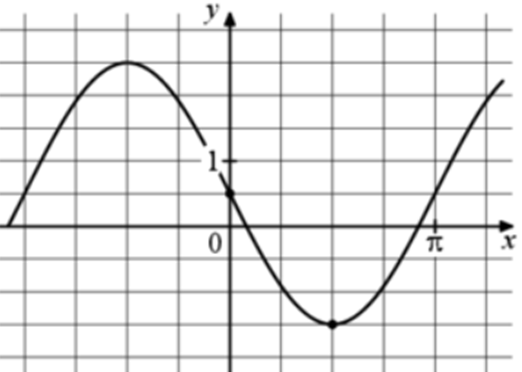Задача 16. На рисунке изображён график функции (fleft( x right) = a,,sin x + b.) Найдите b. Ответ ОТВЕТ: — 0,5.
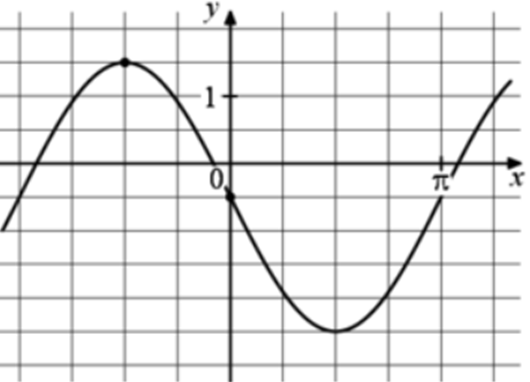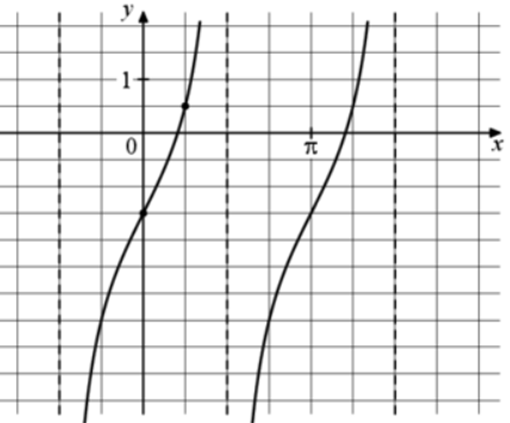
Задача 17. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a. Ответ ОТВЕТ: 2.
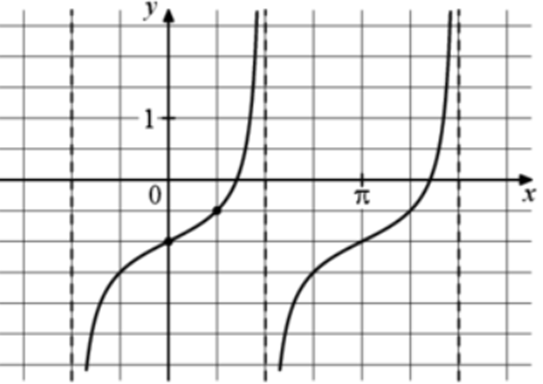
Задача 18. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a. Ответ ОТВЕТ: 0,5.
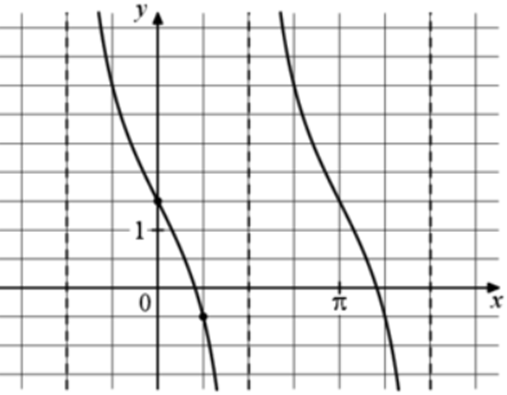
Задача 19. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a. Ответ ОТВЕТ: — 2.
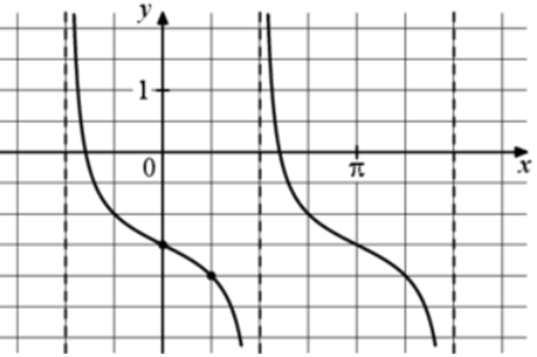
Задача 20. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите a. Ответ ОТВЕТ: — 0,5.
Задача 21. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b. Ответ ОТВЕТ: 1.
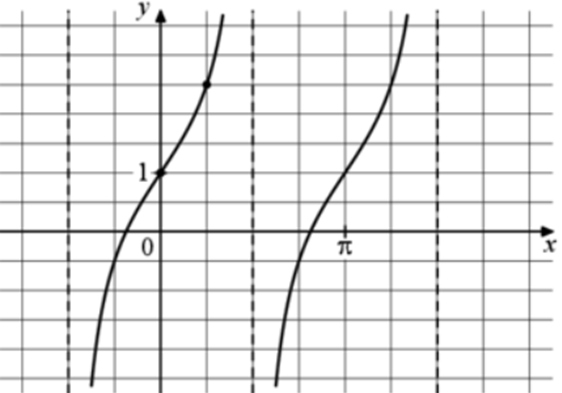Задача 22. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b. Ответ ОТВЕТ: — 1.
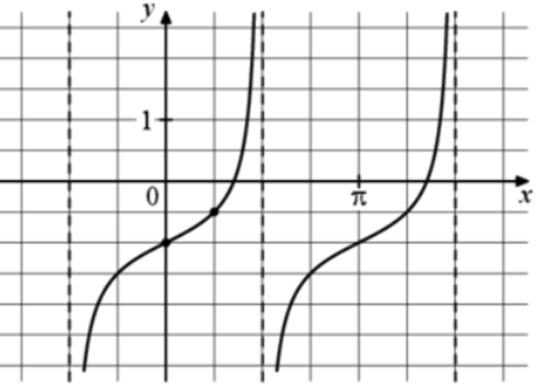Задача 23. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b. Ответ ОТВЕТ: 1,5.
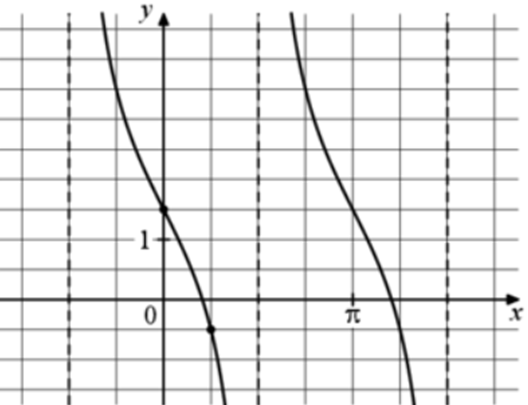Задача 24. На рисунке изображён график функции (fleft( x right) = a,,{text{tg}},x + b.) Найдите b. Ответ ОТВЕТ: — 1,5.

Источник

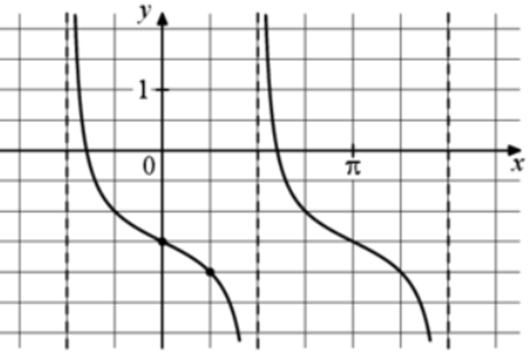Скачать материал

Сейчас обучается 23 человека из 17 регионов

Сейчас обучается 99 человек из 37 регионов

Курс добавлен 16.12.2022
Сейчас обучается 20 человек из 14 регионов

Описание презентации по отдельным слайдам:

1 слайд

Преобразование графиков тригонометрических функций
Задание 9. ЕГЭ 2022
2 слайд

y = f(x) + b
Параллельный перенос вдоль оси ординат
3
-3
𝑦=sin𝑥 + 1
𝑦=sin𝑥 — 1
3 слайд

y = f(x + a)
Параллельный перенос вдоль оси абсцисс
𝑦=cos(𝑥+ 𝜋 4 )
𝑦=cos(𝑥− 𝜋 4 )
4 слайд

y = mf(x), где m>1
Растяжение от оси х с коэффициентом m
3
-3
𝑦=3sin𝑥
5 слайд

y = mf(x), где 0<m<1
Сжатие к оси х с коэффициентом 1 m
𝑦=0,5cos𝑥
6 слайд

y = mf(x), где m=-1
Преобразование симметрии относительно оси х
𝑦=−cos𝑥
7 слайд

1. Задание 9 № 564531
На рисунке изображён график функции вида
где числа a, b, c, d — целые числа . Найдите
8 слайд

Растянули в 2 раза, следовательно a=2
Не сдвигали вдоль оси ОХ, следовательно с=0
Сдвинули вдоль оси ОУ, вниз на 1 единицу, d=-1
9 слайд

Мы получили, что а=2; с=0; d=-1
Найдём период функции:

Получили, что период =, а по графику период равен 2, следовательно
Искомая функция принимает вид:
10 слайд

2. Задание 9 № 564542
На рисунке изображён график функции вида
где числа a, b, c, d — целые числа . Найдите
11 слайд

c
График перевернули и растянули в 2 раза, следовательно а=-2,
смещения вдоль оси ОХ нет, значит с=0, перенесли вдоль оси ОУ
вниз на 1, d=-1
12 слайд

Мы получили, что а=-2; с=0; d=-1
Найдём период функции:

Получили, что период =, а по графику период равен 2, следовательно
Искомая функция принимает вид:
13 слайд

2. Задание 9 № 564554
На рисунке изображён график функции вида
где числа a, b, c, d — целые числа . Найдите 𝑓 𝑓 17 3

График растянули в 2 раза, а=2
Относительно ОУ не смещали, с=0
Перенесли вверх на 2 единичных отрезка, d=2
Искомая функция принимает вид:
𝒇 𝒙 =𝟐 𝒄𝒐𝒔 𝝅𝒙 𝒃 +𝟐
14 слайд

Мы получили, что а=-2; с=0; d=-1
Найдём период функции:

Получили, что период =, а по графику период равен 2, следовательно
Искомая функция принимает вид:
15 слайд

График растянули в 2 раза, а=2
Относительно ОУ не смещали, с=0
Перенесли вверх на 2 единичных отрезка, d=2
Искомая функция принимает вид:
𝒇 𝒙 =𝟐 𝒄𝒐𝒔 𝝅𝒙 𝒃 +𝟐

Задание 9 № 564555
На рисунке изображён график функции вида
где числа a, b, c и d — целые. Найдите
16 слайд

Мы получили, что а=4; с=0; d=4
Найдём период функции:

Получили, что период =, а по графику период равен 4, следовательно
Искомая функция принимает вид:
17 слайд

1. Задание 9 № 564586
На рисунке изображён график функции вида
где числа a, b, c, d — целые числа . Найдите

Мы получили, что а=3; с=0; d=1

Найдём период функции:
18 слайд

Получили, что период равен, а по графику период равен 1,

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 156 856 материалов в базе

Выберите категорию:
Выберите учебник и тему

Выберите класс:
Тип материала:
- Все материалы
- Статьи
- Научные работы
- Видеоуроки
- Презентации
- Конспекты
- Тесты
- Рабочие программы
- Другие методич. материалы

Найти материалы

Материал подходит для УМК

«Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.

Тема

Глава 7. Тригонометрические функции

Больше материалов по этой теме

Другие материалы

Рейтинг:
5 из 5

01.12.2021
1454
495

01.12.2021
177
4

Рабочая программа по алгебре

Учебник: «Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
Тема: Глава 1. Выражения, тождества, уравнения

30.11.2021
92
0

30.11.2021
164
2

Вам будут интересны эти курсы:

Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Правовое обеспечение деятельности коммерческой организации и индивидуальных предпринимателей»
Курс повышения квалификации «Педагогическая риторика в условиях реализации ФГОС»
Курс повышения квалификации «Экономика предприятия: оценка эффективности деятельности»
Курс профессиональной переподготовки «Клиническая психология: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Основы построения коммуникаций в организации»
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
Курс профессиональной переподготовки «Организация деятельности помощника-референта руководителя со знанием иностранных языков»
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
Курс профессиональной переподготовки «Стратегическое управление деятельностью по дистанционному информационно-справочному обслуживанию»

Источник

: ЕГЭ по математике профиль

Новые задания №9 ЕГЭ 2022 по профильной математике — графики функций.

Для успешного результата необходимо уметь выполнять действия с функциями.

Задание №9 ЕГЭ 2022 математика профильный уровень Прототипы

Скачать задания	Источник
Новые задания 9	ФИПИ
Прототипы задания №9	vk.com/mathegeexam
Скачать задания	vk.com/ekaterina_chekmareva
→ Теория → Задачи → Шпаргалка	vk.com/abel_mat
Линейная функция	math100.ru
Парабола
Гипербола
Логарифмическая и показательная функции
Иррациональные функции
Тригонометрические функции

Из кодификатора 2022 года для выполнения 9 задания нужно изучить основные элементарные функции, их свойства и графики:

3.3.1 Линейная функция, её график

3.3.2 Функция, описывающая обратную пропорциональную зависимость, её график

3.3.3 Квадратичная функция, её график

3.3.4 Степенная функция с натуральным показателем, её график

3.3.5 Тригонометрические функции, их графики

3.3.6 Показательная функция, её график

3.3.7 Логарифмическая функция, её график

Уметь выполнять действия с функциями: определять значение функции по значению аргумента при различных способах задания функции; описывать по графику поведение и свойства функции, находить по графику функции наибольшее и наименьшее значения; строить графики изученных функций:

При отработке данного задания будут полезны книги:

Купить ЕГЭ. Математика. Графики функций, уравнения и неравенства, содержащие переменную под знаком модуля

Купить Задачи с параметрами. Применение свойств функций, преобразование неравенств

Связанные страницы:

Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи в разделе контакты

Источник

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения $frac{2,88cdot 44,5}{0,288cdot 4,45}.$

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

$frac{2,88cdot 44,5}{0,288cdot 4,45}=frac{2,88cdot 44,5}{2,88cdot 0,445}=frac{44,5}{0,445}=100.$

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения $7frac{9}{13}:frac{5}{13}.$

$7frac{9}{13}:frac{5}{13}=frac{100}{13}cdot frac{13}{5}=20.$

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

$left ( sqrt{a} right )^{2}=a;;sqrt{a}geq 0;;ageq 0$ .

3. Вычислите .

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:

Упростим множители:

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7} right )^{2}+2sqrt{3}cdot sqrt{7}+left ( sqrt{3} right )^{2}}=$

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7}+sqrt{3}right )^{2}}=2left ( sqrt{7}-sqrt{3} right )left ( sqrt{7}+sqrt{3} right )=$

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

$a^{m}cdot a^{n}=a^{m+n}.$

$frac{a^{m}}{a^{n}}=a^{m-n}.$

$left ( a^{m} right )^{n}=left ( a^{n} right )^{m}=a^{mn}.$

$a^{n}b^{n}=left ( ab right )^{n}.$

$frac{a^{n}}{b^{n}}=left ( frac{a}{b} right )^{n}.$

5. Найдите значение выражения: $frac{a^{8,9}}{a^{4,9}}$ при a=4.

$frac{a^{8,9}}{a^{4,9}}=a^{8,9-4,9}=a^{4}=4^{4}=256.$

Применили формулу частного степеней $frac{a^{m}}{a^{n}}=a^{m-n}.$

Ответ: 256.

6. Вычислите $left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}.$

$left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}=left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{2^{frac{1}{12}}} right )^{2}=left ( 2^{frac{1}{3}+frac{1}{4}-frac{1}{12}} right )^{2}=left ( 2^{frac{4}{12}+frac{3}{12}-frac{1}{12}} right )^{2}=$

$=left (2^{frac{1}{2}} right )^{2}=2.$

Ответ: 2.

7. Вычислите $frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}$ , если .

Спокойно, не пугаемся. И конечно, не спешим подставлять значение m=3,7. Сначала упростим выражение.

$frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}=frac{5m^{30}+13m^{30}}{4m^{30}}=frac{18m^{30}}{4m^{30}}=4,5.$

Ответ: 4,5.

8. Вычислите $0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}.$

$0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}=left ( frac{3}{4} right )^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot left ( 3cdot 4 right )^{frac{7}{8}}=frac{3^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 3^{frac{7}{8}}cdot 4^{frac{7}{8}}}{4^{frac{1}{8}}}=3cdot 4=12.$

Применили формулу для произведения степеней: $a^{m}cdot a^{n}=a^{m+n}.$

Ответ: 12.

9. Вычислите $frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}.$

$frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}=frac{3^{frac{1}{28}}cdot 3cdot 3^{frac{1}{21}}}{3^{frac{1}{12}}}=3^{frac{1}{28}+1+frac{1}{21}-frac{1}{12}}=3^{frac{3}{84}+1+frac{4}{84}-frac{7}{84}}=3.$

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

$log _{a}b=cLeftrightarrow a^{c}=b$ .

При этом > 0, > 0, aneq 1.

Основные логарифмические формулы:

Основное логарифмическое тождество: $boldsymbol{log _{a}a^{c}=c, ; a^{log _{a}b}=b}.$

Логарифм произведения равен сумме логарифмов: $boldsymbol{log _{a}left ( bc right )=log _{a}b+log _{a}c}.$

Логарифм частного равен разности логарифмов: $boldsymbol{log _{a}left ( frac{b}{c} right )=log _{a}b-log _{a}c}.$

Формула для логарифма степени: $boldsymbol{log _{a}b^{m}=mlog_{a}b}.$

Формула перехода к новому основанию: $boldsymbol{log _{a}b=frac{1}{log _{b}a},; log _{a}b=frac{log _{c}b}{log _{c}a}}.$

10. Вычислите: $log _{5}7cdot log _{7}25$ .

$log _{5}7cdot log _{7}25=log _{5}7cdot log _{7}5^{2}=2log _{5}7cdot log _{7}5=2.$

Снова формула перехода к другому основанию.

$log _{a}b=frac{1}{log _{b}a}$ , поэтому
$log _{a}bcdot log _{b};a=1.$

11. Найдите $log _{a}frac{a^{6}}{b^{4}}$ , если $log _{a}b=-2$ .

$log _{a}frac{a^{6}}{b^{4}}=log _{a}a^{6}-log _{a}b^{6}=6-4log _{a}b=6-4cdot left ( -2 right )=6+8=14.$

12. Найдите значение выражения $frac{log _{2}80}{3+log _{2}10}$ .

$frac{log _{2}80}{3+log _{2}10}=frac{log _{2}left (8cdot 10 right )}{3+log _{2}10}=frac{log _{2}8+log _{2}10}{3+log _{2}10}=frac{3+log _{2}10}{3+log _{2}10}=1.$

13. Найдите значение выражения $frac{log _{9}sqrt[10]{8}}{log _{9}8}$ .

$frac{log _{9}sqrt[10]{8}}{log _{9}8}=frac{log _{9}8^{frac{1}{10}}}{log _{9}8}=frac{1}{10}=0,1$ .

14. Найдите значение выражения $left ( 1-log _{3}18 right )left ( log _{6}54 -1right )$ .

$left ( 1-log _{3}18 right )left ( log _{6}54 -1right )=-left ( log _{3}18-log _{3}3 right )cdot left ( log _{6}54-log _{6}6 right )=-log _{3}6cdot log _{6}9=-2log _{3}6cdot log _{6}3=-2.$

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите: $44sqrt{3}tgleft ( -480^{circ} right ).$

$44sqrt{3}tgleft ( -480^{circ} right )=44sqrt{3}cdot frac{sin left ( -480^{circ} right )}{cos left ( -480^{circ} right )}=-44sqrt{3}cdot frac{sin 480^{circ}}{cos 480^{circ}}=-44sqrt{3}cdot frac{sin 120^{circ}}{cos 120^{circ}}=-44sqrt{3}cdot frac{sqrt{3}}{2}:left ( -frac{1}{2} right )=132.$

16. Найдите , если $sin alpha =-frac{2sqrt{2}}{3}$ и $alpha in left ( frac{3pi }{2};;2pi right )$ .

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{2sqrt{2}}{3} right )^{2}=1-frac{8}{9}=frac{1}{9}.$

Т.к. $alpha in left ( frac{3pi }{2};;2pi right )$ , то $cos alpha =frac{1}{3}.$
$3cos alpha =3cdot frac{1}{3}=1.$

17. Найдите , если $sin alpha =-frac{1}{sqrt{5}}$ и

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{1}{sqrt{5}} right )^{2}=1-frac{1}{5}=frac{4}{5}.$

Т.к. , то
$cos alpha =frac{2}{sqrt{5}}.$

$tgalpha =frac{sin alpha }{cos alpha }=-frac{1}{sqrt{5}}:frac{2}{sqrt{5}}=-2.$

18. Найдите значение выражения: $frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}.$

$frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{13cdot 2sin 76^{circ}cdot cos 76^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{26sin 76^{circ}}{cos 14^{circ}}=frac{26sin left ( 90^{circ}-14^{circ} right )}{cos 14^{circ}}=$

$=frac{26cos 14^{circ}}{cos 14^{circ}}=26.$

Применили формулу приведения.

19. Упростите выражение: $frac{3cos(pi - beta)+sin(frac{pi}{2}+beta)}{cos(beta+3pi)}.$

$frac{3cos left ( pi -beta right )+sin left ( frac{pi }{2}+beta right )}{cos left ( beta +3pi right )}=frac{-3cos beta +cos beta }{-cos beta }=frac{-2cos beta }{-cos beta }=2.$

Применили формулу приведения.

20. Найдите , если .

$2cos 2alpha =2left ( 1-2sin ^{2}alpha right )=2-4sin ^{2}alpha =2-4cdot left ( -0,7 right )^{2}=0,04.$

21. Вычислите $frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }$ , если

$frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }=frac{1-cos ^{2}alpha +sin ^{2}alpha +2sin alpha cos alpha }{1+cos ^{2}alpha -sin ^{2}alpha +2sin alpha cos alpha }=$

$=frac{2sin ^{2}alpha +2sin alpha cos alpha }{2cos ^{2}alpha +2sin alpha cos alpha }=frac{sin alpha left ( sin alpha +cos alpha right )}{cos alpha left ( cos alpha +sin alpha right )}=frac{sin alpha }{cos alpha }=tgalpha =0,3.$

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти $sqrt{a^{2}}$ .

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}$ при .

Запомним: $sqrt{a^{2}}=left | a right |.$

$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}=left | a-2 right |+left | a-4 right |$ .

Если , то и .

При этом и .

При получаем: .

Ответ: 2.

23. Найдите значение выражения

$x+sqrt{x^{2}-24x+144}$ при xleq 12 .

При xleq 12 получим:

$x+sqrt{x^{2}-24x+144}=x+sqrt{left ( x-12 right )^{2}}=x+left | x-12 right |=x+12-x=12.$

Ответ: 12.

24. Найдите $frac{gleft ( 5-x right )}{gleft ( 5+x right )}$ , если , при .

Что такое ? Это функция, каждому числу ставящая в соответствие число . Например, ;

Тогда:

Заметим, что .

Значит, при
$frac{gleft ( 5-x right )}{gleft ( 5+x right )}=1$ .

25. Найдите $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ , если $pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ , при .

$pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ — функция, каждому числу b ставящая в соответствии число
$left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ .

Тогда при bneq 0.

$pleft ( frac{1}{b} right )=left ( frac{1}{b}-9b right )left ( -frac{9}{b} +bright )=left ( b-frac{9}{b} right )left (-9b +frac{1}{b} right )=pleft ( b right )$ , и значение выражения $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ равно 1.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Слайд 1

Решение заданий ЕГЭ нового типа № 9 Анализ графиков

Слайд 2

Линейная функция f(x) = kx+b f (12) -? k = tg x = График функции проходит через точку с координатами (4;1) 1= * 4+ b 1= 1,5+b b= — 0,5 f(12) = x-0,5= *12 — 0,5 = 4

Слайд 3

Парабола y= y=a(x — m m – абсцисса вершины параболы n – ордината вершины параболы Коэффициент а отвечает за «расширение» или «сжатие» ветвей параболы. Чем больше |a|, тем «уже» парабола, чем меньше | a| , тем «шире» парабола. f(x) = f (-1) = (- 1 -5

Слайд 4

Гипербола График функции имеет вертикальную асимптоту х = 1, значит а = 1. График проходит через точку с координатами (2;1) 1 = k = 3 f(x) = f(19) =

Слайд 5

Гипербола Преобразуем функцию (выделим целую часть) kx+a x+b — kx+kb k f(x) = k + a-kb График имеет горизонтальную асимптоту y = 1, значит к=1

Слайд 6

Гипербола k – горизонтальная асимптота b – вертикальная асимптота y = — 2 k = -2

Слайд 7

Логарифмическая функци я График f(x) = log a x проходит через точку с координатами (1;0). График f(x) = b + log a x получается сдвигом графика f(x) = log a x вдоль оси ОУ вниз на 2 единичных отрезка, значит b = -2. График функции проходит через точку (3;1). -1 = -2 + а = 3 f(27) = — 2 + = -2+3 = 1

Слайд 8

Показательная функция График f(x) = проходит через точку с координатами (0;1). График f(x) = + b получается сдвигом графика у = вдоль оси ОУ вниз на 4 единичных отрезка, значит b = -4. График функции проходит через точку (-3;4). 4 = = 8 а = а = f (-5) = — 4 = 32 – 4 = 28

Слайд 9

Иррациональная функция График функции f (x) = a проходит через точку (4; 5 ). 5 = a a = 2 ,5 f (x) = 2 ,5 g (x) = kx + b, b = -2 k = tg α = g (x) = 2,5 = 10 = 3x – 8 100 x = 9 9 D = — 64 *9 = (74 – 8*3) (74 + 8*3) = 50*98

Слайд 10

Тригонометрические функции Множеством значений y = cos x является отрезок [ — 1; 1]. График расположен в промежутке между прямыми у = -1 и у = 1. 1 способ: 8 : 4 = 2 => а = 2 2 способ: |a| = => а = 2 3 способ: график проходит через точки с координатами (0 ; 1,5) и ( π ; — 2,5) a = 2

Источник

ЕГЭ Профиль №9. Тригонометрические функции

ЕГЭ Профиль №9. Тригонометрические функции

Описание презентации по отдельным слайдам:

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Тема

Другие материалы

Вам будут интересны эти курсы:

Новое и интересное на сайте: