СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий
Задания 12. Уравнения. Тригонометрические уравнения
Пройти тестирование по 10 заданиям
Пройти тестирование по всем заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 507595
а) Решите уравнение
б) Найдите корни этого уравнения, принадлежащие промежутку
Аналоги к заданию № 507595: 500917 501709 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 12 № 510018
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Источник: Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень.
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
3
Тип 12 № 504543
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 504543: 504564 507292 510671 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
4
Тип 12 № 500366
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 500366: 500587 501482 514505 Все
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
4 комментария · Сообщить об ошибке · Помощь
5
Тип 12 № 509579
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Аналоги к заданию № 509579: 509926 509947 509968 515762 519665 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
ЕГЭ Профиль №13. Тригонометрические уравнения
Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.
13 задания профильного ЕГЭ по математике представляет собой уравнение с отбором корней принадлежащих заданному промежутку. Одним из видов уравнений которое может оказаться в 13 задание является тригонометрическое уравнение. Как правило, это достаточно простое тригонометрическое уравнение для решения которого потребуется знания основных тригонометрических формул, и умение решать простейшие тригонометрические уравнения. Отбор корней тригонометрического уравнения принадлежащих заданному промежутку можно производить одним из четырех способов: методом перебора, с помощью тригонометрической окружности, с помощью двойного неравенства и графическим способом. В данном разделе представлены тригонометрические уравнения (всего 226) разбитые на три уровня сложности. Уровень А — это простейшие тригонометрические уравнения, которые являются подготовительными для решения реальных тригонометрических уравнений предлагаемых на экзамене. Уровень В — состоит из уравнений, которые предлагали на реальных ЕГЭ и диагностических работах прошлых лет. Уровень С — задачи повышенной сложности.
ЕГЭ (ПУ-5) Тригонометрические уравнения. Тренировочные задания.
учебно-методический материал по алгебре (10 класс) на тему
Задания открытого банка ЕГЭ по математике. Профильный уровень.
Скачать:
| Вложение | Размер |
|---|---|
| 1.2_ege_profil_zadanie_5._trigonometricheskie_uravneniya._trenirovochnye_zadaniya.doc | 198.5 КБ |
Предварительный просмотр:
ЕГЭ (профиль) Задание 5. Тригон. ур-ния.(Тренировочные задания.)
1. Решите уравнение. В ответе запишите наименьший положительный и наибольший отрицательный корень:
ЕГЭ (профиль) Задание 5. Тригон. ур-ния.(Тренировочные задания.)
1. Решите уравнение. в ответе запишите наименьший положительный и наибольший отрицательный корень:
ЕГЭ (профиль) Задание 5. Тригон. ур-ния.(Тренировочные задания.)
1. Решите уравнение. в ответе запишите наименьший положительный и наибольший отрицательный корень:
ЕГЭ (профиль) Задание 5. Тригон. ур-ния.(Тренировочные задания.)
1. Решите уравнение. в ответе запишите наименьший положительный и наибольший отрицательный корень:
По теме: методические разработки, презентации и конспекты
Неполные квадратные уравнения, тренировочные задания
Данная презентация может быть полезна при подготовке учащихся 9 классов К КДР и ГИА.
Конспект урока по теме: ”Тригонометрические уравнения. Решение простейших тригонометрических уравнений вида sinx = a. “
Разобраны свойства функции sinx. Приведено решение уравнения sinx=a. Разобраны 4 примера.
Тематический тренажер для подготовки к ГИА в 2014 г. по математике 9 класс. Тематические тренировочные задания. Отработка заданий: модуль «Алгебра» Тема№2 «Решение линейных уравнений»
Представляю вашему вниманию очередной тематический тренажер для подготовки к ГИА в 2014г по алгебре по теме «Решение линейных уравнений». Подобраны упражнения, которые соответствуют типовым заданиям К.
Тема 17. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. Решение простейших тригонометрических уравнений. Общий приём. Метод разложения на множители.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э.
Тема 17. ТРИГОНОМЕТРИЧЕСКИЕ УРАВНЕНИЯ. Решение простейших тригонометрических уравнений. Общий приём. Метод разложения на множители.
Уважаемые коллеги!Актуальной задачей на сегодняшний день является качественная подготовка учащихся к единому государственному экзамену (ЕГЭ) по математике, а также абитуриентов к вступительным э.
Тренировочные задания по теме:»Тригонометрические функции»
Тренировочные задания на вычисление значений тригонометрических функций.
ЕГЭ (ПУ-9) Тригонометрические тождества. Тренировочные задания.
Задания Открытого банка ЕГЭ по математике (профильный уровень).
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac<3pi >2;,3pi right].
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
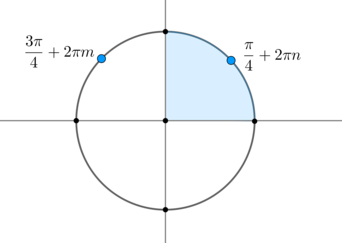
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac<3pi >2;, 3pi right].
x_1=fracpi 4+2pi =frac<9pi >4,
x_2=fracpi 3+2pi =frac<7pi >3,
x_3=-fracpi 3+2pi =frac<5pi >3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac<5pi >3, frac<7pi >3, frac<9pi >4.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac<3pi >2right] ;
Решение
а) ОДЗ: begin tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin 2 sin ^2 4x-3 cos 4x=0,\tg x=0. endright.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
t_1=frac12, t_2=-2, t_2notin [-1; 1].
4x=pm fracpi 3+2pi n,
x=pm fracpi <12>+frac<pi n>2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi <12>+pi n, n in mathbb Z; x=frac<5pi ><12>+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac<3pi >2right].
Ответ
а) pi k, k in mathbb Z; fracpi <12>+pi n, n in mathbb Z; frac<5pi ><12>+pi m, m in mathbb Z.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac<7pi >2;,frac<9pi >2right].
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_<1,2>=frac<1pmsqrt 9>4=frac<1pm3>4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac<2pi >3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac<11pi >3, x_2=4pi , x_3 =frac<13pi >3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac<11pi >3, 4pi , frac<13pi >3.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac<3pi >2-xright) ><1+tgx>.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac<3pi >2right).
Решение
а) 1. Согласно формуле приведения, ctgleft( frac<3pi >2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac<11+5tgx><1+tgx>.
Заметим, что frac<11+5tgx><1+tgx>= frac<5(1+tgx)+6><1+tgx>= 5+frac<6><1+tgx>, поэтому уравнение принимает вид: 5+5 cos x=5 +frac<6><1+tgx>. Отсюда cos x =frac<dfrac65><1+tgx>, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac<3sqrt 2>5. Значит, x-fracpi 4= arccos frac<3sqrt 2>5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac<3sqrt 2>5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac<3sqrt 2>5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac<3sqrt 2>5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac<3sqrt 2>5 и b=fracpi 4-arccos frac<3sqrt 2>5.
1. Докажем вспомогательное неравенство:
Заметим также, что left( frac<3sqrt 2>5right) ^2=frac<18> <25>значит frac<3sqrt 2>5
2. Из неравенств (1) по свойству арккосинуса получаем:
Отсюда fracpi 4+0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac<3sqrt 2>5,, b-2pi =-frac74pi -arccos frac<3sqrt 2>5Bigg). При этом -2pi
-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac<3pi >2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac<7pi >2.
Ответ
а) fracpi4pm arccosfrac<3sqrt2>5+2pi k, kinmathbb Z;
б) -frac<7pi>4pm arccosfrac<3sqrt2>5.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Решение
а) Преобразуем уравнение:
cos x+2 sin x cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Задание №1174
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac<3pi ><2>; -frac<pi >2 right].
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1<1+cos 2x>=frac 1<1+cos (pi +x)>, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 ,
2) -frac<3pi >2 leqslant -frac pi 3+2pi n leqslant -frac pi
3) -frac<3pi >2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac<11>6 leqslant 2m leqslant -frac56 , -frac<11> <12>leqslant m leqslant -frac5<12>.
Нет целых чисел, принадлежащих промежутку left [-frac<11><12>;-frac5<12>right] .
2) -frac <3pi>2 leqslant -frac<pi >3+2pi n leqslant -frac<pi ><2>, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1<6>, -frac7 <12>leqslant n leqslant -frac1<12>.
Нет целых чисел, принадлежащих промежутку left[ -frac7 <12>; -frac1 <12>right].
3) -frac<3pi >2 leqslant pi +2pi kleqslant -frac<pi >2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
Решение тригонометрического уравнения. Задание 5
Решение тригонометрического уравнения. Задание 5
В этой статье я покажу решение тригонометрического уравнения из Задания 5:
Задание 5 (№ 12889)
Найдите корень уравнения 
Рекомендую вам сначала вспомнить, как решаются простейшие тригонометрические уравнения, затем попробовать решить задачу самостоятельно и сверить свое решение с ВИДЕОУРОКОМ:
И еще одно видео на эту тему:
И.В. Фельдман, репетитор по математике.
источники:
http://academyege.ru/theme/trigonometricheskie-uravneniya-3.html
http://ege-ok.ru/2012/05/22/reshenie-trigonometricheskogo-uravneniya-zadanie-5
Методический центр сектора
дошкольного, общего и дополнительного образования
Муниципального бюджетного
учреждения
«Городское управление народного
образования»
ТРИГОНОМЕТРИЯ
ДЛЯ
УЧАЩИХСЯ
10-11
КЛАССОВ
Составитель:
Колобова С.А.,
учитель математики
МБОУ «Гимназия №2»
Инта
2014
Данная работа может быть
использована в качестве учебного материала при подготовке учащихся к экзамену.
В данной работе рассмотрены решения простейших тригонометрических уравнений. Рассмотрены
основные методы решения тригонометрических уравнений, показаны способы отбора
корней.
I.
Важные моменты при решении тригонометрических уравнений.
При решении
тригонометрических уравнений необходимо уметь вычислять значения арксинуса,
арккосинуса, арктангенса и арккотангенса. Это возможно вычислять с помощью
таблицы или единичной окружности.
Примеры использования единичной
окружности.
|
arcsin |
arcsin( arctg (-1) = |
|
аrcsin(- |
аrcsin 0 = 0 arccos arcctg 0 = не существует |
Тренировку по нахождению значений
арксинуса, арккосинуса, арктангенса и арккотангенса можно провести, используя
следующую таблицу.
|
1 |
2 |
3 |
4 |
|
arcsin |
|
|
arcsin |
|
arccos |
|
|
arcos |
|
arctg |
|
arctg |
|
|
|
arcctg |
|
arcctg |
|
|
|
|
|
|
|
|
|
arccos |
|
|
|
|
arctg |
|
|
|
arcctg |
|
Для успешного решения
тригонометрических уравнений необходимо знать основные формулы.
При решении
тригонометрических уравнений (для упрощения тригонометрических выражений) иногда
приходится использовать формулы приведения.
Тренировку можно
произвести с помощью следующей таблицы.
|
Упростить |
Вычислить |
Упростить |
Вычислить |
|
|
sin |
tg |
cos |
|
sin |
cos |
ctg |
tg |
|
cos |
sin |
sin |
ctg |
|
|
cos |
|
tg |
|
sin |
tg |
cos |
cos |
|
cos |
sin |
cos |
cos |
|
|
cos |
tg |
sin |
|
tg |
cos |
ctg |
cos |
II.
Решение простейших тригонометрических уравнений.
Для удобства запоминания формул можно
использовать следующую таблицу.
Частные случаи решения тригонометрических
уравнений.
Примеры решения простейших
тригонометрических уравнений.
|
или x=(-1)n |
или х = х = |
|
|
|
III.
Методы решения тригонометрических уравнений.
Решение
тригонометрического уравнения состоит из двух этапов: преобразование уравнения
для получения его простейшего вида ( см. выше ) и решение полученного
простейшего тригонометрического уравнения. Существует семь основных методов
решения тригонометрических уравнений.
1.Приведение к квадратному уравнению.
Ответ: +
; =
+
.
2.Приведение к однородному уравнению.
Уравнение
называется однородным относительно sin и cos, если все его члены одной и той
же степени относительно sin и cos одного и того же угла.
Чтобы
решить однородное уравнение, надо:
а) перенести все его члены в левую часть;
б) вынести все общие множители за скобки;
в) приравнять все множители и скобки нулю;
г) скобки, приравненные нулю, дают однородное уравнение меньшей степени,
которое следует разделить на cos ( или sin ) в старшей степени;
д) решить полученное алгебраическое уравнение относительно тангенса или
котангенса.
3sin2 x
+ 4 sin x · cos x + 5 cos2 x = 2.
3sin2 x + 4 sin x · cos x + 5 cos2
x = 2sin2 x + 2cos2 x ,
sin2
x
+ 4 sin x
· cos x
+ 3 cos2
x
= 0 , разделим обе части уравнения на cos2x
tg2x+4tgx+3=0,
пусть tgx=t,
тогда t2+4t+3=0.
Корнями этого уравнения являются числа
-1 и -3.
Если t=-1,
то tgx=-1,
x=
х =+
.
Если t=-3,
то tgx=-3,
x=
х =arctg(-3)+.
Ответ: +
; arctg(-3)+
.
3. Разложение на множители.
a)
sin2x—cosx=0,
2sinxcosx-cosx=0,
cosx(2sinx-1)=0,
cosx=0 или
2sinx-1=0
x=+
sinx=
x=(-1)karcsin+
x=(-1)k
Ответ: +
;
(-1)k
.
b)
sinx+cosx=sinxcosx+1,
sinx+cosx—sinxcosx-1=0,
sinx(1- cosx)+( cosx-1)=0,
( cosx-1)( sinx-1)=0
cosx-1=0 или
sinх-1=0
cosx=1 sinx=1
x=2 x=
+
Ответ: ;
+
.
4. Введение
вспомогательного угла.
sinx+cosx=2
разделим обе части уравнения на 2, получим
так
как cos=
и
sin=
sinx cos+
cosx sin=1 воспользуемся
формулой sinx cosy+
cosx siny=
sin(x+y)
sin(x+)=1, x+
=
+
, x=
+
+
, x=
+
.
Ответ: +
.
IV.
Отбор корней тригонометрического уравнения.
При
выполнении задания С-1 необходимо найти те корни уравнения, которые принадлежат
заданному промежутку. Это можно сделать с помощью перебора или решения
неравенства.
1.Решить уравнение:
2,5sin2x = 7 cos2 x – 1,
Найти все корни
уравнения, принадлежащие отрезку х .
В данном уравнении
отбор корней проведем перебором.
Для решения
уравнения воспользуемся основным тригонометрическим формулой двойного угла для
синуса и основным тригонометрическим тождеством. Получим уравнение
5sinxcosx = 7cos2 x – sin2 x –
cos2 x, т.е.
sin2 x – 6cos2 x+ 5sinxcosx = 0
Разделим обе части уравнения на cos2
x. Получим tg2 x+ 5tgx – 6 = 0.
Пусть tgx = t, тогда t2+ 5t – 6
= 0, t = 1 или t = –6.
tgx = 1 или tg = –6;
x=+
или
x=arctg(-6)+.
Проведём
отбор корней, принадлежащих отрезку .
Если
n=0, то x=. Этот корень принадлежит рассматриваемому
промежутку.
Если
n=1, то x=. Этот корень тоже принадлежит рассматриваемому
промежутку.
Если
n=2, то x=. Ясно, что данный корень не принадлежит
промежутку.
Если
n = –1, то x= – не принадлежит промежутку .
Если
k=0, то x=
arctg(-6), x=- arctg6– не
принадлежит промежутку .
Если
k=1, то x=
arctg(-6)+. Этот корень
принадлежит рассматриваемому промежутку.
Аналогично предыдущему случаю убедимся,
что при k
= 0 и k
= 2, а, следовательно, при k
= –1, –2,…k = 3,4,… мы получим
корни, не принадлежащие промежутку .
Ответ: a)
x=+
или
x=arctg(-6)+.
б);
; arctg(-6)+
.
2. Решить
уравнение sin2x-2
cos2x=2
и указать корни, принадлежащие промежутку .
Используя формулу
двойного угла косинуса и основное тригонометрическое тождеств. Получим
уравнение sin2x=1.
Тогда sinx=1
или sinx=-1.
х=+
х=
+
Проведём отбор корней, принадлежащих
отрезку .
Составим и решим неравенства:
+
1+
1+
целых значений m
удовлетворяющих неравенству нет.
+
1+
n=1 удовлетворяет неравенству.
Если
n=1, то х=
Ответ:
a) +
,k
б)
.
3.Необходимо
обратить внимание на уравнения, содержащие деление.
Решите уравнение: а)
. б) Найдите все корни этого уравнения
принадлежащие отрезку .
a) ,
,



. k
б
) Если k=0, то х=. Данный корень не принадлежит
промежутку.
Если
k=-1, то х=. Данный корень не принадлежит
промежутку.
Если k=-2,
то х=. Данный
корень принадлежит промежутку.
Если
k=-3,
то х=. Данный
корень принадлежит промежутку.
Ответ: a) k
. б)
,
.
5
.
07
Тригонометрические уравнения
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами — ЛЕГКО!
Подтемы раздела
решение уравнений
5.01Линейные и квадратные уравнения
5.02Кубические уравнения
5.03Рациональные уравнения
5.04Иррациональные уравнения (со знаком корня)
5.05Показательные уравнения (с неизвестной в показателе степени)
5.06Логарифмические уравнения
5.07Тригонометрические уравнения
5.08Уравнения с модулем
5.09Задачи повышенного уровня сложности
Решаем задачи
Решите уравнение
В ответе укажите сумму наименьших трех положительных корней уравнения, деленную на
Показать ответ и решение
Данное уравнение равносильно серии корней
Найдем положительные корни уравнения, решив неравенство:
Значит, первые три положительных корня получаются при и это
Следовательно, их сумма, деленная на равна
Решите уравнение. В ответе укажите деленный на наименьший положительный корень, принадлежащий первой
четверти.
Показать ответ и решение
Решениями уравнения являются две серии:
Видим, что в первой четверти лежит только серия Найдем наименьший положительный корень, решив
неравенство:
Тогда наименьшее целое при этом значении получаем корень
Следовательно, в ответ запишем
Решите уравнение. В ответе укажите сумму наименьшего положительного и наибольшего отрицательного корней
уравнения.
Показать ответ и решение
Данное уравнение равносильно двум сериям корней
Найдем положительные корни уравнения, решив неравенства:
Наименьшее подходящее целое — это
при нем получается
Наименьшее подходящее целое — это
при нем получается
При этом
Аналогично найдем наибольший отрицательный корень, он получается из второй серии корней при
Тогда сумма наименьшего положительного и наибольшего отрицательного корней равна
Решите уравнение
В ответе укажите наименьший положительный корень уравнения, деленный на
Показать ответ и решение
Данное уравнение равносильно серии корней
Найдем положительные корни уравнения, решив неравенство:
Наименьшее подходящее целое — это
при нем получается
Следовательно, в ответ пойдет
Решите уравнение В ответе укажите целый корень уравнения.
Показать ответ и решение
Данное уравнение равносильно серии корней
Заметим, что единственный целый корень из этой серии получается при и это
Все остальные корни будут вида
«целое число умножить на », что является иррациональным числом.
Найдите корни уравнения. В ответ запишите наименьший положительный
корень.
Показать ответ и решение
Наименьший положительный корень в первой серии равен при
Наименьший положительный корень во второй серии равен при
Выбираем
Найдите корни уравнения. В ответе напишите наибольший отрицательный
корень.
Показать ответ и решение
Таким образом, наибольший отрицательный корень получим при
Найдите наименьший положительный корень уравнения
Показать ответ и решение
Легко проверить, что при достигается наименьший положительный корень
Найдите наименьший корень уравнения
Показать ответ и решение
Наименьший корень достигается при наибольшем для которого знаменатель все еще отрицателен. Это
и
Найдите наименьший положительный корень уравнения
Показать ответ и решение
Легко проверить, что при достигается наименьший положительный корень
Найдите наибольший отрицательный корень уравнения
Показать ответ и решение
Легко проверить, что при достигается наибольший отрицательный корень
Найдите наименьший положительный корень уравнения
Показать ответ и решение
Легко проверить, что при достигается наименьший положительный корень
Решите уравнение
В ответе запишите наибольший отрицательный корень.
Показать ответ и решение
По определению синуса на тригонометрической окружности имеем две серии решений:
Значение каждого из корней увеличивается при увеличении При
получаем корни
и
при больших оба корня уже будут положительны. Значит, наибольший отрицательный корень равен
Найдите наибольший отрицательный корень уравнения
Показать ответ и решение
Значение корня увеличивается при увеличении При
получаем корень
при больших
корень
уже будет положителен. Значит, наибольший отрицательный корень равен
Найдите наибольший отрицательный корень уравнения
Показать ответ и решение
Значение корня увеличивается при увеличении При
получаем корень
при больших
корень уже
будет положителен. Значит, наибольший отрицательный корень равен
Ответ:
Найдите наибольший отрицательный корень уравнения
Показать ответ и решение
Ответ:
Найдите наибольший корень уравнения
Показать ответ и решение
Наибольший корень достигается при наименьшем для которого знаменатель все еще положителен. Это
и
Найдите наибольший отрицательный корень уравнения
Показать ответ и решение
Значение корня увеличивается при увеличении При
получаем корень
при больших
корень уже
будет положителен. Значит, наибольший отрицательный корень равен
Найдите наибольший отрицательный корень уравнения
Показать ответ и решение
Значение корня увеличивается при увеличении При
получаем корень
при больших
корень уже будет
положителен. Значит, наибольший отрицательный корень равен
Найдите корень уравнения. Если уравнение имеет более одного корня, в ответе укажите наименьший из его
положительных корней.
Показать ответ и решение
ОДЗ: – произвольное. Решим на ОДЗ:
Решение уравнения имеет вид:
Откуда для исходного уравнения получаем
что равносильно
– подходят по ОДЗ. Среди корней наименьший положительный
Задачи ЕГЭ профиль
а) Решите уравнение (2sin^2x-2sqrt2cos x+1=0)
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[ dfrac{5pi}{2};4piright]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π/2 | 18. 8π/3 | 19. 11π/4 | 20. 17π/6 |
| 21. 3π | 22. 19π/6 | 23. 13π/4 | 24. 10π/3 |
| 25. 7π/2 | 26. 11π/3 | 27. 15π/4 | 28. 23π/6 |
| 29. 4π |
а) Решите уравнение (8sin^2{x} + 2sqrt{3}cos{x} + 1 = 0).
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[-dfrac{7pi}{2}; -2piright]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17.-7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25. -5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π |
а) Решить уравнение (2cos 2x+4sqrt{3}cos x-7=0).
б) Найдите все корни этого уравнения, принадлежащие промежутку (left[dfrac{5pi}{2};4piright]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 5π/2 | 18. 8π/3 | 19. 11π/4 | 20. 17π/6 |
| 21. 3π | 22. 19π/6 | 23. 13π/4 | 24. 10π/3 |
| 25. 7π/2 | 26. 11π/3 | 27. 15π/4 | 28. 23π/6 |
| 29. 4π |
а) Решите уравнение (sin2x cos x+sin x cos2x=dfrac1{sqrt2}).
б) Найдите все его корни, принадлежащие отрезку (left[ dfrac{pi}6;piright]).
а) Решите уравнение (2cos^3{x}+sqrt{3}cos^2{x}+2cos{x}+sqrt{3}=0)
б) Укажите корни этого уравнения, принадлежащие отрезку (left[-2pi;-dfrac{pi}{2}right])
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -2π | 18. -11π/6 | 19. -7π/4 | 20. -5π/3 |
| 21. -3π/2 | 22. -4π/3 | 23. -5π/4 | 24. -7π/6 |
| 25. -π | 26. -5π/6 | 27. -3π/4 | 28. -2π/3 |
| 29. -π/2 |
а) Решите уравнение (dfrac1{cos^2x}-dfrac3{cos x}+2=0).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[ -3pi;-dfrac{3pi}{2}right]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -3π | 18. -17π/6 | 19. -11π/4 | 20. -8π/3 |
| 21. -5π/2 | 22. -7π/3 | 23. -9π/4 | 24. -13π/6 |
| 25. -2π | 26. -11π/6 | 27. -7π/4 | 28. -5π/3 |
| 29. -3π/2 |
а) Решите уравнение (6sin^2x-5sin x-4=0).
б) Найдите все корни этого уравнения, принадлежащие отрезку (left[ -dfrac{7pi}{2};-dfrac{3pi}2right]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17.-7π/2 | 18. -10π/3 | 19. -13π/4 | 20. -19π/6 |
| 21. -3π | 22. -17π/6 | 23. -11π/4 | 24. -8π/3 |
| 25.-5π/2 | 26. -7π/3 | 27. -9π/4 | 28. -13π/6 |
| 29. -2π | 30. -11π/6 | 31. -7π/4 | 32. -5π/3 |
а) Решите уравнение (2sin^2x-3sqrt3sinleft(dfrac{pi}{2}+xright)-5=0).
б) Укажите все корни этого уравнения, принадлежащие отрезку (left[-dfrac{5pi}{2};-pi right] ).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4.π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. -5π/2 | 18. -7π/3 | 19. -9π/4 | 20. -13π/6 |
| 21. -2π | 22. -11π/6 | 23. -7π/4 | 24. -5π/3 |
| 25. -3π/2 | 26. -4π/3 | 27. -5π/4 | 28. -7π/6 |
| 29. -π |
а) Решите уравнение (2sin^4{x} + 3cos{2x} +1 = 0).
б) Найдите все корни этого уравнения, принадлежащие отрезку ([pi; 3pi]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
а)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. π | 18. 7π/6 | 19. 5π/4 | 20. 4π/3 |
| 21. 3π/2 | 22. 5π/3 | 23. 7π/4 | 24. 11π/6 |
| 25. 2π | 26. 13π/6 | 27. 9π/4 | 28. 7π/2 |
| 29. 5π/2 | 30. 8π/3 | 31. 11π/4 | 32. 17π/6 |
а) Решите уравнение ( cos2x+sinleft(dfrac{pi}2-xright)+1=0).
б) Укажите корни этого уравнения, принадлежащие отрезку (Big[dfrac{3pi}{2}; 3piBig]).
Выберите все верные ответы на пункты а) и б). Запишите их номера по возрастанию, через запятую, без пробелов.
a)
| 1. 2πn, n∈Z | 2. π/6+2πn, n∈Z | 3. π/4+2πn, n∈Z | 4. π/3+2πn, n∈Z |
| 5. π/2+2πn, n∈Z | 6. 2π/3+2πn, n∈Z | 7. 3π/4+2πn, n∈Z | 8. 5π/6+2πn, n∈Z |
| 9. π+2πn, n∈Z | 10. -π/6+2πn, n∈Z | 11. -π/4+2πn, n∈Z | 12. -π/3+2πn, n∈Z |
| 13. -π/2+2πn, n∈Z | 14. -2π/3+2πn, n∈Z | 15. -3π/4+2πn, n∈Z | 16. -5π/6+2πn, n∈Z |
б)
| 17. 3π/2 | 18. 5π/3 | 19. 7π/4 | 20. 11π/6 |
| 21. 2π | 22. 13π/6 | 23. 9π/4 | 24. 7π/3 |
| 25. 5π/2 | 26. 8π/3 | 27. 11π/4 | 28. 17π/6 |
| 29. 3π |
Задание 788
Найдите корень уравнения: $$tg frac{pi x}{4}=-1$$. Если уравнение имеет более одного корня, в ответе запишите наибольший отрицательный
Ответ: -1
Задание 1173
Найдите корень уравнения $$ arccos x= frac{2pi }{3}$$
Ответ: -0.5
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Для того, чтобы решить данное уравнение $$ arccos x= frac{2pi }{3}$$, нам, фактически, надо указать абсциссу, которой соответствует точка $$frac{2pi }{3}$$ на единичной окружности. У этой точки координаты $$(-frac{1}{2};frac{sqrt{3}}{2})$$ $$ x = — frac{1}{2} $$
Задание 5095
Решите уравнение $$cosfrac{pi x}{6}=-0,5$$. В ответе запишите наибольший отрицательный корень уравнения.
Ответ: -4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$cos frac{pi x}{6}=-0,5Leftrightarrow$$ $$frac{pi x}{6}=pm frac{2 pi}{3}+2 pi n, n in ZLeftrightarrow$$ $$x=pm 4+12n, n in Z$$
Найдем наибольший отрицательный :
$$left{begin{matrix}4+12n<0\-4+12n<0end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}12n<-4\12<4end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}n<-frac{1}{3}\n<frac{1}{3}end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}n=-1\n=0 & &end{matrix}right.$$
$$x_{1}=4+12(-1)=-8$$, $$x_{2}=-4+12*0=-4$$
Наибольший отрицательный: -4.
Задание 6411
Найдите корень уравнения $$sin frac{pi(x+9)}{4}=-frac{sqrt{2}}{2}$$ . В ответе напишите наименьший положительный корень.
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Найдем значение х:
$$left[begin{matrix}frac{pi(x+9)}{4}=-frac{pi}{4} +2pi n , n in Z|:frac{pi}{4}\frac{pi(x+9)}{4}=-frac{3pi}{4} +2pi n , n in Zend{matrix}right.Leftrightarrow$$ $$left[begin{matrix}x+9=-1+8n\x+9=-3+8nend{matrix}right.Leftrightarrow$$ $$left[begin{matrix}x=-10+8n\x=-12+8n, n in Zend{matrix}right.$$
Найдем наименьший положительный для первого корня: $$-12+8n>0Leftrightarrow$$ $$8n>12Leftrightarrow$$ $$n>pm 1,5$$. Тогда, наименьшее n при котором выйдет наименьший положительный корень составит 2: При $$n=2: x=-12+8*2=4$$
Найдем наименьший положительный для второго корня:$$-10+8n>0Leftrightarrow$$ $$8n>10Leftrightarrow$$ $$n>1frac{1}{4}$$, тогда, наименьшее n при котором выйдет наименьший положительный корень составит 2: при n=2 $$x=-10+8*2=6$$
Как видим, наименьший положительный корень равен 4
Задание 9772
Найдите наименьший положительный корень уравнения $$cos^{4}frac{pi x}{4}=1+sin^{4} frac{pi x}{4}$$
Ответ: 4
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 10278
Найдите $$x_{0}$$ ‐ наибольший отрицательный корень уравнения $$sqrt{-3sin x+cos x}=sqrt{sin x-3cos x}$$. В ответе укажите $$frac{x_{0}}{pi}$$
Ответ: -0,75
Скрыть
Задание 14636
Решите уравнение $$2cos^2frac{pi x}{18}+5sinfrac{pi x}{18}=-1.$$ В ответе запишите наибольший отрицательный корень уравнения.
Ответ: -3
Скрыть
$$2(1-sin^2frac{pi x}{18})+5sinfrac{pi x}{18}+1=0$$
$$-2sin^2frac{pi x}{18}+5sinfrac{pi x}{18}+3=0$$
$$2sin^2frac{pi x}{18}-5sinfrac{pi x}{18}-3=0$$
$$frac{5pmfrac{7}{125+24}}{4}$$
$$left[begin{matrix} sinfrac{pi x}{18}=3; н.р.\ sinfrac{pi x}{18}=-frac{1}{2} end{matrix}right.$$
$$frac{pi x}{18}=(-1)^{k+1}cdotfrac{frac{1}{pi}}{6}+pi k$$
$$x=(-1)^{k+1}cdotfrac{18}{6}+18k$$
$$x=(-1)^{k+1}cdot3+18k$$
при $$k=0$$ $$x=-3$$
Задание 14826
Решите уравнение $$cosfrac{pi(x-7)}{3}=frac{1}{2}.$$ В ответе запишите наибольший отрицательный корень.
Ответ: -4
Скрыть
$$frac{pi(x-7)}{3}=pmfrac{pi}{3}+2pi n$$
$$x-7=pm1pm6n$$
$$left{begin{matrix} x=8+6n\ x=6+6n, nin Z end{matrix}right.$$
Заметим, что значениям $$ngeq0$$ соответствуют только положительные корни, поэтому они сразу отбрасываются. Теперь последовательно переберем отрицательные значения $$n,$$ получим:
— при $$n=-1$$ имеем $$x=2$$ и $$x=0;$$
— при $$n=-2$$ имеем $$x=8-12=-4$$ и $$x=6-12=-6;$$
— при $$nleq-3$$ корни будут убывать.
Таким образом, наибольший отрицательный корень равен $$-4.$$
Задание 15003
Решите уравнение $$sinfrac{pi(x+2)}{6}=frac{sqrt{3}}{2}.$$ В ответе укажите наибольший отрицательный корень.
Ответ: -10
Скрыть
$$sinfrac{pi(x+2)}{6}=frac{sqrt{3}}{2}$$
$$left[begin{matrix} frac{pi(x+2)}{6}=frac{pi}{3}+2pi n,nin Z\ frac{pi(x+2)}{6}=frac{2pi}{3}+2pi n end{matrix}right.Leftrightarrowleft[begin{matrix} x+2=2+12n,nin Z\ x+2=4+12n end{matrix}right.Leftrightarrowleft[begin{matrix} x=12n,nin Z\ x=2+12n end{matrix}right.$$
Пусть $$n=1$$: получим $$-12$$ и $$-10.$$ Пусть $$n=0$$: $$0$$ и $$2.$$
Тогда наибольший отрицательный $$-10$$
Задание 15234
Решите уравнение $$sinfrac{pi(5x-6)}{24}=frac{1}{2}.$$ В ответ запишите наибольший отрицательный корень уравнения.
Ответ: -4,4
Скрыть
$$sinfrac{pi(5x-6)}{24}=frac{1}{2}Leftrightarrowleft{begin{matrix} frac{pi(5x-6)}{24}=frac{pi}{6}+2pi n,nin Zquad|:frac{pi}{24}\ frac{pi(5x-6)}{24}=frac{5pi}{6}+2pi n,nin Zquad|:frac{pi}{24} end{matrix}right.Leftrightarrow$$
$$Leftrightarrowleft{begin{matrix} 5x-6=4+48n,nin Z |+6|:5\ 5x-6=20+48n end{matrix}right.Leftrightarrowleft{begin{matrix} x=2+9,6n,nin Z\ x=5,2+9,6n end{matrix}right.$$
При этом корень отрицательный и наибольший:
если $$n=0$$: $$2$$ и $$5,2$$
если $$n=-1$$: $$2-9,6=-7,6$$ и $$5,2-9,6=-4,4$$
Наибольший отрицательный $$-4,4.$$
Задание 15313
Решите уравнение $$sinfrac{pi(4x+7)}{6}=-frac{sqrt{3}}{2}.$$ В ответе запишите наименьший положительный корень.
Ответ: 0,25
Скрыть
$$frac{pi(4x+7)}{6}=-frac{pi}{3}+2pi n$$
$$frac{pi(4x+7)}{6}=-frac{2pi}{3}+2pi n$$
$$x=-frac{9}{4}+frac{12}{4}n$$
$$x=-frac{11}{4}+frac{12}{4}n$$
При $$n=0;1;2$$ получаем:
$$x=-frac{9}{4};frac{3}{4};frac{15}{4}$$
$$x=-frac{11}{4};frac{1}{4};frac{13}{4}$$
$$Rightarrow frac{1}{4}=0,25$$
Задание 15718
Решите уравнение $$sinfrac{pi x}{8}=frac{sqrt{2}}{2}.$$ В ответе запишите наибольший отрицательный корень уравнения.
Ответ: -2
Скрыть
$$frac{πx}{8}=−frac{π}{4}+2πn$$
$$frac{πx}{8}=−frac{3π}{4}+2πn$$
$$x=−2+16n$$
$$x=−6+16n$$
Наибольший отрицательный корень будет при $$n=0$$
$$x=−2$$
$$x=−6$$
Задание 15876
Решите уравнение $$cos(frac{pi x}{2}-frac{27pi}{16})=0$$
В ответе запишите наибольший отрицательный корень уравнения
Ответ: -1,625
Скрыть
$$frac{pi x}{2}-frac{27pi}{16}=frac{pi}{2}+pi n$$
$$frac{x}{2}-frac{27}{16}=frac{1}{2}+n$$
$$x=frac{35}{8}+2n$$
$$n=-3$$
$$x=4frac{3}{8}-6=-1,625$$
Задание 15899
Решите уравнение $$sinfrac{pi x}{12}=0,5$$. В ответе укажите наименьший из тех корней, которые больше 4.
Ответ: 10
Скрыть
$$sinfrac{pi x}{12}=0,5left[begin{matrix} frac{pi x}{12}=frac{pi}{6}+2pi n\ frac{pi x}{12}=frac{5pi}{6}+2pi n, nin Z end{matrix}right.Leftrightarrowleft[begin{matrix} x=2+24n\ x=10+24n, nin Z end{matrix}right.$$
$$2+24n>4Rightarrow 24n>2Rightarrow n>frac{1}{12}Rightarrow n=1: 2+24cdot1=26$$
$$10+24n>4Rightarrow 24n>-6Rightarrow n>-frac{1}{4}Rightarrow n=0: 10+24cdot0=10$$
Наименьший 10.
Задание 16263
Решите уравнение $$tgfrac{pi(x+1)}{3}=-sqrt{3}$$. В ответе укажите наименьший положительный корень.
Ответ: 1
Скрыть
$$tgfrac{pi(x+1)}{3}=-sqrt{3}Rightarrowfrac{pi(x+1)}{3}=-frac{pi}{3}+pi nRightarrow x+1=-1+3nRightarrow x=-2+3n$$
$$left{begin{matrix} -2+3n>0\ nto min \ nin Z end{matrix}right.Rightarrowleft{begin{matrix} n>frac{2}{3}\ nto min\ nin Z end{matrix}right.Rightarrow n=1:quad x=-2+3cdot1=1$$










.png)