СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Тригонометрические уравнения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 507595
а) Решите уравнение
б) Найдите корни этого уравнения, принадлежащие промежутку
Аналоги к заданию № 507595: 500917 501709 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 12 № 510018
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Источник: Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень.
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
3
Тип 12 № 504543
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 504543: 504564 507292 510671 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
4
Тип 12 № 500366
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 500366: 500587 501482 514505 Все
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
4 комментария · Сообщить об ошибке · Помощь
5
Тип 12 № 509579
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Аналоги к заданию № 509579: 509926 509947 509968 515762 519665 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
ЕГЭ Профиль №12. Тригонометрические уравнения
Прототипы задания №1 профильного ЕГЭ 2022 по математике
Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.
Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.
Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы
| Источник: math100.ru | → Рациональные уравнения
→ Тригонометрические уравнения |
| time4math.ru | → скачать задания |
| vk.com/ekaterina_chekmareva | → задания |
При отработке данного задания будут полезны книги:
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac<3pi >2;,3pi right].
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac<3pi >2;, 3pi right].
x_1=fracpi 4+2pi =frac<9pi >4,
x_2=fracpi 3+2pi =frac<7pi >3,
x_3=-fracpi 3+2pi =frac<5pi >3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac<5pi >3, frac<7pi >3, frac<9pi >4.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac<3pi >2right] ;
Решение
а) ОДЗ: begin tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin 2 sin ^2 4x-3 cos 4x=0,\tg x=0. endright.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
t_1=frac12, t_2=-2, t_2notin [-1; 1].
4x=pm fracpi 3+2pi n,
x=pm fracpi <12>+frac<pi n>2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi <12>+pi n, n in mathbb Z; x=frac<5pi ><12>+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac<3pi >2right].
Ответ
а) pi k, k in mathbb Z; fracpi <12>+pi n, n in mathbb Z; frac<5pi ><12>+pi m, m in mathbb Z.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac<7pi >2;,frac<9pi >2right].
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_<1,2>=frac<1pmsqrt 9>4=frac<1pm3>4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac<2pi >3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac<11pi >3, x_2=4pi , x_3 =frac<13pi >3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac<11pi >3, 4pi , frac<13pi >3.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac<3pi >2-xright) ><1+tgx>.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac<3pi >2right).
Решение
а) 1. Согласно формуле приведения, ctgleft( frac<3pi >2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac<11+5tgx><1+tgx>.
Заметим, что frac<11+5tgx><1+tgx>= frac<5(1+tgx)+6><1+tgx>= 5+frac<6><1+tgx>, поэтому уравнение принимает вид: 5+5 cos x=5 +frac<6><1+tgx>. Отсюда cos x =frac<dfrac65><1+tgx>, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac<3sqrt 2>5. Значит, x-fracpi 4= arccos frac<3sqrt 2>5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac<3sqrt 2>5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac<3sqrt 2>5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac<3sqrt 2>5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac<3sqrt 2>5 и b=fracpi 4-arccos frac<3sqrt 2>5.
1. Докажем вспомогательное неравенство:
Заметим также, что left( frac<3sqrt 2>5right) ^2=frac<18> <25>значит frac<3sqrt 2>5
2. Из неравенств (1) по свойству арккосинуса получаем:
Отсюда fracpi 4+0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac<3sqrt 2>5,, b-2pi =-frac74pi -arccos frac<3sqrt 2>5Bigg). При этом -2pi
-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac<3pi >2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac<7pi >2.
Ответ
а) fracpi4pm arccosfrac<3sqrt2>5+2pi k, kinmathbb Z;
б) -frac<7pi>4pm arccosfrac<3sqrt2>5.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Решение
а) Преобразуем уравнение:
cos x+2 sin x cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Задание №1174
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac<3pi ><2>; -frac<pi >2 right].
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1<1+cos 2x>=frac 1<1+cos (pi +x)>, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 ,
2) -frac<3pi >2 leqslant -frac pi 3+2pi n leqslant -frac pi
3) -frac<3pi >2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac<11>6 leqslant 2m leqslant -frac56 , -frac<11> <12>leqslant m leqslant -frac5<12>.
Нет целых чисел, принадлежащих промежутку left [-frac<11><12>;-frac5<12>right] .
2) -frac <3pi>2 leqslant -frac<pi >3+2pi n leqslant -frac<pi ><2>, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1<6>, -frac7 <12>leqslant n leqslant -frac1<12>.
Нет целых чисел, принадлежащих промежутку left[ -frac7 <12>; -frac1 <12>right].
3) -frac<3pi >2 leqslant pi +2pi kleqslant -frac<pi >2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
Тригонометрические уравнения и преобразования
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
Значения тригонометрических функций некоторых углов
| $α$ | $ 0$ | $<π>/<6>$ | $<π>/<4>$ | $<π>/<3>$ | $<π>/<2>$ | $π$ |
| $sinα$ | $ 0$ | $ <1>/<2>$ | $ <√2>/<2>$ | $ <√3>/<2>$ | $ 1$ | $ 0$ |
| $cosα$ | $ 1$ | $ <√3>/<2>$ | $ <√2>/<2>$ | $ <1>/<2>$ | $ 0$ | $ -1$ |
| $tgα$ | $ 0$ | $ <√3>/<3>$ | $ 1$ | $ √3$ | $ -$ | $ 0$ |
| $ctgα$ | $ -$ | $ √3$ | $ 1$ | $ <√3>/<3>$ | $ 0$ | $ -$ |
Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
Знаки тригонометрических функций по четвертям
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить, что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ ($<π>/<2>$ и $<3π>/<2>$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.
$сos(90° + α)= — sinα$ — это конечный результат преобразования
Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Тригонометрические тождества
- $tgα=/$
- $ctgα=/$
- $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
Вычислить $sin t$, если $cos t = <5>/ <13>; t ∈(<3π>/<2>;2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈(<3π>/<2>;2π)$ -это четвертая четверть, то синус в ней имеет знак минус
источники:
http://academyege.ru/theme/trigonometricheskie-uravneniya-3.html
http://examer.ru/ege_po_matematike/teoriya/trigonometricheskie_vyrageniya
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Стереометрия. Расстояния и углы в пространстве
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac{3pi }2;,3pi right].
Показать решение
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac{3pi }2;, 3pi right].
x_1=fracpi 4+2pi =frac{9pi }4,
x_2=fracpi 3+2pi =frac{7pi }3,
x_3=-fracpi 3+2pi =frac{5pi }3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac{5pi }3, frac{7pi }3, frac{9pi }4.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt {tgx}=0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac{3pi }2right] ;
Показать решение
Решение
а) ОДЗ: begin{cases} tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end{cases}
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin{array}{l} 2 sin ^2 4x-3 cos 4x=0,\tg x=0. end{array}right.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
2(1-t^2)-3t=0,
2t^2+3t-2=0,
t_1=frac12, t_2=-2, t_2notin [-1; 1].
cos 4x=frac12,
4x=pm fracpi 3+2pi n,
x=pm fracpi {12}+frac{pi n}2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1-я и 3-я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi {12}+pi n, n in mathbb Z; x=frac{5pi }{12}+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac{3pi }2right].
x=fracpi {12}, x=frac{5pi }{12}; x=pi ; x=frac{13pi }{12}; x=frac{17pi }{12}.
Ответ
а) pi k, k in mathbb Z; fracpi {12}+pi n, n in mathbb Z; frac{5pi }{12}+pi m, m in mathbb Z.
б) pi; fracpi {12}; frac{5pi }{12}; frac{13pi }{12}; frac{17pi }{12}.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac{7pi }2;,frac{9pi }2right].
Показать решение
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_{1,2}=frac{1pmsqrt 9}4=frac{1pm3}4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac{2pi }3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12.Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac{11pi }3, x_2=4pi , x_3 =frac{13pi }3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac{11pi }3, 4pi , frac{13pi }3.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac{11+5ctgleft( dfrac{3pi }2-xright) }{1+tgx}.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac{3pi }2right).
Показать решение
Решение
а) 1. Согласно формуле приведения, ctgleft( frac{3pi }2-xright) =tgx. Областью определения уравнения будут такие значения x, что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac{11+5tgx}{1+tgx}.
Заметим, что frac{11+5tgx}{1+tgx}= frac{5(1+tgx)+6}{1+tgx}= 5+frac{6}{1+tgx}, поэтому уравнение принимает вид: 5+5 cos x=5 +frac{6}{1+tgx}. Отсюда cos x =frac{dfrac65}{1+tgx}, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac{3sqrt 2}5. Значит, x-fracpi 4= arccos frac{3sqrt 2}5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac{3sqrt 2}5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac{3sqrt 2}5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac{3sqrt 2}5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac{3sqrt 2}5 и b=fracpi 4-arccos frac{3sqrt 2}5.
1. Докажем вспомогательное неравенство:
frac{sqrt 2}{2}<frac{3sqrt 2}2<1.
Действительно, frac{sqrt 2}{2}=frac{5sqrt 2}{10}<frac{6sqrt2}{10}=frac{3sqrt2}{5}.
Заметим также, что left( frac{3sqrt 2}5right) ^2=frac{18}{25}<1^2=1, значит frac{3sqrt 2}5<1.
2. Из неравенств (1) по свойству арккосинуса получаем:
arccos 1<arccos frac{3sqrt 2}5<arccos frac{sqrt 2}2,
0<arccosfrac{3sqrt2}{5}<frac{pi}{4}.
Отсюда fracpi 4+0<fracpi 4+arccos frac{3sqrt 2}5<fracpi 4+fracpi 4,
0<fracpi 4+arccos frac{3sqrt 2}5<fracpi 2,
0<a<fracpi 2.
Аналогично, -fracpi 4<arccosfrac{3sqrt2}{5}<0,
0=fracpi 4-fracpi 4<fracpi 4-arccos frac{3sqrt 2}5< fracpi 4<fracpi 2,
0<b<fracpi 2.
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac{3sqrt 2}5,, b-2pi =-frac74pi -arccos frac{3sqrt 2}5Bigg). При этом -2pi <a-2pi <-frac{3pi }2,
-2pi <b-2pi <-frac{3pi }2. Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac{3pi }2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac{7pi }2.
Ответ
а) fracpi4pm arccosfrac{3sqrt2}5+2pi k, kinmathbb Z;
б) -frac{7pi}4pm arccosfrac{3sqrt2}5.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Показать решение
Решение
а) Преобразуем уравнение:
cos x =-sin 2x,
cos x+2 sin x cos x=0,
cos x(1+2 sin x)=0,
cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
1+2 sin x=0,
sin x=-frac12,
x=(-1)^{k+1}cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^{k+1}cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1174
Условие
а) Решите уравнение frac{sin x-1}{1+cos 2x}=frac{sin x-1}{1+cos (pi +x)}.
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac{3pi }{2}; -frac{pi }2 right].
Показать решение
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1{1+cos 2x}=frac 1{1+cos (pi +x)}, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x, получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac{3pi }2 leqslant frac{pi }3+2pi m leqslant -frac pi 2 ,
2) -frac{3pi }2 leqslant -frac pi 3+2pi n leqslant -frac pi {2,}
3) -frac{3pi }2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
Решение:
1) -frac{3pi }2 leqslant frac{pi }3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac{11}6 leqslant 2m leqslant -frac56 , -frac{11}{12} leqslant m leqslant -frac5{12}.
Нет целых чисел, принадлежащих промежутку left [-frac{11}{12};-frac5{12}right].
2) -frac {3pi} 2 leqslant -frac{pi }3+2pi n leqslant -frac{pi }{2}, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1{6}, -frac7{12} leqslant n leqslant -frac1{12}.
Нет целых чисел, принадлежащих промежутку left[ -frac7{12} ; -frac1{12} right].
3) -frac{3pi }2 leqslant pi +2pi kleqslant -frac{pi }2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
б) -pi .
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1173
Условие
а) Решите уравнение: sin ^2x+sin ^2fracpi 6=cos ^22x+cos ^2fracpi 3.
б) Укажите все корни, принадлежащие промежутку left[ frac{7pi }2;,frac{9pi }2right).
Показать решение
Решение
а) Так как sin fracpi 6=cos fracpi 3, то sin ^2fracpi 6=cos ^2fracpi 3, значит, заданное уравнение равносильно уравнению sin ^2 x=cos ^2 2x, которое, в свою очередь, равносильно уравнению sin ^2- cos ^2 2x=0.
Но sin ^ 2x-cos ^2 2x= (sin x-cos 2x)cdot (sin x+cos 2x) и
cos 2x=1-2 sin ^2 x, поэтому уравнение примет вид
(sin x-(1-2 sin ^2 x)),cdot (sin x+(1-2 sin ^2 x))=0,
(2 sin ^2 x+sin x-1),cdot (2 sin ^2 x-sin x-1)=0.
Тогда либо 2 sin ^2 x+sin x-1=0, либо 2 sin ^2 x-sin x-1=0.
Решим первое уравнение как квадратное относительно sin x,
(sin x)_{1,2}=frac{-1 pm sqrt 9}4=frac{-1 pm 3}4. Поэтому либо sin x=-1, либо sin x=frac12. Если sin x=-1, то x=frac{3pi }2+ 2kpi , k in mathbb Z. Если sin x=frac12, то либо x=fracpi 6 +2spi , s in mathbb Z, либо x=frac{5pi }6+2tpi , t in mathbb Z.
Аналогично, решая второе уравнение, получаем либо sin x=1, либо sin x=-frac12. Тогда x =fracpi 2+2mpi , m in mathbb Z, либо x=frac{-pi }6 +2npi , n in mathbb Z, либо x=frac{-5pi }6+2ppi , p in mathbb Z.
Объединим полученные решения:
x=fracpi 2+mpi,minmathbb Z; x=pmfracpi 6+spi,s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток с помощью числовой окружности.
Получим: x_1 =frac{7pi }2, x_2 =frac{23pi }6, x_3 =frac{25pi }6.
Ответ
а) fracpi 2+ mpi , m in mathbb Z; pm fracpi 6 +spi , s in mathbb Z;
б) frac{7pi }2;,,frac{23pi }6;,,frac{25pi }6.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1172
Условие
а) Решите уравнение log_2^2(2sin x+1)-17log_2(2sin x+1) +16=0.
б) Укажите корни этого уравнения, принадлежащие отрезку left[ fracpi 4;,2pi right].
Показать решение
Решение
а) После замены t=log_2(2 sin x+1) исходное уравнение примет вид t^2 -17t+16=0. Корни этого уравнения t=1, t=16. Возвращаясь к переменной x, получим:
left[!!begin{array}{l} log_2(2 sin x+1)=1,\ log_2(2 sin x+1)=16; end{array}right. left[!!begin{array}{l} 2sin x+1=2,\ 2sin x+1=2^{16}. end{array}right.
Второе уравнение совокупности не имеет корней. Решая первое уравнение, получим:
sin x =frac12, x=(-1)^nfracpi 6+pi n,n in mathbb Z.
б) Запишем решение уравнения в виде x=fracpi 6 +2pi n,n in mathbb Z или x=frac{5pi }6+2pi k,kin mathbb Z и выясним, для каких целых значений n и k справедливы неравенства fracpi 4leqslant fracpi 6+2pi nleqslant 2pi и fracpi 4leqslant frac{5pi }6+2pi kleqslant 2pi.
Получим: frac1{24}leqslant nleqslant frac{11}{12} и -frac7{24}leqslant kleqslant frac7{12}, откуда следует, что нет целых значений n, удовлетворяющих неравенству frac1{24}leqslant nleqslant frac{11}{12};,,, k=0 — единственное целое k, удовлетворяющее неравенству -frac7{24}leqslant kleqslant frac7{12}.
При k=0, x=frac{5pi }6+2picdot 0=frac{5pi }6. Итак, frac{5pi }6 — корень уравнения, принадлежащий отрезку left[ fracpi 4;,2pi right].
Ответ
а) (-1)^nfracpi 6+pi n,n in mathbb Z.
б) frac{5pi }6.
Задание №1171
Условие
а) Решите уравнение 125^x-3cdot 25^x-5^{x+2}+75=0.
б) Укажите все корни этого уравнения, принадлежащие отрезку [log_54; log_511).
Показать решение
Решение
а) Преобразуем исходное уравнение и разложим на множители его левую часть.
5^{3x}-3cdot 5^{2x}-25cdot 5^x+25cdot 3=0,
5^{2x}(5^x-3)-25(5^x-3)=0,
(5^x-3)(5^{2x}-25)=0.
Получаем: 5^x-3=0 или 5^{2x}-25=0.
5^x-3=0, x=log_53 или 5^{2x}=25, x=1.
б) Нам нужно выбрать те корни уравнения, которые принадлежат отрезку [log_5 4; log_5 11]. Заметим, что log_5 3<log_5 4<1<log_5 11, значит, указанному отрезку принадлежит корень x=1.
Ответ
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1170
Условие
а) Решите уравнение 2cos xleft( cos x+cos frac{5pi }4right) + cos x+cos frac{3pi }4=0.
б) Найдите все корни этого уравнения, принадлежащие промежутку left[ pi ;,frac{5pi }2right).
Показать решение
Решение
а) Так как cos frac{5pi }4= cos left( pi +fracpi 4right) = -cos fracpi 4= -frac{sqrt 2}2 и cos frac{3pi }4= cos left( pi -fracpi 4right) = -cos fracpi 4= -frac{sqrt 2}2, то уравнение примет вид: 2cos xleft( cos x-frac{sqrt 2}2right) +cos x-frac{sqrt 2}2=0.Отсюда (2cos x+1)left( cos x-frac{sqrt 2}2right) =0.
Тогда cos x=-frac12; x=pmfrac{2pi }3+2pi n или cos x=frac{sqrt 2}2;, x=pmfracpi 4+2pi n, где n in mathbb Z.
б) Корни, принадлежащие промежутку left[ pi ;,frac{5pi }2right), найдём с помощью числовой окружности: frac{4pi }3;,, frac{7pi }4;,, frac{9pi }4.
Ответ
а) pmfrac{2pi }3+2pi n;,, pmfracpi 4=2pi n, n in mathbb Z.
б) frac{4pi }3;, frac{7pi }4;, frac{9pi }4.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
- Главная
- Учебники
- Алгебра, 11 класс
- ЕГЭ 2022, задание №12, уравнения тригонометрии с ограничениями
ЕГЭ 2022, задание №12, уравнения тригонометрии с ограничениями
Алгоритм: Решение уравнений с ограничениями: .
-
Надо выписать ОДЗ — условия: условия существования выражений в уравнении. Решить получившиеся неравенства.
-
На тригонометрической окружности Е.Т.О. отметить области, промежутки точек, выполняющих условия ОДЗ.
-
Решить уравнение, отметить точки на Е.Т.О. , соответствующие полученным сериям решений.
-
Выбрать те точки, которые «попали» в допустимые промежутки, области. Какие числа-углы соответствуют этим точкам?
-
Написать серии для этих точек — эти серии и будут корнями нашего уравнения.
-
Выписать несколько конкретных корней. Перебрать разные $n$, $m$ целые числа, игнорируя заведомо не попадающие в ограничения.
-
Проверить каждый кандидат — корень: удовлетворяет ли условиям ограничения, входит ли в требуемый промежуток?
Задача 1: а) Решите уравнение $left(sin^2frac{x}{2}+frac{3cdot cos x}{2}right)left(sqrt{3}ctg x+1right)sqrt{-7sin x}=0$ б) Укажите корни этого уравнения, принадлежащие отрезку $left[-4pi;-frac{pi}{2}right]$ .
- ОДЗ: под радикалом $-7sin xge0$ ; Условие на существование котангенса $xnepi n$ — тоже самое, что $sin xne0$;
- Итоговое ОДЗ: $sin x<0$ — корнями могуть быть углы из 3-ей и 4-ой четверти, в нижней части Е.Т.О окружности.
- Решаем уравнение: здесь произведение нескольких множителей равно 0. Значит, распад на случаи — каждый множитель = 0.
- Факт: «Произведение сравнить с нулем можно свести к сравнению с нулем каждого множителя»:
- Уравнение: $Acdot Bcdot C=0$ $Rightarrow$ I случай $A=0$ , II случай $B=0$ , III случай $C=0$
- Последнее $sqrt{-7sin x}=0$ незачем решать т.к. мы уже установили при ОДЗ, что $sin xne0$ из-за присутствия котангенса.
- I случай: $sin^2frac{x}{2}+frac{3cdot cos x}{2}=0$ .
- Какие здесь углы? $frac{x}{2}$ и $x$ . Значит, можем свести к одному углу!
- По формуле удвоенного угла $cos x=1-2sin^2frac{x}{2}$ сможем прийти к замене $y=sinfrac{x}{2}$. Но, решим по-другому …
- по формуле понижения степени — половинного угла: $frac{1-cos x}{2}+frac{3cdot cos x}{2}=0$ придем к простому
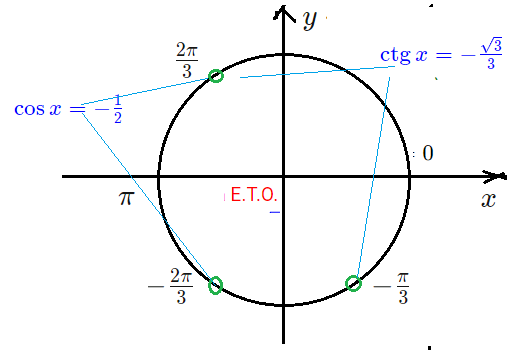
- $1+2cos x=0$ $Rightarrow$ $cos x=-frac{1}{2}$ его корни: $x=frac{2pi}{3}+2pi n$ $x=-frac{2pi}{3}+2pi m$
- Смотрим на Е.Т.О. — из этих двух точек-серий по ОДЗ нас устраивает только из 3-ей четверти: $x=-frac{2pi}{3}+2pi m$
- II случай: $sqrt{3}ctg x+1=0$ «если в уравнении лишь одна функция, ее следует выразить …»:
- $ctg x=-frac{sqrt{3}}{3}$ корни: 2 точки-серии $x=-frac{pi}{3}+pi k$. Устраивает по ОДЗ: $x=-frac{pi}{3}+2pi k$
- ответ a): $x=-frac{2pi}{3}+2pi m$ $x=-frac{pi}{3}+2pi k$ . (Две точки из нижней части Е.Т.О.).
- Пункт б): Ищем корни из требуемого промежутка $left[-4pi;-frac{pi}{2}right]$. Выпишем несколько возможных кандидатов для каждой серии:
- Из I серии: $-frac{2pi}{3}+2pi$, $-frac{2pi}{3}$, $-frac{2pi}{3}-2pi=-frac{8pi}{3}$, $-frac{2pi}{3}-4pi$. Входит: 2-ой и 3-ий.
- Из II серии: $-frac{pi}{3}+2pi$, $-frac{pi}{3}$, $-frac{pi}{3}-2pi=-frac{7pi}{3}$, $-frac{pi}{3}-4pi$. Попал лишь 3-ий.
- Требуемому ограничению удовлетворяют корни, ответ б): $-frac{2pi}{3}$, $-frac{7pi}{3}$, $-frac{8pi}{3}$,
Задача 2: а) Решите уравнение $frac{3cos^2 4x-7left(sin 4x+1right)}{sqrt{2sin x-1}}=0$ б) Укажите корни этого уравнения, принадлежащие отрезку $left[-4pi;frac{2pi}{3}right]$ .
- ОДЗ — условия: знаменатель не ноль, под радикалом неотрицательно: $2sin x-1>0$
- Надо понять какие точки удовлетворяют ОДЗ на тригонометрической окружности Е.Т.О. Реши неравенство.
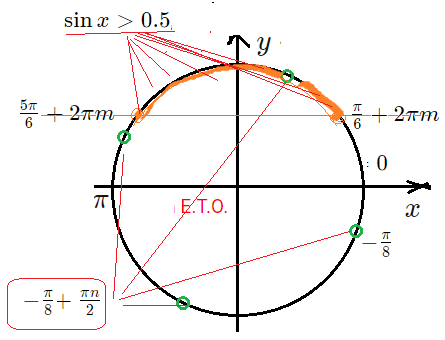
- Но пока уравнение: $2sin x-1=0$ $sin x=0.5$ $x=frac{pi}{6}+2pi m$ $x=frac{5pi}{6}+2pi m$
- Отметим эти точки-серии на Е.Т.О. Решение неравенства — это точки, в которых $sin x>0.5$ , значит точки с $y$ — координатой выше $>0.5$ .
- Значит, неравенство и ОДЗ выполняется в точках дуги , верхней части окружности между точками $frac{pi}{6}$ и $frac{5pi}{6}$.
- Теперь решаем само уравнение: «Дробь = 0 $Rightarrow$ числитель дроби = 0″. Алгоритм: $frac{A}{B}=0$ $Rightarrow$ $A=0$
- Итак: $3cos^24x-7left(sin4x+1right)=0$ У нас 2 функции, 1 аргумент. Выразим первую через вторую:
- $3cos^24x=1-sin^24x$ — Основное тождество, $3left(1-sin^24xright)-7left(sin4x+1right)=0$ .
- Упростим: $3sin^24x+7sin4x+4=0$ 1 функция, 1 аргумент — все готово к методу замены:
- замена $y=sin4x$ подстановка: $3y^2+7y+4=0$ корни: $y=-1$ $y=-frac{4}{3}$
- $y=-1$ возвратное: $sin4x=-1$ $Rightarrow$ $4x=-frac{pi}{2}+2pi n$ $Rightarrow$ $x=-frac{pi}{8}+frac{pi n}{2}$
- $y=-frac{4}{3}$ возвратное: $sin4x=-frac{4}{3}$ — нет решениий, т.к $-frac{4}{3}<-1$ , а синус не может стать меньше $<-1$
- Отметим серию $x=-frac{pi}{8}+frac{pi n}{2}$ — это точки, получающиеся от точки $-frac{pi}{8}$ прокруткой четверть оборотов $frac{pi}{2}$.
- Получаются четыре точки на Е.Т.О.: $-frac{pi}{8}$, $frac{3pi}{8}$, $7frac{pi}{8}$, $-5frac{pi}{8}$.
- Из этих 4-х точек в интервале ОДЗ $left(frac{pi}{6};frac{5pi}{6}right)$ находится только точка $frac{3pi}{8}$ .
- ОДЗ удволетворяют углы: $frac{3pi}{8}$ и его $2pi$ — прокуртки. ответ а): $frac{3pi}{8}+2pi n$
- Пункт б): Ищем корни из требуемого промежутка . Выпишем несколько возможных кандидатов из серии $frac{3pi}{8}+2pi n$:
- кандидаты: $frac{19pi}{8}$ $frac{3pi}{8}$ $-frac{13pi}{8}$ $-frac{29pi}{8}$ $-frac{45pi}{8}$ . Какие из них попадают в интервал $left[-4pi;frac{2pi}{3}right]$
- Проверка принадлежности промежутку ограничения: ответ б): $frac{3pi}{8}$ $-frac{13pi}{8}$ $-frac{29pi}{8}$,
Послесловие: Какие навыки, умения, смыслы, понятия надо знать?
- Е.Т.О — связь углов, точек на окружности, серии углов, прокрутки в пол-оборота, полный оборот, части.
- Формулы решения простейших тригонометрических уравнений, интерпретация в виде точек на Е.Т.О.
- Решение неравенств, изображение решений на Е.Т.О. Перевод точек на серии углов и наоборот.
- Анализ ОДЗ: радикалы, знаменатели, тангенс-котангенс. Анализ условий ограничений. Интерпретация на Е.Т.О.
- Методы решения тригонометрических уравнений: простейших, метод замены, разложение на множители, понижение степени, однородные.
Интерактивная Доска
Упражнения
Наверх

Задание №1 ЕГЭ 2022 профильный уровень тригонометрические уравнения 6 задач решу ЕГЭ с ответами и решением для подготовки, решаем примеры и готовимся к ЕГЭ.
Скачать файл заданий с ответами
Тригонометрические уравнения задания реши ЕГЭ 2022 профиль:
1)Решите уравнение cos pi(x-7)/3=1/2. В ответе запишите наибольший отрицательный корень.
Ответ: -4
2)Решите уравнение tg pi(x+2)/3=-корень из 3. В ответе запишите наибольший отрицательный корень.
Ответ: -3
3)Решите уравнение sin pi(2x-3)/6=-0,5. В ответе запишите наибольший отрицательный корень.
Ответ: -1
4)Решите уравнение cos pi(8x+1)/6=корень из 3/2. В ответе запишите наименьший положительный корень.
Ответ: 1,25
5)Решите уравнение tg pi(x-5)/3=-корень из 3. В ответе запишите наименьший положительный корень.
Ответ: 1
6)Решите уравнение sin pix/3=0,5. В ответе запишите наименьший положительный корень.
Ответ: 0,5
Другие тренировочные варианты ЕГЭ 2022 по математике 11 класс
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
- ЕГЭ по математике профиль
Прототипы задания №12 ЕГЭ по математике профильного уровня — уравнения. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №12 необходимо уметь решать уравнения и неравенства.
Практика
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Максимальный балл за выполнение задания — 2
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 10
Связанные страницы:






.png)



