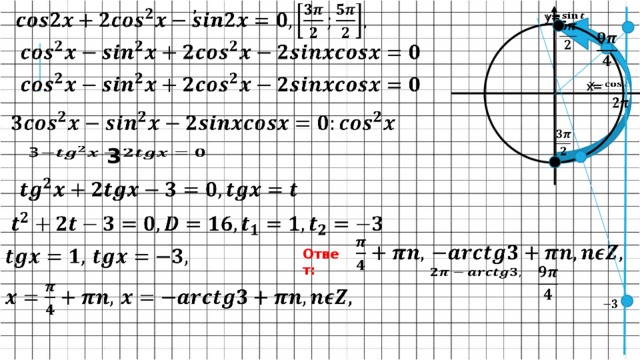Слайд 1
Решение тригонометрических уравнений С1 Балагурова-Шемота Н.Ю лицей №90
Слайд 2
До экзамена осталось 160 дней лицей №90 Балагурова-Шемота Н.Ю. 2
Слайд 3
Повторим лицей №90 Балагурова-Шемота Н.Ю. 3
Слайд 4
Повторим лицей №90 Балагурова-Шемота Н.Ю. 4
Слайд 5
лицей №90 Балагурова-Шемота Н.Ю. 5
Слайд 6
лицей №90 Балагурова-Шемота Н.Ю. 6 sin α = №0 Мизинец 0 0 №1 Безымянный 30 0 №2 Средний 45 0 №3 Указательный 60 0 №4 Большой 90 0
Слайд 7
лицей №90 Балагурова-Шемота Н.Ю. 7
Слайд 8
лицей №90 Балагурова-Шемота Н.Ю. 8
Слайд 9
Отбор корней лицей №90 Балагурова-Шемота Н.Ю. 9
Слайд 10
Найти ошибку лицей №90 Балагурова-Шемота Н.Ю. 10
Слайд 11
лицей №90 Балагурова-Шемота Н.Ю. 11
Слайд 12
лицей №90 Балагурова-Шемота Н.Ю. 12
Слайд 13
лицей №90 Балагурова-Шемота Н.Ю. 13
Слайд 14
Ответ: лицей №90 Балагурова-Шемота Н.Ю. 14
Слайд 15
лицей №90 Балагурова-Шемота Н.Ю. 15
Слайд 16
лицей №90 Балагурова-Шемота Н.Ю. 16
Слайд 17
лицей №90 Балагурова-Шемота Н.Ю. 17 , и .
Слайд 18
Ответ: лицей №90 Балагурова-Шемота Н.Ю. 18
Слайд 19
лицей №90 Балагурова-Шемота Н.Ю. 19
Слайд 20
лицей №90 Балагурова-Шемота Н.Ю. 20
Слайд 21
лицей №90 Балагурова-Шемота Н.Ю. 21
Слайд 22
НАЙТИ ОШИБКУ лицей №90 Балагурова-Шемота Н.Ю. 22
Слайд 23
http://mathege.ru/or/ege/Main Открытый банк заданий http://uztest.ru/exam?idexam=30 http :// egeurok . ru / generators / ege _ matem _2014/ generator _ variantov _ ege _ matem _2014. html Генератор вариантов http://alexlarin.net/ege14.html Ларин Александр Александрович http://reshuege.ru/ лицей №90 Балагурова-Шемота Н.Ю. 23
Слайд 24
Повтори лицей №90 Балагурова-Шемота Н.Ю. 24
1.
Ох уж, эта
тригонометрия!
(Подготовка к ЕГЭ
по математике)
2.
Полезные советы при решении части 1
1
Прочитайте условие задачи. Если уверены, что умеете решать её – делайте
это сразу, если же есть сомнение, то переходите к следующей.
2
Решайте задачу не торопясь – обидно получить 0 баллов по
невнимательности или из-за описки.
3
Особое внимание уделите проверке выполнения арифметических
действий.
4
Если после второго прохода остались «белые пятна», не заполняйте их
«наугад». Постарайтесь вернуться к ним в конце всей работы.
5
Если вам кажется, что вопрос слишком прост, не ищите подвоха –
части 1 есть действительно простые вопросы.
6
В задачах части 1 полученный ответ часто можно проверить, подставив его
в исходную задачу, – сделайте это, если такая возможность есть.
7
На экзамене отсутствует справочный материал, поэтому постарайтесь
вспомнить (вывести) необходимые формулы и т.д.
в
3.
Полезные советы при решении части 2
1
После выполнения заданий части 1 сделайте небольшой перерыв,
отвлекитесь, а затем снова настройтесь на спокойную и вдумчивую работу.
2
Приготовьтесь к тому, что задачи этой части имеют «подводные камни».
3
Не забывайте о краткости записи решения при «полном» обосновании.
4.
Тригонометрия
5.
В чём ошибка?
cos x = 0,2, x = arccos 0,2 + 2Пn,
sin x = 0,2, x = (-1)ᵏarcsin 0,2 + Пn.
!!!
6.
!
!!
По мнению многих учеников, запись «n € Z» — избыточная.
В записи с использованием символа «±» теряется идея двух
серий решений тригонометрического уравнения.
7.
!!!
В формуле корней простейшего тригонометрического
уравнения sin t = a теряются идеи как двух серий решений
тригонометрического уравнения, так и периодичность
функции синус.
8.
Учимся решать!
9.
Тригонометрия на ЕГЭ
Решите уравнение
Задания В5
.
В ответе напишите наибольший отрицательный корень.
10.
Тригонометрия на ЕГЭ
Найдите значение выражения
Задания В7
.
11.
Тригонометрия на ЕГЭ
Найдите
Задания В7
12.
Тригонометрия на ЕГЭ
Задания В12
Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по
закону
, где t — время в секундах. Кинетическая энергия
груза, измеряемая в джоулях, вычисляется по формуле
,
где m — масса груза (в кг), v — скорость груза (в м/с). Определите, какую
долю времени из первой секунды после начала движения кинетическая
энергия груза будет не менее
Дж. Ответ выразите десятичной
дробью, если нужно, округлите до сотых.
13.
14.
Тригонометрия на ЕГЭ
Найдите точку минимума функции
,
принадлежащую промежутку
у’
у
.
0
Задания В14
—
0,5
+
15.
Тригонометрия на ЕГЭ
Найдите наибольшее значение функции
на отрезке
.
Задания В14
16.
Ура тестам!
17.
Найдите область определения выражения
При каких значениях х
имеет смысл выражения
.
.
18.
Укажите в каких
четвертях расположен ctg x , если
1и4
1и3
1и2
.
2и4
Укажите какие значения может принимать sin x ,
если у² = 4 sin x.
sin x > 0
sin x < 0
sin x 0
sin x 0
19.
Укажите какие значения может принимать tg x ,
если
.
tg x > 0
tg x < 0
tg x 0
tg x 0
Укажите в каких четвертях расположен cos x , если
3ʸ + 2cos x = 0.
1и4
1и2
2и3
3и4
20.
Хочу всё знать!
Задание С1
21.
Решить уравнение:
22.
Решите уравнение:
23.
Решите уравнение:
24.
25.
Чем мы хуже
МИОО?
26.
При каких значениях р имеет решения
уравнение 2 sin 2 x 2 p cos x 6 p 7 cos x 5
sin x 1
0.
Решение :
sin x 1 0, sin x 1, значит, sin x 1, cos х 0.
2 cos 2 x (2 p 7) cos x (6 p 3) 0,
cos x t , 1 t 1, 2t 2 ( 2 p 7)t (6 p 3) 0,
D (2 p 5) 2 0 при p R,
t1 p 0,5, t 2 3 не удовлетворяет 1 t 1.
1 p 0,5 1, 1,5 р 0,5,
Значит,
p 0,5 0;
р 0,5.
Ответ : р 1,5; 0,5) ( 0,5; 0, 5 .
27.
Всемирная паутина
на службе у ЕГЭ!
28.
http://avangard-school.nm.ru/
http://www.ctege.org/content/category/15/67/48/
http://rsr-olymp.ru/splash/
http://www.alleng.ru/edu/phys1.htm
http://alexlarin.narod.ru/ege.html
http://ege.stavedu.ru/
http://mathgia.ru:8080/or/gia12/
http://mathege.ru/or/ege/Main
http://shpargalkaege.ru/
http://pedsovet.su/
http://ege.do.am/news/shpargalka_dlja_ekzamena/2010-12-18-160
http://pedsovet.org/
http://www.openclass.ru/
http://1september.ru/
http://festival.1september.ru/
http://edu.1september.ru/
http://portfolio.1september.ru/
http://www.mcppomsk.ru/index.php?option=com_content&view=article&i
d=1&Itemid=1
http://le-savchen.ucoz.ru/
29.
Какое из данных уравнений не имеет
решений?
1) cos (2x – π) =
5
3
3) ctg x = 3;
Ответ: 4.
; 2) sin 0,3x
3
= 3 ;
10
4) 2sin x· cos x =
.
3
30.
Решите уравнение:
2 sin² x – sin x – 1 = 0.
2
2 n, n ; ( 1)
k
6
k , k
31.
Кот в мешке
Выберите среди данных уравнений однородное
уравнение первой степени и решите его:
1) сos x – sin 3x = 0;
2) cos x – 3sin x = 0;
3) cos x – 3sin x = 2;
4) cos² x – 3sin x = 0.
cos x – 3sin x = 0
32.
Решите уравнение:
4sin² x + 5 sin x cos x + cos² x = 0.
1
x n, n ; x arctg k , k
4
4
33.
Даны неравенства:
cos x >0, sin x 0,
sin x -0,5.
Укажите какое-либо число, удовлетворяющее
всем трём неравенствам одновременно.
34.
Решите уравнение sin 2x – 3 cos x = 0.
2 sin x cos x 3 cos x 0,
cos x (2 sin x 3) 0,
cos x 0
x
2
или
n, n
2 sin x 3 0,
sin x 1,5 решений нет.
Ответ :
2
n, n .
35.
Найдите наименьший корень уравнения
2cos² x = 1 + sin x.
2(1 sin 2 x) 1 sin x,
2 sin 2 x sin x 1 0,
sin x 1
1
sin x ,
2
или
Наименьший положительный корень х .
6
36. При каких значениях х значения функции равно 0?
При каких значениях х значения функции
x
x
f ( x) 4 sin cos 1
2
2
равно 0?
x
x
1
4 sin cos 1 0, 2 sin x 1, sin x ,
2
2
2
x ( 1)
k
6
k , k
37.
Выберите уравнение, которое имеет решение,
показанное на единичной окружности:
1) tg x = 1;
2) sin x = 0;
1
3) сos x = 2 ;
3
4) sin x =
.
2
38.
Вопрос от учителя
Какая ошибка допущена в решении уравнения?
tg ( 2 x
2x
2x
x
4
3
24
4
) 3,
arctg 3 n, n ,
4
n, n ,
2 n, n .
39.
Аукцион
Укажите на тригонометрической окружности все точки,
удовлетворяющие неравенству: sin x > 0,5.
40.
Какой корень уравнения
х
cos = 1 принадлежит отрезку [ -π; π]?
2
х=0
41.
При каких значениях а уравнение
sin² x – (a + 3) sin x + 3a = 0
не имеет решений?
2
Пусть sin x t , t 1. t (a 3) t 3a 0.
D (a 3) 0 при а R, t1 3, t 2 a.
2
Значит, уравнение не будет иметь корней
при а ( ; 1) (1; ).
42.
Кот в мешке
Найдите значения х, при которых график функции
у 2 cos х 1 лежит выше оси х.
2 cos х 1 0, cos x
1
2
,
4
2 n x
4
2 n, n
43.
Как, не решая уравнения ctg 2 x 1
1
sin 2 x
,
определить, какая серия является решением?
1)
2
n, n
3) n, n
1)
2) 2 n, n
4)
n
2
, n
44.
Найдите все х, обращающие в нуль произведение
2
функций у cos x
2
и
у sin 4 x .
2
cos x
sin 4 x 0,
2
cos x
2
2
или
sin 4 x 0
4 x n, n
x
n
4
, n
45.
Вопрос от учителя
Решите неоднородное уравнение второй степени
2sin² x – 5 sin x cos x + 5 cos² x = 1.
2 sin 2 x 5 sin x cos x 5 cos 2 x sin 2 x cos 2 x,
sin 2 x 5 sin x cos x 4 cos 2 x 0, разделим на cos 2 x,
tg 2 x 5 tg x 4 0,
tg x 1
x
4
n, n
или
tg x 4
x arctg 4 m, m
46.
Решите уравнение sin² x + cos 2x = b, если
одно из его решений
6
.
2 1 1 3
b sin
cos
.
6
6 4 2 4
3 1 cos 2 x
3
2
sin x cos 2 x ,
cos 2 x ,
4
2
4
2
2 2 cos 2 x 4 cos 2 x 3,
2x
3
2 n, n , x
6
1
2 cos 2 x 1, cos 2 x ,
2
n, n
47.
Решите уравнение cos x + sin x = cos 3x.
(cos 3 x cos x) sin x 0,
2 sin 2 x sin x sin x 0,
sin x ( 2 sin 2 x 1) 0,
sin x 0
x n, n
или
1
sin 2 x
2
2 x ( 1)
x ( 1)
k 1
k 1
6
12
k , k ,
k
2
, k
48.
Решите уравнение
2 sin x 2 0,
2 cos 2 0;
2 sin x 2
2 cos 2
sin x
cos x
x 2 n, n
4
2
,
2
2
2
0 .
49.
СУПЕРИГРА
Решите уравнение 1 tg x x
2
1 tg 2 x x 2 4 x 2 ,
2 x 2
2
3
n 2
6
6
n
3
3
n 0, x
3
2
tg 2 x 3,
2 x 2
2
3
4 x
x
n, n ,
3
2 x 2
n 2
6
6
n
3
3
n 0, x
2
3
2
.
50. М о л о д ц ы ! ! !
Молодцы!!!
1
Подготовка школьников к ЕГЭ: особенности решения тригонометрических уравнений Кафедра математического образования 2015
2
План 1)Методические особенности работы с числовой окружностью. 2)Методика обучения решению простейших тригонометрических уравнений. 3)Организация учебной деятельности школьников по освоению способов решения тригонометрических уравнений с выбором корней: с использованием числовой окружности; без числовой окружности 4)Методические особенности решения более сложных тригонометрических уравнений. 5)Фрагменты коллекции тригонометрических уравнений для подготовки к ЕГЭ по математике. 6)Перечень полезных информационных ресурсов для учителя в освоении способов обучения решению тригонометрических уравнений.
3
В 10 классе у учащихся необходимо сформировать знания и умения отмечать на числовой окружности точки, соответствующие числам:
4
1) Задания на вычисление длины дуги единичной окружности.
5
2) Задания на отыскание на числовой окружности точек, соответствующих заданным числам.
6
3) Задания на запись чисел, соответствующих данной точке числовой окружности.
7
4) Задания на составление аналитических записей для дуг числовой окружности.
8
5) Задание на изображение промежутков, заданных аналитической записью.
9
2π2π4π4π π 2 π 2 На числовой оси:
10
6) Задания на сравнение. а) Сравните и, и.
11
б) Расположите в порядке возрастания:
12
7) Задания на объединение чисел. 1. Объединить и записать числа
13
14
15
16
2. Объединить числа
17
18
19
На первых уроках обучения решению тригонометрических уравнений необходимо включать в содержание задачи, которые : 1) формируют у учащихся понимание особенностей записи корней в виде числовых серий, 2) позволяют формировать устойчивые навыки работы с этими числовыми сериями. Примером такого набора заданий могут быть следующие:
20
Решите уравнения:
21
10
22
0
23
0
24
0
25
0 Х
26
1 0
27
В А 0
28
или 0 Х
29
0 Х Второй способ.
30
Домашнее задание Решите уравнения:
31
Ответы к домашнему заданию:
32
Решите уравнения:
33
Решение уравнений с выбором ответа на числовой окружности 1) Х Х 0
34
2)Найдите все корни уравнения, удовлетворяющие условию Решим полученные уравнения с учетом условия, используя числовую окружность. Ось тангенсов Х 0
35
3) Х Х 0
36
4) Х Х 0
37
5) 0
38
6) Х Х 0
39
Решение предложенных далее уравнений поможет учащимся в совершенствовании способов решения тригонометрических уравнений, сводящихся к простейшим с выбором корней без числовой окружности.
40
Решение или Ответ : 1)1)
41
2) Решение или Ответ :
42
3) Решение
43
4) 5)
44
6) 7) 
45
9)
46
Оценивание задания (ЕГЭ 2015)
47
1. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение
48
С учетом условия решим полученные простейшие уравнения с использованием числовой окружности. 0 Х Решим уравнение системы.
49
Способ перебора.
50
Составление и решение неравенства.
51
C помощью числовой окружности. 0 Ответ: 0 Х Х
52
2. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение (1 способ) а)
53
Решение уравнения (2 способ)
54
Ось тангенсов 0
55
Составление и решение неравенств.
56
С помощью числовой окружности. Ответ: Х
57
3. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение
58
0 Ось тангенсов Х
59
Составление и решение неравенств.
60
С помощью числовой окружности. Ответ: 0 Ось тангенсов Х
61
4. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение
62
0 Ось тангенсов
63
С помощью составления и решения неравенств выберем корни, принадлежащие промежутку
64
С помощью числовой окружности. Ответ: 0 Ось тангенсов
65
5. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение
66
Решение системы. С учетом условия : х=3.
67
Решение уравнения.
68
С помощью составления и решения неравенства выберем корни, входящие в промежуток. Ответ:
69
Перебором определим корни, входящие в промежуток. Ответ:
70
Информационные ресурсы 1)ЕГЭ. Математика задач. Профильный уровень. Закрытый сегмент / Ященко И. В., Захаров П. И., Высоцкий И. Р.; под ред. Лаппо Л. Д. — Издательство: Экзамен, )ЕГЭ. Математика задач с ответами. Базовый и профильный уровни / Высоцкий И. Р., Ященко И. В., Забелин А. В. — Издательство: Экзамен, )Математика. Решение заданий повышенного и высокого уровня сложности. Как получить максимальный балл / Семенов А. В., Ященко И. В., Трепалин А. С. — Издательство: Интеллект-Центр, 2015.
71
4) – сайт Александра Ларина. 5)reshuege.ru – сайт Дмитрия Гущина.reshuege.ru 6)egeigia.ru – информационный портал в помощь подготовки к ЕГЭ и ОГЭ.egeigia.ru 7)mathege.ru – открытый банк заданий.mathege.ru 8)webmath.exponenta.ru – сайт, включающий методы решения тригонометрических уравнений.webmath.exponenta.ru 9)uztest.ru – сайт, содержащий теоретические сведения о решении тригонометрических уравнений и on-line тесты.uztest.ru 10)nsportal.ru – информационный портал, содержащий методические наработки разных учителей математики (Социальная сеть работников образования ).nsportal.ru
Данная презентация составлена из типовых заданий по матаматике под редакцией Ященко И.В.,.20117г. Анимация позволяет подробно объяснить решение и выбор корней на отрезке, вращаясь по окружности.
Вы уже знаете о суперспособностях современного учителя?
Тратить минимум сил на подготовку и проведение уроков.
Быстро и объективно проверять знания учащихся.
Сделать изучение нового материала максимально понятным.
Избавить себя от подбора заданий и их проверки после уроков.
Наладить дисциплину на своих уроках.
Получить возможность работать творчески.
Просмотр содержимого документа
«Тригонометрические уравнения для подготовки к ЕГЭ»
—
—
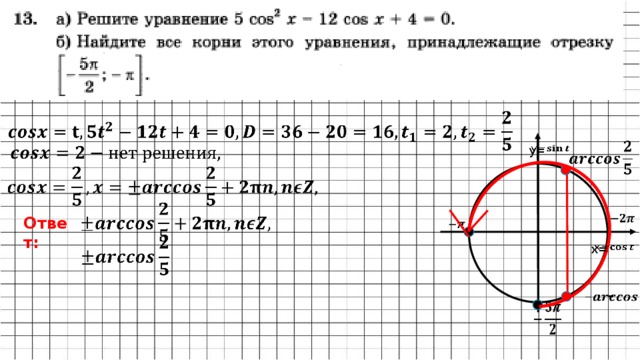
Решение
-5t-4=0,D=25+96=121,= ,==-
—
y=
ет решения,
—
Ответ :
,
—
x=
—
— ,
-1/2
—
—
—
—
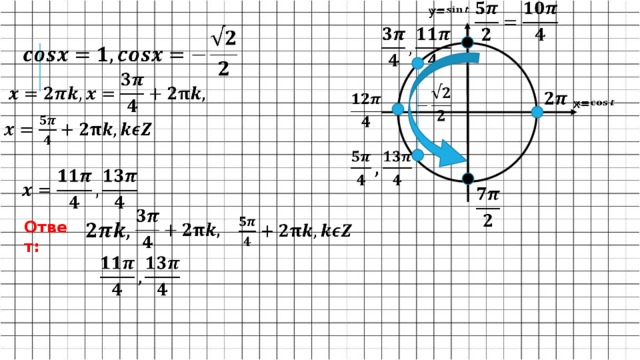
y=
x=
Ответ:
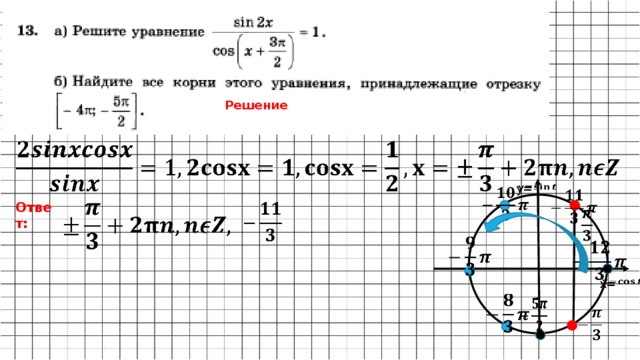
= 1,
y=
x=
Ответ:
0, ±
Решение
y=
Ответ:
x=
y=
Ответ:
x=
—
6
6 = 1,
y=
Ответ:
x=
,
,
y=
x=
Ответ:
2
y=
x=
Ответ:
y=
x=
Ответ:
y=
x=
Ответ:
y=
x=
-1
Ответ :
y=
—
x=
—
Ответ :
y=
x=
—
Ответ :
,
y=
x=
3
Ответ :
y=
x=
Ответ:
,
Ответ:
,
,
,
,
y=
x=
3
Ответ:
В презентации разобраны решения сложных примеров из ЕГЭ профильного уровня.
Триг. урав. профил. ЕГЭ.pptx
Тригонометрические уравнения профильного уровня
Тригонометрические уравнения профильного уровня ЕГЭ.Задание №12.
Школа №12
г. Северодвинск.
Шкода Л.И.
Презентация «Тригонометрические уравнения профильного уровня из материалов ЕГЭ».
Пример 2.
Пример 2.
Пример 3.
Пример 3.
Пример 4.
Пример 4.
Пример 5 .
Пример 5 .
Пример 6.
Пример 6.
Пример 7.
Пример 7.
Пример 8.
Пример 8.
Пример 9.
Пример 9.
Пример 10.
Пример 10.
Пример 11.
Пример 11.
Пример 12.
Пример 12.
Пример 13.
Пример 13.
Пример 14.
Пример 14.
ПРИМЕР 15.
ПРИМЕР 15.
Пример 16.
Пример 16.
Примеры для самостоятельного решения
1
Примеры для самостоятельного решения.
Презентация «Тригонометрические уравнения профильного уровня из материалов ЕГЭ».
Презентация «Тригонометрические уравнения профильного уровня из материалов ЕГЭ».
Материалы на данной страницы взяты из открытых истончиков либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.
Введите ваш emailВаш email
Решение тригонометрических уравнений и неравенств(подготовка к ЕГЭ)
презентация к уроку по алгебре (11 класс) по теме
Рассмотрены способы решения тригонометрических уравнений и неравенств
Скачать:
| Вложение | Размер |
|---|---|
| Решение тригонометрических уравнений и неравенств | 1.43 МБ |
| reshenie_trigonometricheskih_uravneniy_-2.ppt | 1.68 МБ |
Предварительный просмотр:
Подписи к слайдам:
Предварительный просмотр:
Подписи к слайдам:
МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
№ Уравнения № метода Методы 1 Sin x/3 — cos 6x = 2 4(б) 1.Разложение на множители. 2.Введение новой переменной: а) сведение к квадратному; б) универсальная подстановка; в) введение вспомогательного аргумента. 3. Сведение к однородному уравнению. 4. Использование свойств функций, входящих в уравнение: а) обращение к условию равенства тригонометрических функций; б) использование свойства ограниченности функции. 2 3 4 5 sinx – 2 cosx = 1 3, 2(б,в) 5 sin3x cos2x = 1 4(б) 6 cos2x = (cos x – sin x ) 1,2(б,в),3 7 1 – sin2x = cos x – sin x 1,2(б,в)3 8 cos3x = sin x 4(а) 9 4 – cos 2 x = 4 sin x 2(а) 10 sin3x – sin5x = 0 4(б) 11 tg 3x tg(5x + /3) = 1 4(а) 12 2 tg x/2 — cos x = 2 1,2(а,б,в),3,4(а)
1. Какие методы решения тригонометрических уравнений вы знаете? 2. Определите и ответьте, какими методами нужно решать данные тригонометрические уравнения? а ) sin 2x – cos x = 0 б ) 2sin²x — 5sinx = -3 в ) cos²x – sin²x = sinx – cosx г ) sin2 x – 3sinx cosx + 2cos²x = 0 3. Решите простейшие тригонометрические уравнения:
Некоторые типы тригонометрических уравнений . Уравнения, сводящиеся к квадратным, относительно cos х = t , sin х = t . A sin 2 x + B cosx + C = 0 A cos 2 x + В sinx + C = 0 Решаются методом введения новой переменной. 2.Однородные уравнения первой и второй степени. I степени . A sinx + B cosx = 0 : cosx A tg x + B = 0 II степени . A sin 2 x + B sinx cosx + A cos 2 x = 0 : cos 2 x A tg 2 x + B tgx + C = 0 Решаются методом разложения на множители и методом введения новой переменной . 3. Уравнение вида: А sinx + B cosx = C . А, В, С 0 Применимы все методы.
4. Понижение степени. А cos 2 x + В = C . A cos2x + B = C. Решаются методом разложения на множители. A sin2x + B = C. A sin2x + B = C. Сводятся к однородным уравнениям С = С( ).
Формулы . a cosx + b sinx заменим на C sin ( x + ), где sin = cos = — вспомогательный аргумент. Универсальная подстановка. х + 2 n ; Проверка обязательна! Понижение степени. = (1 + cos2x ) : 2 = (1 – cos 2x) : 2 Метод вспомогательного аргумента.
Сведение к однородному. sinx cosx + 6 cos 2 x = 5. Пример. 5 sin 2 x + Разложение на множители. Пример. — 2 cosx = 4 sinx — sin 2 x A sin2x + B sin 2 x = C, Asin2x + Bcos 2 x = C. Уравнения вида
1.Потеря корней: делим на g (х). опасные формулы (универсальная подстановка). Этими операциями мы сужаем область определения. 2. Лишние корни: возводим в четную степень. умножаем на g (х) (избавляемся от знаменателя). Этими операциями мы расширяем область определения. Проблемы ,возникающие при решении тригонометрических уравнений
Уравнение . Уравнение . Поделив уравнение на , получим , , При решении этой задачи обе части уравнения были поделены на . Напомним, что при делении уравнения на выражение, содержащее неизвестное, могут быть потеряны корни. Поэтому нужно проверить, не являются ли корни уравнения корнями данного уравнения. Если , то из уравнения следует, что . Однако и не могут одновременно равняться нулю, так как они связаны равенством . Следовательно, при делении уравнения , где , , на (или ) получаем уравнение, равносильное данному.
, x = y + . Решить уравнение cos²x + sinx cosx = 0 1) Делить на cosx нельзя, так как в условии не указано , что cosx не равен нулю. Но можно утверждать, что sinx не равен нулю, так как в противном случае cosx равен 0, что невозможно , так как sin²x-cos²x =1. Значит можно разделить на sin²x . 2) Решим уравнение разложением на множители: cos²x + sinx cosx = 0 , с osx ( cosx + sinx ) = 0 , с osx = 0 или cosx + sinx = 0, tg x=-1,
Уравнения, линейные относительно sin x и cos x а sin x + в cos x = с. Если а=в=0, а с не равно 0, то уравнение теряет смысл; Если а=в=с=0, то х – любое действительное число, то есть уравнение обращается в тождество. Рассмотрим случаи, когда а , в , с не равны 0. Примеры: 3 sin 5x — 4 cos 5x = 2 2 sin 3x + 5 cos 3x = 8. Последнее уравнение не имеет решений, так как левая часть его не превосходит 7. Уравнения, этого вида можно решить многими способами: с помощью универсальной подстановки, выразив sin x и cos x через tg х ; сведением уравнения к однородному; введением вспомогательного аргумента и другими. Решение этих уравнений существует при
Данное уравнение является уравнением вида , (1) где , , , которое можно решить другим способом. Разделим обе части этого уравнения на : . (2) Введем вспомогательный аргумент , такой, что . Такое число существует, так как . Таким образом, уравнение можно записать в виде . Последнее уравнение является простейшим тригонометрическим уравнением.
Уравнение . Используя формулы sin x = 2 sin cos , cos x = cos 2 — sin 2 и записывая правую часть уравнения в виде , получаем Поделив это уравнение на , получим равносильное уравнение Обозначая , получаем , откуда . 1) 2) Ответ: . 0 2 cos 2 cos 2 sin 4 2 sin 3 2 2 x x x x
4 sin ²x – 4sinx – 3 = 0 2cos²x – sinx – 1 = 0
4 sin ²x — 4 sinx – 3 = 0 ( -1) n+1 П /6 + П n, n Z. 2 с os²x – sin x – 1 = 0 ± П /6 + П n ; -П /2+2 П n, n Z.
Решить уравнение Здесь Поделим обе части уравнения на 5: Введем вспомогательный аргумент , такой, что , . Исходное уравнение можно записать в виде , , откуда Ответ:
1 ctg x 1 tg x cos x sin x = 60 ° =45 ° =30 °
— 0 — 0 — ctg x 0 — 0 — 0 tg x 1 0 -1 0 1 cos x 0 -1 0 1 0 sin x =360 ° =270 ° =180 ° = 90 ° 0 ° А
Подготовка школьников к ЕГЭ: особенности решения тригонометрических уравнений Кафедра математического образования 2015. — презентация
Презентация была опубликована 6 лет назад пользователемСнежана Пущина
Похожие презентации
Презентация по предмету «Математика» на тему: «Подготовка школьников к ЕГЭ: особенности решения тригонометрических уравнений Кафедра математического образования 2015.». Скачать бесплатно и без регистрации. — Транскрипт:
1 Подготовка школьников к ЕГЭ: особенности решения тригонометрических уравнений Кафедра математического образования 2015
2 План 1)Методические особенности работы с числовой окружностью. 2)Методика обучения решению простейших тригонометрических уравнений. 3)Организация учебной деятельности школьников по освоению способов решения тригонометрических уравнений с выбором корней: с использованием числовой окружности; без числовой окружности 4)Методические особенности решения более сложных тригонометрических уравнений. 5)Фрагменты коллекции тригонометрических уравнений для подготовки к ЕГЭ по математике. 6)Перечень полезных информационных ресурсов для учителя в освоении способов обучения решению тригонометрических уравнений.
3 В 10 классе у учащихся необходимо сформировать знания и умения отмечать на числовой окружности точки, соответствующие числам:
4 1) Задания на вычисление длины дуги единичной окружности.
5 2) Задания на отыскание на числовой окружности точек, соответствующих заданным числам.
6 3) Задания на запись чисел, соответствующих данной точке числовой окружности.
7 4) Задания на составление аналитических записей для дуг числовой окружности.
8 5) Задание на изображение промежутков, заданных аналитической записью.
9 2π2π4π4π π 2 π 2 На числовой оси:
10 6) Задания на сравнение. а) Сравните и, и.
11 б) Расположите в порядке возрастания:
12 7) Задания на объединение чисел. 1. Объединить и записать числа
16 2. Объединить числа
19 На первых уроках обучения решению тригонометрических уравнений необходимо включать в содержание задачи, которые : 1) формируют у учащихся понимание особенностей записи корней в виде числовых серий, 2) позволяют формировать устойчивые навыки работы с этими числовыми сериями. Примером такого набора заданий могут быть следующие:
29 0 Х Второй способ.
30 Домашнее задание Решите уравнения:
31 Ответы к домашнему заданию:
33 Решение уравнений с выбором ответа на числовой окружности 1) Х Х 0
34 2)Найдите все корни уравнения, удовлетворяющие условию Решим полученные уравнения с учетом условия, используя числовую окружность. Ось тангенсов Х 0
39 Решение предложенных далее уравнений поможет учащимся в совершенствовании способов решения тригонометрических уравнений, сводящихся к простейшим с выбором корней без числовой окружности.
40 Решение или Ответ : 1)1)
41 2) Решение или Ответ :
46 Оценивание задания (ЕГЭ 2015)
47 1. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение
48 С учетом условия решим полученные простейшие уравнения с использованием числовой окружности. 0 Х Решим уравнение системы.
50 Составление и решение неравенства.
51 C помощью числовой окружности. 0 Ответ: 0 Х Х
52 2. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение (1 способ) а)
53 Решение уравнения (2 способ)
54 Ось тангенсов 0
55 Составление и решение неравенств.
56 С помощью числовой окружности. Ответ: Х
57 3. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение
58 0 Ось тангенсов Х
59 Составление и решение неравенств.
60 С помощью числовой окружности. Ответ: 0 Ось тангенсов Х
61 4. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение
62 0 Ось тангенсов
63 С помощью составления и решения неравенств выберем корни, принадлежащие промежутку
64 С помощью числовой окружности. Ответ: 0 Ось тангенсов
65 5. а) Решите уравнение б) Найдите все корни этого уравнения, принадлежащие промежутку. Решение
66 Решение системы. С учетом условия : х=3.
68 С помощью составления и решения неравенства выберем корни, входящие в промежуток. Ответ:
69 Перебором определим корни, входящие в промежуток. Ответ:
70 Информационные ресурсы 1)ЕГЭ. Математика задач. Профильный уровень. Закрытый сегмент / Ященко И. В., Захаров П. И., Высоцкий И. Р.; под ред. Лаппо Л. Д. — Издательство: Экзамен, )ЕГЭ. Математика задач с ответами. Базовый и профильный уровни / Высоцкий И. Р., Ященко И. В., Забелин А. В. — Издательство: Экзамен, )Математика. Решение заданий повышенного и высокого уровня сложности. Как получить максимальный балл / Семенов А. В., Ященко И. В., Трепалин А. С. — Издательство: Интеллект-Центр, 2015.
Презентация «МЕТОДЫ РЕШЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ» (Подготовка к ЕГЭ)
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
Описание презентации по отдельным слайдам:
Учитель математики: Смирнова Р.М. ГБОУ СОШ п.г.т. Осинки Методы решения тригонометрических уравнений
Содержание Метод замены переменной Метод разложения на множители Однородные тригонометрические уравнения С помощью тригонометрических формул: Формул сложения Формул приведения Формул двойного аргумента
Метод замены переменной С помощью замены t = sinx или t = cosx, где t ∈ [−1;1] решение исходного уравнения сводится к решению квадратного или другого алгебраического уравнения. См. примеры 1 – 3 Иногда используют универсальную тригонометрическую подстановку: t = tg
Метод разложения на множители Суть этого метода заключается в том, что произведение нескольких множителей равно нулю, если хотя бы один из них равен нулю, а другие при этом не теряют смысл: f(x) · g(x) · h(x) · … = 0 ⟺ f(x) = 0 или g(x) = 0 или h(x) = 0 и т.д. при условии существования каждого из сомножителей См. примеры 4 – 5
Однородные тригонометрические уравнения Уравнение вида a sin x + b cos x = 0 называют однородным тригонометрическим уравнением первой степени. a sin x + b cos x = 0 Замечание. Деление на cos x допустимо, поскольку решения уравнения cos x = 0 не являются решениями уравнения a sin x + b cos x = 0. : cos x a tg x + b = 0 a sin x b cos x 0 cos x + cos x = cos x tg x = – a b
Однородные тригонометрические уравнения a sin2x + b sin x cos x + c cos2x = 0 Уравнение вида a sin2x + b sin x cos x + c cos2x = 0 называют однородным тригонометрическим уравнением второй степени. : cos2x a tg2x + b tg x + c = 0 Далее, вводим новую переменную tg x = t и решаем методом замены переменной. Замечание. Если в данном уравнении а = 0 или с = 0 то, уравнение решается методом разложения на множители. + cos2x
Пример 7 Пример 6
С помощью тригонометрических формул 1. Формулы сложения: sin (x + y) = sinx cosy + cosx siny cos (x + y) = cosx cosy − sinx siny sin (x − y) = sinx cosy + cosx siny cos (x − y) = cosx cosy + sinx siny tgx + tgy tg (x + y) = 1 − tgx tgy tgx − tgy tg (x − y) = 1 + tgx tgy сtgx сtgy − 1 сtg (x + y) = сtgу + с tgх сtgx сtgy + 1 сtg (x − y) = сtgу − с tgх
С помощью тригонометрических формул 2. Формулы приведения:
Лошадиное правило В старые добрые времена жил рассеянный математик, который при поиске ответа менять или не менять название функции (синус на косинус), смотрел на свою умную лошадь, а она кивала головой вдоль той оси координат, которой принадлежала точка, соответствующая первому слагаемому аргумента π/ 2 + α или π + α. Если лошадь кивала головой вдоль оси ОУ, то математик считал, что получен ответ «да, менять», если вдоль оси ОХ, то «нет, не менять».
С помощью тригонометрических формул 3. Формулы двойного аргумента: sin 2x = 2sinx cosx cos 2x = cos2x – sin2x cos 2x = 2cos2x – 1 cos 2x = 1 – 2sin2x tg 2x = 2tgx 1 – tg2x ctg 2x = 2ctgx ctg2x – 1
С помощью тригонометрических формул 4. Формулы понижения степени: 5. Формулы половинного угла:
С помощью тригонометрических формул 6. Формулы суммы и разности:
С помощью тригонометрических формул 7. Формулы произведения:
Мнемоническое правило “Тригонометрия на ладони” Очень часто требуется знать наизусть значения cos, sin, tg, ctg для углов 0°, 30°, 45°, 60°, 90°. Но если вдруг какое-либо значение забудется, то можно воспользоваться правилом руки. Правило: Если провести линии через мизинец и большой палец, то они пересекутся в точке, называемой “лунный бугор”. Образуется угол 90°. Линия мизинца образует угол 0°. Проведя лучи из “лунного бугра” через безымянный, средний, указательный пальцы, получаем углы соответственно 30°, 45°, 60°. Подставляя вместо n: 0, 1, 2, 3, 4, получаем значения sin, для углов 0°, 30°, 45°, 60°, 90°. Для cos отсчет происходит в обратном порядке.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 932 человека из 80 регионов
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 682 человека из 75 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 308 человек из 69 регионов
Ищем педагогов в команду «Инфоурок»
Дистанционные курсы для педагогов
Самые массовые международные дистанционные
Школьные Инфоконкурсы 2022
33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
5 574 073 материала в базе
Другие материалы
- 22.11.2015
- 1710
- 3
- 22.11.2015
- 507
- 1
- 22.11.2015
- 469
- 0
- 22.11.2015
- 650
- 2
- 22.11.2015
- 1571
- 0
- 22.11.2015
- 24054
- 54
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Добавить в избранное
- 22.11.2015 6248
- PPTX 992.4 кбайт
- 384 скачивания
- Рейтинг: 5 из 5
- Оцените материал:
Настоящий материал опубликован пользователем Смирнова Раиса Михайловна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт
Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.
Автор материала
- На сайте: 6 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 85318
- Всего материалов: 32
Московский институт профессиональной
переподготовки и повышения
квалификации педагогов
Дистанционные курсы
для педагогов
663 курса от 690 рублей
Выбрать курс со скидкой
Выдаём документы
установленного образца!
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Рособрнадзор не планирует переносить досрочный период ЕГЭ
Время чтения: 0 минут
В Забайкалье в 2022 году обеспечат интернетом 83 школы
Время чтения: 1 минута
Приемная кампания в вузах начнется 20 июня
Время чтения: 1 минута
В Курганской области дистанционный режим для школьников продлили до конца февраля
Время чтения: 1 минута
Минпросвещения подключит студотряды к обновлению школьной инфраструктуры
Время чтения: 1 минута
Онлайн-конференция о создании школьных служб примирения
Время чтения: 3 минуты
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
источники:
http://www.myshared.ru/slide/1096943/
http://infourok.ru/prezentaciya-metodi-resheniya-trigonometricheskih-uravneniy-podgotovka-k-ege-604276.html
Слайд 1ЕГЭ математика
тригонометрические уравнения
Решение заданий № 13
Учитель математики Ведунова С.Н.
Муниципальное
Автономное Общеобразовательное Учреждение
средняя общеобразовательная школа №2,
пгт Серышево Амурской области.

Слайд 2а)Решите уравнение
б)Найдите корни, принадлежащие отрезку
Решение:
……………………………………………………………………………….
1способ: отбор корней по
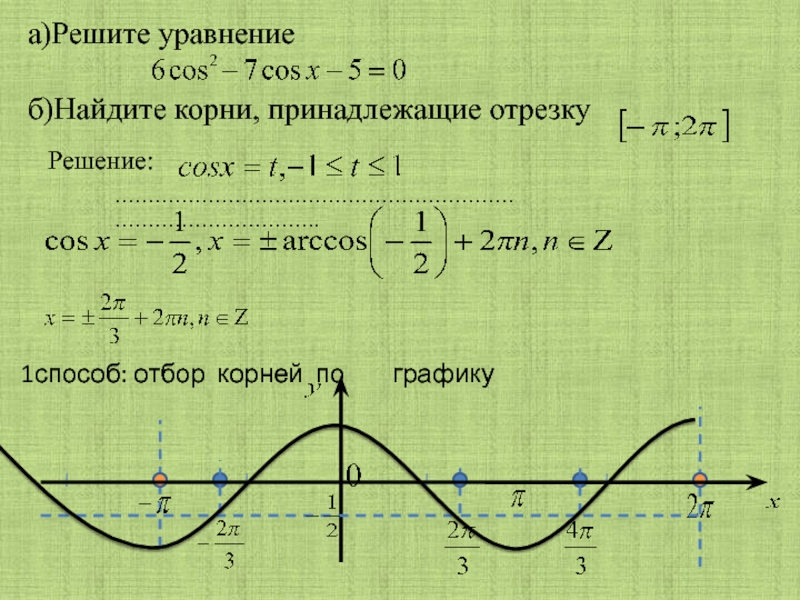
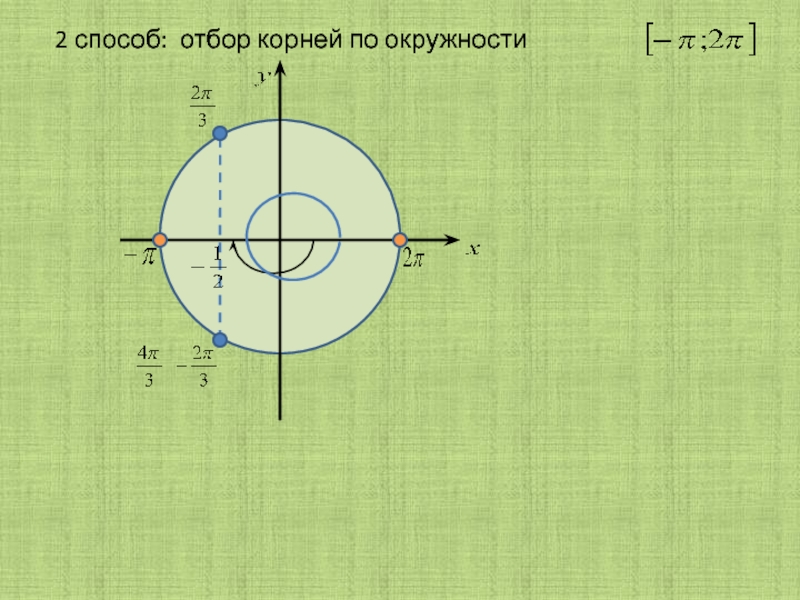
Слайд 32 способ: отбор корней по окружности
Слайд 43 способ: отбор корней неравенством

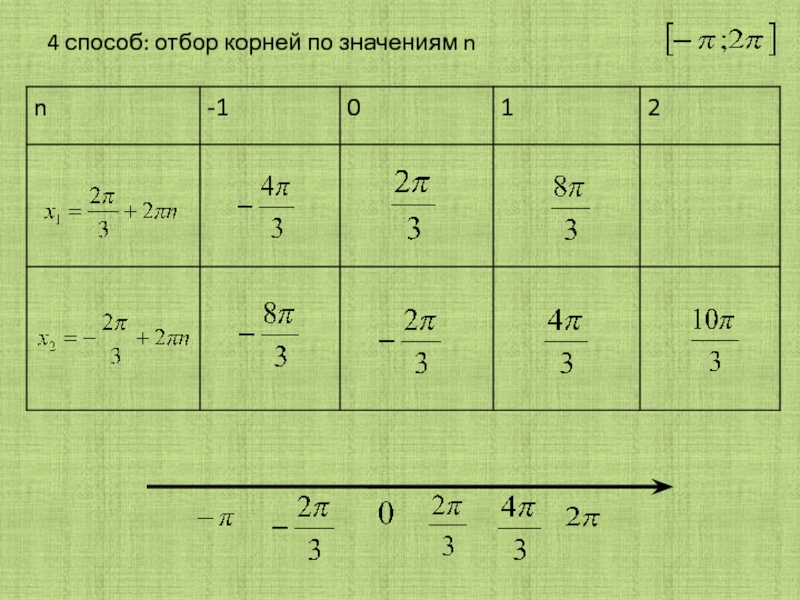
Слайд 54 способ: отбор корней по значениям n
Слайд 7a)Решить уравнение
sin2x = cosx
б)Найдите корни принадлежащие промежутку

Слайд 11Найдите все решения уравнения
принадлежащие отрезку [1;2]
2.
![ЕГЭ. Математика .Тригонометрические уравнения Найдите все решения уравнения принадлежащие отрезку [1;2] 2. Найдите все решения уравнения
принадлежащие отрезку [1;2] 2.](https://thepresentation.ru/img/tmb/3/266097/9c8110837ef2e5ebaaa6edec55e065ca-800x.jpg)
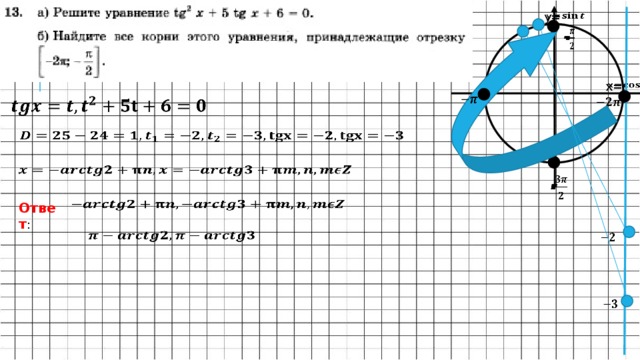
Слайд 13 а)Решите уравнение
б)Найдите все корни, принадлежащие промежутку
Решение:
3.