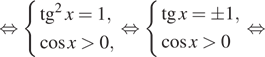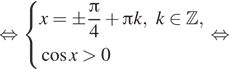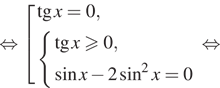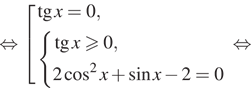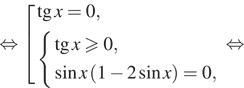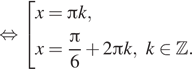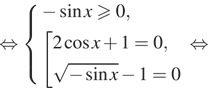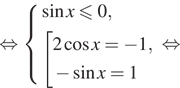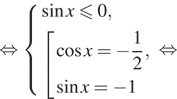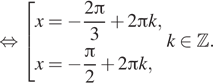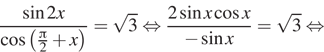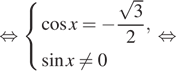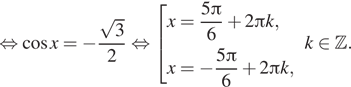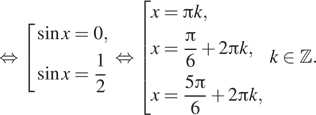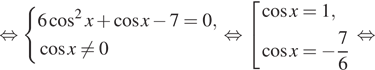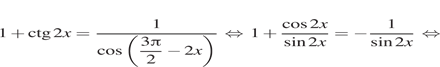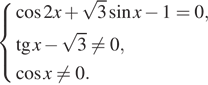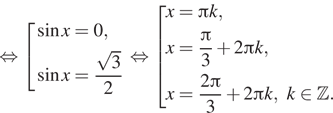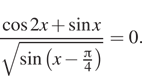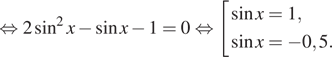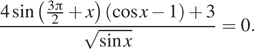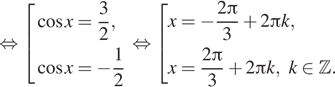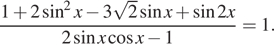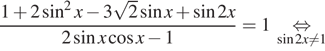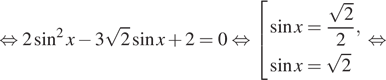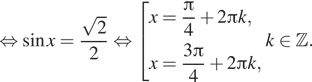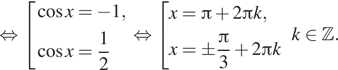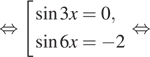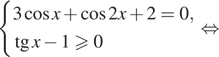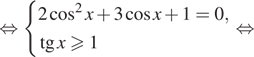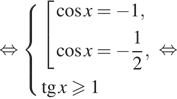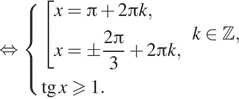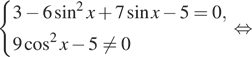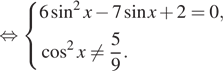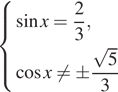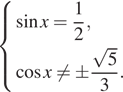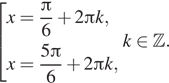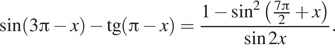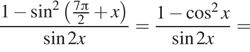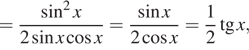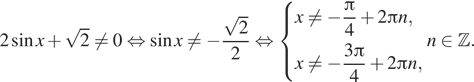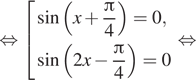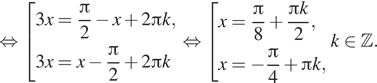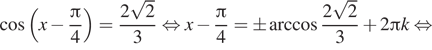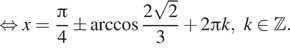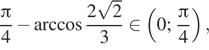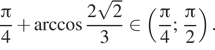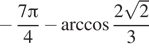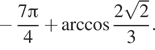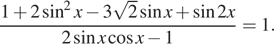СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Тригонометрические уравнения, исследование ОДЗ
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 512335
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
6 комментариев · Сообщить об ошибке · Помощь
2
Тип 12 № 512356
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Классификатор алгебры: Основное тригонометрическое тождество и его следствия, Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Использование основного тригонометрического тождества и следствий из него
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
3 комментария · Сообщить об ошибке · Помощь
3
Тип 12 № 507428
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
4
Тип 12 № 507429
а) Решите уравнение:
б) Найдите все корни этого уравнения, принадлежащие отрезку
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
5 комментариев · Сообщить об ошибке · Помощь
5
Тип 12 № 512377
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Каталог заданий.
Сложные тригонометрические уравнения, исследование ОДЗ
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
а) Решите уравнение
б) Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 40.
2
а) Решите уравнение
б) Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 46.
3
а) Решите уравнение:
б)Найдите все корни на промежутке
Источник: А. Ларин: Тренировочный вариант № 47.
4
а) Решите уравнение
б) Найдите все корни, принадлежащие промежутку
Источник: А. Ларин: Тренировочный вариант № 52.
5
а) Решите уравнение
б) Найдите сумму корней этого уравнения, принадлежащие промежутку
Источник: А. Ларин: Тренировочный вариант № 57.
Пройти тестирование по этим заданиям
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 109 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 404.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2018.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 395.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Источник: А. Ларин: Тренировочный вариант № 56.
Решите уравнение:
Решите уравнение
а) Решите уравнение
б)Найдите все корни этого уравнения, принадлежащие промежутку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Решите уравнение:
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 2.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Источник: Задания 13 (С1) ЕГЭ 2016, ЕГЭ по математике 06.06.2016. Основная волна. Юг (C часть).
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Источник: Типовые тестовые задания по математике под редакцией И.В. Ященко, 2018.
Всего: 109 1–20 | 21–40 | 41–60 | 61–80 …
Задание 2498
Дано уравнение: $$frac{2}{cos (pi -x)}-tan ^{2}x=1$$
А) Решите уравнение.
Б) Укажите корни этого уравнение, принадлежащие отрезку $$left [ -3pi; -frac{3pi}{2} right ]$$
Ответ: а) $$x=pm frac{2pi}{3}+2pi k(kin Z)$$; б)$$-frac{8pi}{3}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
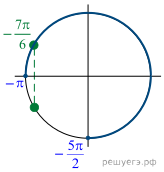
a) $$frac{2}{cos(pi-x)}-tan^{2}x=1$$ $$left{begin{matrix}cos(pi -x)neq0\xneqfrac{pi}{2}+pi k(kin Z)end{matrix}right.$$ $$Leftrightarrow$$ $$left{begin{matrix}-cos xneq0\xneqfrac{pi}{2}+pi k(kin Z)end{matrix}right.$$ $$frac{2}{-cos x}=1+tan^{2}x=frac{1}{cos^{2}x}$$ $$frac{1}{cos x}=y^{2}$$ $$-2y=y^{2}$$ $$Leftrightarrow$$ $$y^{2}+2y=0$$ $$y(y+2)=0$$ $$left{begin{matrix}y=0\y=-2end{matrix}right.$$ $$Leftrightarrow$$ $$left{begin{matrix}frac{1}{cos x}=0\frac{1}{cos x}=-2end{matrix}right.$$ $$Leftrightarrowcos x=-frac{1}{2}$$ $$Leftrightarrow$$ $$x=pm frac{2pi}{3}+2pi k(kin Z)$$
б)
$$-3pi +frac{pi}{3}=-frac{8pi}{3}$$
Задание 3034
а) Решите уравнение $$(2sin^{2}x-3sin x+1)sqrt{tan x}=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[2pi; frac{7pi}{2}]$$
Ответ: а) $$frac{pi}{6}+2pi k$$ $$pi k, kin Z$$; б) $$2pi; frac{13pi}{6}; 3pi$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$(2sin^{2}x-3sin x+1)sqrt{tan x}=0$$ $$tan xgeq 0$$ $$Rightarrow xin [pi n; frac{pi}{2}+pi n]$$ $$nin Z $$ $$left{begin{matrix}(2sin^{2}x-3sin x+1)=0\tan x=0end{matrix}right.$$ $$x=pi k, kin Z$$ $$D=9-8=1$$ $$left{begin{matrix}sin x=frac{3+1}{4}=1\sin x=frac{3-1}{4}=frac{1}{2}end{matrix}right.$$ $$left{begin{matrix}x=frac{pi}{2}+2pi n\x=frac{pi}{6}+2pi k\x=frac{5pi}{6}+2pi kend{matrix}right.$$ 1 и 2 $$notin$$ ОДЗ
Задание 3329
а) Решите уравнение $$frac{sin^{2} x +2sin x}{1-cos x}=2(1+cos x)$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$left [ -frac{pi }{2};frac{3pi }{2} right ]$$
Ответ: a) $$pi +2pi n, nin Z$$ ; б)$$pi$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Задание 3376
а) Решите уравнение $$frac{25sin2x-24x}{3tan x-4}=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{pi}{2};frac{3pi}{2}]$$
Ответ: a) $$frac{arcsinfrac{24}{25}}{2}+pi n$$; $$nin Z$$ б) $$frac{arcsinfrac{24}{25}}{2}$$; $$pi+frac{arcsinfrac{24}{25}}{2}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$3tan x-4neq0$$ $$Leftrightarrow$$ $$tan xneqfrac{4}{3}$$ $$Leftrightarrow$$ $$xneqarctanfrac{4}{3}+pi n$$, $$nin Z$$ Если $$tan xneqfrac{4}{3}$$, то $$sin xneqfrac{4}{5}$$; $$cos xneqfrac{3}{5}$$ или $$sin xneq-frac{4}{5}$$; $$cos xneq-frac{3}{5}$$ $$25sin2x-2=0$$ $$sin2x=frac{24}{25}$$ $$Leftrightarrow$$ $$left{begin{matrix}x=frac{arcsinfrac{24}{25}}{2}+pi n\x=frac{pi}{2}-frac{arcsinfrac{24}{25}}{2}+pi nend{matrix}right.$$ $$nin Z$$ $$sin2x=2sin xcos x=2cdotfrac{3}{5}cdotfrac{4}{5}=frac{24}{25}$$ Имеем совпадение, нужно сравнивать с ОДЗ
Задание 4017
а) Решите уравнение: $$frac{2-3sin x-cos2x}{6x^{2}-pi x-pi^{2}}=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{pi}{2};frac{2pi}{3}]$$
Ответ: a) $$(-1)^{n}frac{pi}{6}+pi n,nin Z$$; $$frac{pi}{2}+2pi k,kin Z(kneq0)$$; б) $$frac{pi}{6}$$
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
$$frac{2-3sin x-cos2x}{6x^{2}-pi x-pi^{2}}=0$$
ОДЗ: $$6x^{2}-pi x-pi^{2}neq0$$
$$D=pi^{2}+24pi^{2}=25pi^{2}$$
$$x_{1}neqfrac{pi+5pi}{12}=frac{pi}{2}$$
$$x_{2}neqfrac{pi-5pi}{12}=-frac{pi}{3}$$
$$2-3sin x-cos2x=0$$
$$2-3sin x-1+2sin^{2}x=0$$
$$D=9-8=1$$
$$left{begin{matrix}sin x=frac{3+1}{4}=1\sin x=frac{3-1}{4}=frac{1}{2}end{matrix}right.$$
$$sin x=1$$
$$x=frac{pi}{2}+2pi n,nin Z,nneq0$$
$$sin x=frac{1}{2}$$
$$x=frac{pi}{6}+2pi n$$
$$x=frac{5pi}{6}+2pi n$$
Задание 4067
а)Решите уравнение $$frac{2sin^{2} x-sin x}{2cos x +sqrt{3}}=0$$
б)Найдите все его корни, принадлежащие отрезку $$[pi;frac{5pi}{2}]$$
Ответ:
Задание 4069
Решите уравнение $$frac{4cos^{2} x+8sin x -7}{sqrt{-tan x}}=0$$
Ответ:
Задание 4070
Решите уравнение $$frac{(sin x -1)(2cos x +1)}{sqrt{tan x}}=0$$
Ответ:
Задание 4071
Решите уравнение $$frac{sin 2x — 2cos^{2} x}{sqrt{sin x}}=0$$
Ответ:
Задание 4072
Решите уравнение $$(sin 2x +cos x)(sqrt{3}+sqrt{3tan x})=0$$
Ответ:
Задание 4073
Решите уравнение $$frac{2cos^{2} x-5sin x +1}{2sin x — sqrt{3}}=0$$
Ответ:
Задание 4074
Решите уравнение $$(sin 2x -sin x)(sqrt{2}+sqrt{-2tan x})=0$$
Ответ:
Задание 4075
Решите уравнение $$sqrt{sin x cos x}(frac{1}{tan 2x}+1)=0$$
Ответ:
Задание 4076
а) Решите уравнение $$frac{5tan x -12}{13cos x — 5}=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[4pi;frac{11pi}{2}]$$
Ответ:
Задание 4077
Решите уравнение: $$(cos x — 1)(tan x + sqrt{3})sqrt{cos x}=0$$
Ответ:
ЕГЭ Профиль №13. Тригонометрические уравнения, содержащие ОДЗ
Задание 4067
а)Решите уравнение $$frac{2sin^{2} x-sin x}{2cos x +sqrt{3}}=0$$
б)Найдите все его корни, принадлежащие отрезку $$[pi;frac{5pi}{2}]$$
Ответ:
Задание 4069
Решите уравнение $$frac{4cos^{2} x+8sin x -7}{sqrt{-tan x}}=0$$
Ответ:
Задание 4070
Решите уравнение $$frac{(sin x -1)(2cos x +1)}{sqrt{tan x}}=0$$
Ответ:
Задание 4071
Решите уравнение $$frac{sin 2x — 2cos^{2} x}{sqrt{sin x}}=0$$
Ответ:
Задание 4072
Решите уравнение $$(sin 2x +cos x)(sqrt{3}+sqrt{3tan x})=0$$
Ответ:
Задание 4073
Решите уравнение $$frac{2cos^{2} x-5sin x +1}{2sin x — sqrt{3}}=0$$
Ответ:
Задание 4074
Решите уравнение $$(sin 2x -sin x)(sqrt{2}+sqrt{-2tan x})=0$$
Ответ:
Задание 4075
Решите уравнение $$sqrt{sin x cos x}(frac{1}{tan 2x}+1)=0$$
Ответ:
Задание 4076
а) Решите уравнение $$frac{5tan x -12}{13cos x — 5}=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[4pi;frac{11pi}{2}]$$
Ответ:
Задание 4077
Решите уравнение: $$(cos x — 1)(tan x + sqrt{3})sqrt{cos x}=0$$
Ответ:
Задание 4078
Решите уравнение $$frac{2cos^{2} x-2cos x cos 2x -1}{sqrt{sin x}}=0$$
Ответ:
Задание 4079
Решите уравнение $$frac{26cos^{2} x-23cos x +5}{13sin x -12}=0$$
Ответ:
Задание 4080
а) Решите уравнение $$7tan^{2} x — frac{1}{cos x}+1=0$$
б) Найдите все корни этого уравнения, принадлежащие промежутку $$[-frac{5pi}{2};-pi]$$
Ответ:
Задание 4081
а) Решите уравнение $$frac{1}{tan^{2} x} — frac{1}{sin x} -1 =0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-3pi;-frac{3pi}{2}]$$
Ответ:
Задание 9487
а) Решите уравнение $$frac{4}{sin^{2}(frac{7pi}{2}-x)}-frac{11}{cos x}+6=0$$
б) Найдите все корни этого уравнения, принадлежащие промежутку $$[2pi;frac{7pi}{2}]$$
Ответ:
Задание 9507
а) Решите уравнение $$tg xcdot sin^{2} x=tg x$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{2pi}{7};frac{13pi}{11}]$$
Ответ: $$pi n, nin Z$$
Задание 9660
а) Решите уравнение $$(2cos^{2}x+3sin x-3)cdot log_{2}(sqrt{2}cos x)=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-5pi;-3pi]$$.
Ответ: а)$$frac{pi}{6}+2pi k, pm frac{pi}{4}+2pi k, kin Z$$ б)$$-frac{23pi}{6}$$;$$-frac{15pi}{4}$$,$$-frac{17pi}{4}$$
Задание 9780
а) Решите уравнение $$frac{2sin^{2}x-3sin x+1}{tg x}=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-pi;frac{pi}{2}]$$
Ответ: а)$$frac{pi}{6}+2pi k$$,$$frac{pi}{6}+2pi k,kin Z$$ б)$$frac{pi}{6}$$
Задание 9800
а) Решите уравнение: $$(2sin^{2}x-cos x-1)log_{3}(-0,2sin x)=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку: $$[5pi;7pi]$$
Ответ: а)$$-frac{pi}{3}+2pi k,kin Z$$ б)$$frac{17pi}{3}$$
Задание 9927
а) Решите уравнение $$sqrt{sin(frac{pi}{4}+x)cos(frac{pi}{4}-x)}cdot cos x=frac{1}{2sqrt{2}}$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{pi}{4};pi]$$
Ответ: а) $$-frac{pi }{8}+2pi n, frac{3pi }{8}+2pi n, nin Z$$; б) $$-frac{pi }{8}; frac{3pi }{8}$$
Задание 10095
а) Решите уравнение $$frac{4sin (frac{3pi}{2}+x)(cos x-1)}{sqrt{sin x}}=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[pi;4pi]$$
Ответ: А)$$frac{pi}{2}+2pi n,nin Z$$ Б)$$frac{5pi}{2}$$
Задание 10152
а) Решите уравнение $$frac{1+2sin^{2}x-3sqrt{2}sin x+sin 2x}{2sin xcos x -1}=1$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-pi;frac{pi}{2}]$$
Ответ: А)$$frac{3pi}{4}+2pi n,nin Z$$ Б)нет решений
Задание 10192
а) Решите уравнение $$sqrt{sin^{2}x+3sin x-frac{17}{9}}=-cos x$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{3pi}{2};pi]$$
Ответ: А)$$pi-arcsin frac{2}{3}+2pi n, nin Z$$ Б)$$pi-arcsin frac{2}{3}$$, $$-pi-arcsin frac{2}{3}$$
Задание 10286
а) Решите уравнение $$(cos 2x+3sin x-2)sqrt{cos x-sin x}=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[0;pi]$$
Ответ: А)$$frac{pi}{6}+2pi n;$$ $$frac{pi}{4}+pi k,n,n in Z$$ Б)$$frac{pi}{6};frac{pi}{4}$$
Задание 10496
а) Решите уравнение $$sqrt{3-tg^{2}(frac{3x}{2})}cdot sin x-cos x=2$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-17;2]$$
Ответ: А) $$frac{2pi}{3}+2pi n, nin Z$$ Б) $$frac{-16pi}{3};-frac{10pi}{3};-frac{4pi}{3}$$
Задание 10507
а) Решите уравнение $$sqrt{ctg x}(sin^{2}x-frac{1}{4})=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$[-frac{3pi}{2};0]$$
Ответ: А)$$frac{pi}{6}+pi n, frac{pi}{2}+pi n, nin Z$$ Б)$$-frac{3pi}{2};-frac{5pi}{6};-frac{pi}{2}$$
Задание 10555
а) Решите уравнение $$frac{{cos 2x*{cos 8x }-{cos 10x } }}{{cos x }+1}=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$left[0;;pi right]$$
Ответ: а)$$frac{pi n}{8}, nin Z; nneq 8+16m, min Z$$ б)$$0;frac{pi}{8};frac{pi}{4};frac{3pi}{8};frac{pi}{2};frac{5pi}{8};frac{3pi}{4};frac{7pi}{8}$$
Задание 10615
а) Решите уравнение $$sqrt{{sin x }-{cos x }}left({ctg x }-sqrt{3}right)=0$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$left[frac{3pi }{2};3pi right]$$
Ответ: а) $$frac{pi }{4}+pi n, frac{7pi }{6}+2pi n, nin Z$$; б) $$frac{9pi }{4}$$
Задание 10635
а) Решите уравнение $$sqrt{{cos 2x }-{left({sin x }right)}^3+3}={sin x }$$
б) Укажите корни этого уравнения, принадлежащие отрезку $$left(frac{73pi }{2};left.41pi right]right.$$
Ответ: а)$$frac{pi}{2}+2pi n, nin Z$$ б)$$frac{77pi}{2};frac{81pi}{2}$$
Задание 11466
а) Решите уравнение $$ctg x-sin x-sqrt{3}cos x+frac{1}{sin x}=0$$
б) Укажите корни этого уравнения, принадлежащие промежутку $$[-0,75pi;0,5pi)$$
Ответ: а) $$frac{pi }{2}+pi n; frac{pi }{3}+2pi n, nin Z$$; б) $$-frac{pi }{2}; frac{pi }{3}$$
Задание 11748
а) Решите уравнение $$10cos^{2}frac{x}{2}=frac{11+5ctg(frac{3pi}{2}-x)}{1+tg x}$$
б) Укажите корни этого уравнения, принадлежащие промежутку $$(-2pi;-frac{3pi}{2})$$
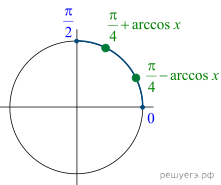
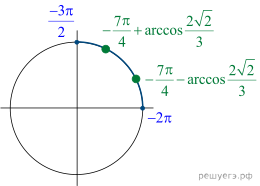
Ответ: А)$$frac{pi}{4}pm arccos frac{3sqrt{2}}{5}+2pi n,n in Z$$ Б) $$-frac{7pi}{4}pm arccos frac{3sqrt{2}}{5}$$
Задание 12671
а) Решите уравнение $$(2cos^{2} x+3sin x-3)cdot log_{2}(sqrt{2}cos x)=0$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[-5pi ; -Зpi ].$$
Ответ: а) $$frac{pi }{6}+2pi k, pm frac{pi }{4}+2pi k, k in Z$$; б) $$-frac{23pi }{6}; -frac{15pi }{4}; -frac{17pi }{4}$$
Задание 12692
а) Решите уравнение $$(2{{sin }^2 x }-cos x-1){log}_3(-0,2sin x) = 0.$$
б) Найдите все корни этого уравнения, принадлежащие отрезку $$[5pi ;7pi ]$$
Ответ: а) $$-frac{pi }{3}+2pi k, k in Z$$; б) $$frac{17pi }{3}$$
Задание 12893
а) Решите уравнение $$frac{4}{{{sin }^2 (frac{7pi }{2}-x) }}-frac{11}{{cos x }}+6=0$$
б) Найдите все корни этого уравнения, принадлежащие промежутку $$[2pi ; frac{7pi }{2}]$$
Ответ: а) $$pm frac{pi}{3}+2pi n, n in Z$$; б) $$frac{7pi }{3}$$
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1
и t=-1
получаем корни уравнения a-2pi
и b-2pi.
Bigg(a-2pi =-frac74pi +arccos frac{3sqrt 2}5,,
b-2pi =-frac74pi -arccos frac{3sqrt 2}5Bigg).
При этом -2pi
2pi Значит, эти корни принадлежат заданному промежутку left(-2pi , -frac{3pi }2right).
При остальных значениях k
и t
корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1
и tgeqslant 1,
то корни больше 2pi.
Если kleqslant -2
и tleqslant -2,
то корни меньше -frac{7pi }2.
Ответ
а)
fracpi4pm arccosfrac{3sqrt2}5+2pi k, kinmathbb Z;
б)
-frac{7pi}4pm arccosfrac{3sqrt2}5.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
а)
Решите уравнение sin left(fracpi 2+xright) =sin (-2x).
б)
Найдите все корни этого уравнения, принадлежащие промежутку ;
Показать решение
Решение
а)
Преобразуем уравнение:
cos x =-sin 2x,
cos x+2 sin x cos x=0,
cos x(1+2 sin x)=0,
cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
1+2 sin x=0,
sin x=-frac12,
x=(-1)^{k+1}cdot fracpi 6+pi k, k in mathbb Z.
б)
Корни, принадлежащие отрезку ,
найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а)
fracpi 2+pi n, n in mathbb Z;
(-1)^{k+1}cdot fracpi 6+pi k, k in mathbb Z;
б)
fracpi 2.
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Условие
не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1),
отличный от нуля. Получим уравнение frac 1{1+cos 2x}=frac 1{1+cos (pi +x)},
или уравнение 1+cos 2x=1+cos (pi +x).
Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x.
Это уравнение с помощью замены cos x=t,
где -1 leqslant t leqslant 1
сводим к квадратному: 2t^2+t-1=0,
корни которого t_1=-1
и t_2=frac12.
Возвращаясь к переменной x
, получим cos x = frac12
или cos x=-1,
откуда x=frac pi 3+2pi m,
m in mathbb Z,
x=-frac pi 3+2pi n,
n in mathbb Z,
x=pi +2pi k,
k in mathbb Z.
б)
Решим неравенства
1) -frac{3pi }2 leqslant frac{pi }3+2pi m leqslant -frac pi 2 ,
2) -frac{3pi }2 leqslant -frac pi 3+2pi n leqslant -frac pi {2,}
3) -frac{3pi }2 leqslant pi+2pi k leqslant -frac pi 2 ,
m,
n,
k in mathbb Z.
1)
-frac{3pi }2 leqslant frac{pi }3+2pi m leqslant -frac pi 2 ,
-frac32 leqslant
frac13+2m leqslant
-frac12 -frac{11}6 leqslant
2m leqslant
-frac56 ,
-frac{11}{12} leqslant m leqslant -frac5{12}.
left [-frac{11}{12};-frac5{12}right]
.
2)
-frac {3pi} 2 leqslant -frac{pi }3+2pi n leqslant -frac{pi }{2},
-frac32 leqslant -frac13 +2n leqslant -frac12 ,
-frac76 leqslant 2n leqslant -frac1{6},
-frac7{12} leqslant n leqslant -frac1{12}.
Нет целых чисел, принадлежащих промежутку left[ -frac7{12} ; -frac1{12} right].
3)
-frac{3pi }2 leqslant pi +2pi kleqslant -frac{pi }2,
-frac32 leqslant 1+2kleqslant -frac12,
-frac52 leqslant 2k leqslant -frac32,
-frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1,
тогда x=-pi.
Ответ
а)
frac pi 3+2pi m;
-frac pi 3+2pi n;
pi +2pi k,
m,
n,
k in mathbb Z;
б)
-pi .
Вы можете заказать подробное решение вашей задачи !!!
Равенство, содержащее неизвестную под знаком тригонометрической функции (`sin x, cos x, tg x` или `ctg x`), называется тригонометрическим уравнением, именно их формулы мы и рассмотрим дальше.
Простейшими называются уравнения `sin x=a, cos x=a, tg x=a, ctg x=a`, где `x` — угол, который нужно найти, `a` — любое число. Запишем для каждого из них формулы корней.
1. Уравнение `sin x=a`.
При `|a|>1` не имеет решений.
При `|a| leq 1` имеет бесконечное число решений.
Формула корней: `x=(-1)^n arcsin a + pi n, n in Z`
2. Уравнение `cos x=a`
При `|a|>1` — как и в случае с синусом, решений среди действительных чисел не имеет.
При `|a| leq 1` имеет бесконечное множество решений.
Формула корней: `x=pm arccos a + 2pi n, n in Z`
Частные случаи для синуса и косинуса в графиках.
3. Уравнение `tg x=a`
Имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arctg a + pi n, n in Z`
4. Уравнение `ctg x=a`
Также имеет бесконечное множество решений при любых значениях `a`.
Формула корней: `x=arcctg a + pi n, n in Z`
Формулы корней тригонометрических уравнений в таблице
Для синуса:


Методы решения тригонометрических уравнений
Решение любого тригонометрического уравнения состоит из двух этапов:
- с помощью преобразовать его до простейшего;
- решить полученное простейшее уравнение, используя выше написанные формулы корней и таблицы.
Рассмотрим на примерах основные методы решения.
Алгебраический метод.
В этом методе делается замена переменной и ее подстановка в равенство.
Пример. Решить уравнение: `2cos^2(x+frac pi 6)-3sin(frac pi 3 — x)+1=0`
`2cos^2(x+frac pi 6)-3cos(x+frac pi 6)+1=0`,
делаем замену: `cos(x+frac pi 6)=y`, тогда `2y^2-3y+1=0`,
находим корни: `y_1=1, y_2=1/2`, откуда следуют два случая:
1. `cos(x+frac pi 6)=1`, `x+frac pi 6=2pi n`, `x_1=-frac pi 6+2pi n`.
2. `cos(x+frac pi 6)=1/2`, `x+frac pi 6=pm arccos 1/2+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Ответ: `x_1=-frac pi 6+2pi n`, `x_2=pm frac pi 3-frac pi 6+2pi n`.
Разложение на множители.
Пример. Решить уравнение: `sin x+cos x=1`.
Решение. Перенесем влево все члены равенства: `sin x+cos x-1=0`. Используя , преобразуем и разложим на множители левую часть:
`sin x — 2sin^2 x/2=0`,
`2sin x/2 cos x/2-2sin^2 x/2=0`,
`2sin x/2 (cos x/2-sin x/2)=0`,
- `sin x/2 =0`, `x/2 =pi n`, `x_1=2pi n`.
- `cos x/2-sin x/2=0`, `tg x/2=1`, `x/2=arctg 1+ pi n`, `x/2=pi/4+ pi n`, `x_2=pi/2+ 2pi n`.
Ответ: `x_1=2pi n`, `x_2=pi/2+ 2pi n`.
Приведение к однородному уравнению
Вначале нужно данное тригонометрическое уравнение привести к одному из двух видов:
`a sin x+b cos x=0` (однородное уравнение первой степени) или `a sin^2 x + b sin x cos x +c cos^2 x=0` (однородное уравнение второй степени).
Потом разделить обе части на `cos x ne 0` — для первого случая, и на `cos^2 x ne 0` — для второго. Получим уравнения относительно `tg x`: `a tg x+b=0` и `a tg^2 x + b tg x +c =0`, которые нужно решить известными способами.
Пример. Решить уравнение: `2 sin^2 x+sin x cos x — cos^2 x=1`.
Решение. Запишем правую часть, как `1=sin^2 x+cos^2 x`:
`2 sin^2 x+sin x cos x — cos^2 x=` `sin^2 x+cos^2 x`,
`2 sin^2 x+sin x cos x — cos^2 x -` ` sin^2 x — cos^2 x=0`
`sin^2 x+sin x cos x — 2 cos^2 x=0`.
Это однородное тригонометрическое уравнение второй степени, разделим его левую и правую части на `cos^2 x ne 0`, получим:
`frac {sin^2 x}{cos^2 x}+frac{sin x cos x}{cos^2 x} — frac{2 cos^2 x}{cos^2 x}=0`
`tg^2 x+tg x — 2=0`. Введем замену `tg x=t`, в результате `t^2 + t — 2=0`. Корни этого уравнения: `t_1=-2` и `t_2=1`. Тогда:
- `tg x=-2`, `x_1=arctg (-2)+pi n`, `n in Z`
- `tg x=1`, `x=arctg 1+pi n`, `x_2=pi/4+pi n`, ` n in Z`.
Ответ. `x_1=arctg (-2)+pi n`, `n in Z`, `x_2=pi/4+pi n`, `n in Z`.
Переход к половинному углу
Пример. Решить уравнение: `11 sin x — 2 cos x = 10`.
Решение. Применим формулы двойного угла, в результате: `22 sin (x/2) cos (x/2) -` `2 cos^2 x/2 + 2 sin^2 x/2=` `10 sin^2 x/2+10 cos^2 x/2`
`4 tg^2 x/2 — 11 tg x/2 +6=0`
Применив описанный выше алгебраический метод, получим:
- `tg x/2=2`, `x_1=2 arctg 2+2pi n`, `n in Z`,
- `tg x/2=3/4`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Ответ. `x_1=2 arctg 2+2pi n, n in Z`, `x_2=arctg 3/4+2pi n`, `n in Z`.
Введение вспомогательного угла
В тригонометрическом уравнении `a sin x + b cos x =c`, где a,b,c — коэффициенты, а x — переменная, разделим обе части на `sqrt {a^2+b^2}`:
`frac a{sqrt {a^2+b^2}} sin x +` `frac b{sqrt {a^2+b^2}} cos x =` `frac c{sqrt {a^2+b^2}}`.
Коэффициенты в левой части имеют свойства синуса и косинуса, а именно сумма их квадратов равна 1 и их модули не больше 1. Обозначим их следующим образом: `frac a{sqrt {a^2+b^2}}=cos varphi`, ` frac b{sqrt {a^2+b^2}} =sin varphi`, `frac c{sqrt {a^2+b^2}}=C`, тогда:
`cos varphi sin x + sin varphi cos x =C`.
Подробнее рассмотрим на следующем примере:
Пример. Решить уравнение: `3 sin x+4 cos x=2`.
Решение. Разделим обе части равенства на `sqrt {3^2+4^2}`, получим:
`frac {3 sin x} {sqrt {3^2+4^2}}+` `frac{4 cos x}{sqrt {3^2+4^2}}=` `frac 2{sqrt {3^2+4^2}}`
`3/5 sin x+4/5 cos x=2/5`.
Обозначим `3/5 = cos varphi` , `4/5=sin varphi`. Так как `sin varphi>0`, `cos varphi>0`, то в качестве вспомогательного угла возьмем `varphi=arcsin 4/5`. Тогда наше равенство запишем в виде:
`cos varphi sin x+sin varphi cos x=2/5`
Применив формулу суммы углов для синуса, запишем наше равенство в следующем виде:
`sin (x+varphi)=2/5`,
`x+varphi=(-1)^n arcsin 2/5+ pi n`, `n in Z`,
`x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Ответ. `x=(-1)^n arcsin 2/5-` `arcsin 4/5+ pi n`, `n in Z`.
Дробно-рациональные тригонометрические уравнения
Это равенства с дробями, в числителях и знаменателях которых есть тригонометрические функции.
Пример. Решить уравнение. `frac {sin x}{1+cos x}=1-cos x`.
Решение. Умножим и разделим правую часть равенства на `(1+cos x)`. В результате получим:
`frac {sin x}{1+cos x}=` `frac {(1-cos x)(1+cos x)}{1+cos x}`
`frac {sin x}{1+cos x}=` `frac {1-cos^2 x}{1+cos x}`
`frac {sin x}{1+cos x}=` `frac {sin^2 x}{1+cos x}`
`frac {sin x}{1+cos x}-` `frac {sin^2 x}{1+cos x}=0`
`frac {sin x-sin^2 x}{1+cos x}=0`
Учитывая, что знаменатель равным быть нулю не может, получим `1+cos x ne 0`, `cos x ne -1`, ` x ne pi+2pi n, n in Z`.
Приравняем к нулю числитель дроби: `sin x-sin^2 x=0`, `sin x(1-sin x)=0`. Тогда `sin x=0` или `1-sin x=0`.
- `sin x=0`, `x=pi n`, `n in Z`
- `1-sin x=0`, `sin x=-1`, `x=pi /2+2pi n, n in Z`.
Учитывая, что ` x ne pi+2pi n, n in Z`, решениями будут `x=2pi n, n in Z` и `x=pi /2+2pi n`, `n in Z`.
Ответ. `x=2pi n`, `n in Z`, `x=pi /2+2pi n`, `n in Z`.
Тригонометрия, и тригонометрические уравнения в частности, применяются почти во всех сферах геометрии, физики, инженерии. Начинается изучение в 10 классе, обязательно присутствуют задания на ЕГЭ, поэтому постарайтесь запомнить все формулы тригонометрических уравнений — они вам точно пригодятся!
Впрочем, даже запоминать их не нужно, главное понять суть, и уметь вывести. Это не так и сложно, как кажется. Убедитесь сами, просмотрев видео.
Задача №1
Логика простая: будем поступать так, как поступали раньше не взирая на то, что теперь у тригонометрических функций стал более сложный аргумент!
Если бы мы решали уравнение вида:
То мы бы записали вот такой ответ:
Или (так как)
Но теперь в роли у нас выступаем вот такое выражение:
Тогда можно записать:
Наша с тобою цель — сделать так, чтобы слева стоял просто, без всяких «примесей»!
Давай постепенно от них избавляться!
Вначале уберём знаменатель при: для этого домножим наше равенство на:
Теперь избавимся от, разделив на него обе части:
Теперь избавимся от восьмёрки:
Полученное выражение можно расписать как 2 серии решений (по аналогии с квадратным уравнением, где мы либо прибавляем, либо вычитаем дискриминант)
Нам нужно найти наибольший отрицательный корень! Ясно, что надо перебирать.
Рассмотрим вначале первую серию:
Ясно, что если мы будем брать то в результате мы будем получать положительные числа, а они нас не интересуют.
Значит нужно брать отрицательным. Пусть.
При корень будет уже:
А нам нужно найти наибольший отрицательный!! Значит идти в отрицательную сторону здесь уже не имеет смысла. И наибольший отрицательный корень для этой серии будет равен.
Теперь рассматриваем вторую серию:
И опять подставляем: , тогда:
Не интересует!
Тогда увеличивать больше не имеет смысла! Будем уменьшать! Пусть, тогда:
Подходит!
Пусть. Тогда
Тогда — наибольший отрицательный корень!
Ответ:
Задача №2
Опять решаем, не взирая на сложный аргумент косинуса:
Теперь снова выражаем слева:
Умножаем обе стороны на
Делим обе стороны на
Всё, что осталось — это перенести вправо, изменив её знак с минуса на плюс.
У нас опять получается 2 серии корней, одна с, а другая с.
Нам нужно найти наибольший отрицательный корень. Рассмотрим первую серию:
Ясно, что первый отрицательный корень мы получим при, он будет равен и будет наибольшим отрицательным корнем в 1 серии.
Для второй серии
Первый отрицательный корень будет получен также при и будет равен. Так как, то — наибольший отрицательный корень уравнения.
Ответ:
.
Задача №3
Решаем, не взирая на сложный аргумент тангенса.
Вот, вроде бы ничего сложного, не так ли?
Как и раньше, выражаем в левой части:
Ну вот и замечательно, здесь вообще всего одна серия корней! Опять найдём наибольший отрицательный.
Ясно, что он получается, если положить. И корень этот равен.
Ответ:
Теперь попробуй самостоятельно решить следующие задачи.
Домашняя работа или 3 задачи для самостоятельного решения.
- Ре-ши-те урав-не-ние.
- Ре-ши-те урав-не-ние.
В от-ве-те на-пи-ши-те наи-мень-ший по-ло-жи-тель-ный ко-рень. - Ре-ши-те урав-не-ние.
В от-ве-те на-пи-ши-те наи-мень-ший по-ло-жи-тель-ный ко-рень.
Готов? Проверяем. Я не буду подробно описывать весь алгоритм решения, мне кажется, ему и так уделено достаточно внимания выше.
Ну что, всё правильно? Ох уж эти гадкие синусы, с ними всегда какие-то беды!
Ну что же, теперь ты умеешь решать простейшие тригонометрические уравнения!
Сверься с решениями и ответами:
Задача №1
Выразим
Наименьший положительный корень получится, если положить, так как, то
Ответ:
Задача №2
Наименьший положительный корень получится при.
Он будет равен.
Ответ:
.
Задача №3
При получаем, при имеем.
Ответ:
.
Эти знания помогут тебе решать многие задачи, с которыми ты столкнёшься в экзамене.
Если же ты претендуешь на оценку «5», то тебе просто необходимо перейти к чтению статьи для среднего уровня,
которая будет посвящена решению более сложных тригонометрических уравнений (задание С1).
СРЕДНИЙ УРОВЕНЬ
В этой статье я опишу решение тригонометрических уравнений более сложного типа
и как производить отбор их корней. Здесь я буду опираться на следующие темы:
- Тригонометрические уравнения для начального уровня (см выше).
Более сложные тригонометрические уравнения — это основа задач повышенной сложности. В них требуется как решить само уравнение в общем виде, так и найти корни этого уравнения, принадлежащие некоторому заданному промежутку.
Решение тригонометрических уравнений сводится к двум подзадачам:
- Решение уравнения
- Отбор корней
Следует отметить, что второе требуется не всегда, но все же в большинстве примеров требуется производить отбор. А если же он не требуется, то тебе скорее можно посочувствовать — это значит, что уравнение достаточно сложное само по себе.
Мой опыт разбора задач С1 показывает, что они как правило делятся на вот такие категории.
Четыре категории задач повышенной сложности (ранее С1)
- Уравнения, сводящиеся к разложению на множители.
- Уравнения, сводящиеся к виду.
- Уравнения, решаемые заменой переменной.
- Уравнения, требующие дополнительного отбора корней из-за иррациональности или знаменателя.
Говоря по-простому: если тебе попалось одно из уравнений первых трех типов
, то считай, что тебе повезло. Для них как правило дополнительно нужно подобрать корни, принадлежащие некоторому промежутку.
Если же тебе попалось уравнение 4 типа
, то тебе повезло меньше: с ним нужно повозиться подольше и повнимательнее, зато довольно часто в нем не требуется дополнительно отбирать корни. Тем не менее данный тип уравнений я буду разбирать в следующей статье, а эту посвящу решению уравнений первых трех типов.
Уравнения, сводящиеся к разложению на множители
Самое важное, что тебе нужно помнить, чтобы решать уравнения этого типа это
Как показывает практика, как правило, этих знаний достаточно. Давай обратимся к примерам:
Пример 1. Уравнение, сводящиеся к разложению на множители с помощью формул приведения и синуса двойного угла
- Ре-ши-те урав-не-ние
- Най-ди-те все корни этого урав-не-ния, при-над-ле-жа-щие от-рез-ку
Здесь, как я и обещал, работают формулы приведения:
Тогда мое уравнение примет вот такой вид:
Тогда мое уравнение примет следующую форму:
Недальновидный ученик мог бы сказать: а теперь я сокращу обе части на, получаю простейшее уравнение и радуюсь жизни! И будет горько заблуждаться!
Тригонометрическое уравнение с ОДЗ (1+cosx)(1sinx−1)=0.
Важное отличие в этом примере, что в знаменателе появился синус.
Хотя мы немного решали подобные уравнения в предыдущих уроках, стоит остановиться на ОДЗ поподробнее.
ОДЗ sinx≠0⇒x≠πk. Когда мы будем отмечать решение на круге, эту серию корней мы отметим специально проколотыми (открытыми) точками, чтобы показать, что x не может принимать такие значения.
Решение Приведем к общему знаменателю, а затем поочередно приравняем обе скобки к нулю. (1+cosx)(1−sinxsinx)=0, 1+cosx=0 или 1−sinxsinx=0, cosx=−1 или sinx=1.
1. а) Решите уравнение 5cosx+4/4tgx-3=0
б) Найдите все корни этого уравнения, принадлежащие отрезку [-4п,-5п/2]
2. Решите уравнение: 2sin2x-5sinx-3/√x+п/6=0
3. Решите уравнение: 4cos2x+8sinx-7/√tgx=0
Весь материал — в документе.
Задания 13 (C1). Уравнения
3. Тригонометрические уравнения, исследование ОДЗ
-
Решите уравнение
-
Решите уравнение
.
-
Решите систему уравнений
-
Решите уравнение
.
-
Решите уравнение
-
Решите уравнение
-
Решите уравнение
-
Решите систему уравнений
-
Решите уравнение
-
Решите уравнение
-
Решите уравнение
.
-
Решите уравнение
-
Решите уравнение
.
-
Решите уравнение
.
-
Решите уравнение
.
-
а) Решите уравнение
.
б) Найдите все корни этого уравнения, принадлежащие промежутку .
-
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
-
а) Решите уравнение
б)Найдите все корни этого уравнения, принадлежащие промежутку
-
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
-
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
-
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
-
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
-
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Тригонометрические
уравнения профильного уровня из материалов ЕГЭ.
Справочный материал.
Часть 3.
Исследование ОДЗ.
1. ) Решите уравнение
б) Найдите все корни этого уравнения,
принадлежащие отрезку
Решение. 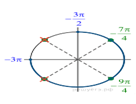
что первый множитель содержит тангенс, поэтому Второй множитель —
квадратный корень, поэтому подкоренное выражение должно быть неотрицательным.
Следовательно, область определения уравнения задается неравенством На это области второй множитель не
обращается в нуль. Рассмотрим случай, когда нулю равен первый множитель.
Последовательно получаем:
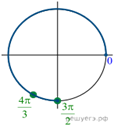
б) Корни из отрезка отберём
с помощью единичной окружности. Получаем и
Ответ: а)
б)
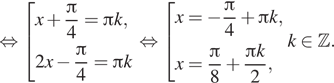
2. а) Решите уравнение б) Найдите
все корни этого уравнения, принадлежащие отрезку
Решение. 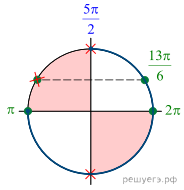
б) Корни, принадлежащие отрезку отберём
с помощью единичной окружности. Получаем и
Ответ: а)
б)
3. а) Решите уравнение: б) Найдите
все корни этого уравнения, принадлежащие отрезку
Решение.
a) Решим уравнение:
б) Корни, принадлежащие отрезку отберём
с помощью единичной окружности. Получаем и
Ответ: а)
б)
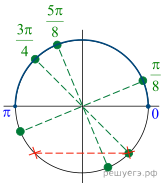
4. а) Решите уравнение 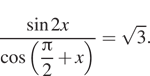
корни этого уравнения, принадлежащие отрезку
Решение. а) Используя
формулу синуса двойного угла и формулу приведения, имеем:
б) При помощи единичной окружности находим, что
отрезку принадлежит
только корень
Ответ: а) б)
5. а) ешите уравнение 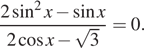
все корни этого уравнения, принадлежащие отрезку
Решение. а) Левая
часть уравнения определена при то
есть при Числитель
дроби должен быть равен нулю:
Серию нужно
отбросить. Получаем ответ:
б) При помощи тригонометрической окружности отберём
корни, лежащие на отрезке
Ответ: а) б)
6. а) Решите уравнение б) Найдите
все корни этого уравнения, принадлежащие отрезку
Решение. а) Область
определения данного уравнения задается условием
При этом условии имеем:
откуда
или
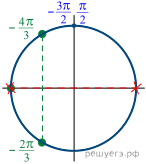
не
удовлетворяют условию а из уравнения
получаем
или
б) Из найденных решений промежутку принадлежат
числа
Ответ: а) б)
7. а) Решите уравнение б) Найдите
все корни этого уравнения, принадлежащие промежутку
Решение. а) Решим
уравнение
б) Найдем корни, лежащие в заданном отрезке, решая
двойное неравенство:
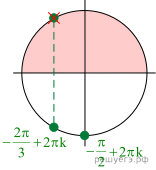
Тогда искомый корень
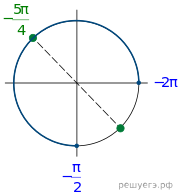
Примечание.
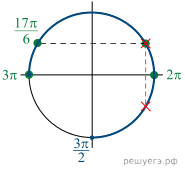
Отобрать корни можно, используя тригонометрическую окружность
(см. рис.).
Ответ: а) б)
8. а) Решите уравнение 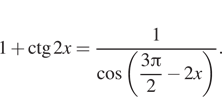
корни этого уравнения, пр инадлежащие промежутку
Решение. а) Выполним
преобразования:
Из уравнения (1) находим:
Так как решения уравнения (a) не удовлетворяют условию (2), то
окончательно получаем
б) Из решений, найденных в пункте а), промежутку принадлежит
только одно число: Ответ: а)
б)
9. а) Решите
уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. 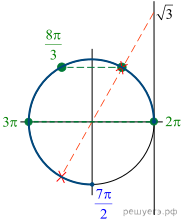
к системе:
Рассмотрим первое уравнение системы:
Условию удовлетворяют только
решения и
б) На отрезке корни
отберём с помощью единичной окружности. Получаем:
Ответ: а) б)
10. а) Решите
уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. 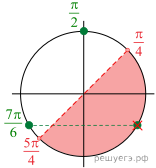
область определения уравнения:
Найдем корни числителя, используем формулу
Откуда
С учетом области определения уравнения получаем:
б) Заметим, что значит,
из первой серии корней указанному отрезку принадлежит только
Из неравенств следует,
что ни один из корней второй серии не принадлежит указанному отрезку.
Ответ: а) б)
11. а) Решите
уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. а) Дробь
равна нулю, если ее числитель равен нулю, а знаменатель отличен от нуля.
Поскольку при
условии имеем:
Корни первой серии не удовлетворяют условию положительности
синуса, поэтому решением уравнения являются только числа
б) Разность между соседними корнями в серии равна
2π. Поэтому на отрезке имеющем
длину 3π, лежит ровно одно число этой серии. Это число
Ответ: а) б)
12. а) Решите
уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. а) Знаменатель
дроби не должен обращаться в нуль, то есть Преобразуем уравнение при этом условии:
Условию удовлетворяет
только
б) Отберём корни при помощи двойного неравенства:
Указанному отрезку удовлетворяет только
Ответ: а) б)
13. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. 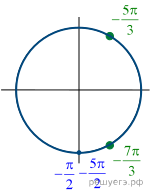
что уравнение определено при условии и
то есть
Преобразуем
его при этом условии:
В области определения лежат только
б) Отберём корни при помощи тригонометрической
окружности. Подходят
Ответ: а) б)
14. а) Решите
уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. 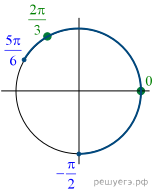
уравнение при условиях :
Ограничениям соответствует только откуда
б) Отберём корни при помощи тригонометрической
окружности. Подходят корни 0 и
Ответ: а) б)
0,
15. а) Решите
уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. 
равно нулю, когда один из множителей равен нулю, а остальные при этом
существуют. Первый множитель равен нулю, если откуда
При
всех таких х второй множитель существует, поскольку он определен для
любых значений переменной.
Рассмотрим второй случай:
Проверим выполнение условия Числа вида
не подходят, поскольку тангенс любого из них
равен нулю. Серия также
посторонняя, поскольку соответствующие точки лежат во второй четверти, где
тангенс отрицателен. Наконец, используя периодичность тангенса, его нечетность
и применяя формулу приведения, получаем, что для всех k:
поэтому серия подходит.
Объединяя случаи, заключаем, что решениями уравнения являются или
б) Отберём корни при помощи единичной окружности
(см. рис.), подходят числа и
Ответ: а) б)
16.
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие
отрезку
Решение. 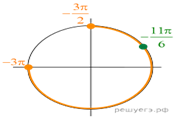
к системе:
Получаем
или
При не
выполнено условие 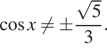
находим
б) С помощью числовой окружности отберём корни,
принадлежащие отрезку Получим
Ответ: а) б)
17.
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Решение. 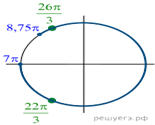
правую часть уравнения:
сокращать на можно при условии
Далее
получаем:
б) Отберём корни при помощи тригонометрической
окружности. Подходят
Ответ: а) б)
18. а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Решение. а) Уравнение
определено, если
При таких значениях переменной знаменатели дробей в левой и правой
частях уравнения равны и отличны от нуля, а значит, должны быть равны числители
этих дробей. Решим уравнение:
В области определения лежат серии корней
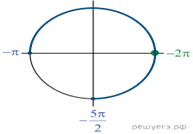
б) Отберем корни при помощи единичной окружности
(см. рис.). Подходят:
Примечание.
Выше мы решили уравнение применив формулу приведения
и
формулу разности косинусов. Можно было использовать условие равенства
косинусов:
откуда в нашем случае получаем:
19. а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие
интервалу
Решение. а) Дважды
применим к левой части уравнения формулу синуса двойного угла:
откуда получаем:
Правая часть уравнения определена, если котангенс существует и
отличен от ±1, то есть при где
Упростим
ее при этих условиях, используя формулу разности квадратов:
Используем свойство пропорции и раскроем скобки:
В силу формулы получаем:
б) Интервал можно
получить поворотом интервала на
угол –2π, поэтому достаточно найти решения, лежащие на интервале а
затем уменьшить их на –2π.
Заметим, что 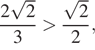
потому в силу убывания арккосинуса
Следовательно,
Интервалу принадлежат
корни на –2π меньшие, то есть числа:
и
Корни на интервале
Решить самостоятельно.
1. а) Решите уравнение: б) Найдите
все корни этого уравнения, принадлежащие отрезку
2. а) Решите уравнение: б) Найдите
все корни этого уравнения, принадлежащие отрезку
3. а) Решите уравнение 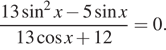
все корни этого уравнения, принадлежащие отрезку
4. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащего
отрезку
5. а) Решите
уравнение б) Найдите
все корни этого уравнения, принадлежащие отрезку
6. a) Решите уравнение б) Укажите
корни этого уравнения, принадлежащие промежутку
7. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
8. а) Решите уравнение
б) Укажите
корни этого уравнения, принадлежащие отрезку
9. а) Решите уравнение б) Укажите
корни этого уравнения, принадлежащие отрезку
10. а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие
отрезку
Ответы.
1. а) б)
2. а) б)
3. а) б)
4. а) б)
5. а) б)
6. а) б)
7. а) б)
8. а) б)
9. а) б)
10. а) б)
Скачано с www.znanio.ru