Тригонометрические уравнения разложение на множители решу егэ

Каталог заданий.
Тригонометрические уравнения, разложение на множители

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 304    1–20 | 21–40 | 41–60 | 61–80 …

Добавить в вариант

Всего: 304    1–20 | 21–40 | 41–60 | 61–80 …

Алгебра и начала математического анализа, 10 класс

Урок №47. Методы решения тригонометрических уравнений.

Перечень вопросов, рассматриваемых в теме:

• Формирование системы знаний и умений решать тригонометрические уравнения различными методами;
• Применение метода разложения на множители при решении тригонометрических уравнений;
• Применение метода оценки при решении тригонометрических уравнений;
• Прием домножения левой и правой частей уравнения на тригонометрическую функцию при решении тригонометрических уравнений.

Глоссарий по теме

Теорема — основа метода разложения на множители

Уравнение равносильно на своей области определения совокупности .

Теорема — основа метода замены переменной

Уравнение равносильно на ОДЗ совокупности уравнений

.

Основная литература:

Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. Уровни – 2-е изд. – М.: Просвещение, 2011. – 368 с.: ил. – ISBN 978-5-09-025401-4, сс.327-332

Дополнительная литература:

Шахмейстер А.Х. Тригонометрия. М.: Издательство МЦНМО : СПб.: «Петроглиф» : «Виктория плюс», 2013. – 752 с.: илл. ISBN 978-5-4439-0050-6, сс.219-221, 245-262

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

На этом уроке мы продолжаем заниматься решением тригонометрических уравнений. И здесь мы рассмотрим такие методы как разложение на множители, метод оценки, а также продолжим решать тригонометрические уравнения методом замены переменной. Кроме того, мы узнаем, как использовать домножение правой и левой частей уравнений для получения более простого уравнения, как использовать тригонометрические формулы для решения уравнений.

Сейчас выполните несколько заданий.

Задание 1.

Представьте в виде произведения:

Решение:

Используем формулы приведения, затем формулу преобразования суммы косинусов в произведение:

.

(На последнем шаге мы фактически использовали формулу двойного аргумента:

.

Ответ: .

Задание 2.

Вычислите:

Решение:

Воспользуемся формулой понижения степени и формулой преобразования произведения косинусов в сумму косинусов. Появившийся при этом общий множитель вынесем за скобки:

Воспользуемся тем, что косинус – функция четная и известным значением косинуса. В результате получим:

Ответ: 0,25

Задание 3.

Проверьте равенство:

Решение:

При выполнении этого задания будем использовать прием домножения о деления левой части на одно и то же тригонометрическое выражение.

Но сначала заметим, что .

Теперь запишем левую часть: .

теперь домножим и разделим это выражение на : .

Теперь воспользуемся формулой синуса двойного аргумента и получим:

. Теперь еще раз воспользуемся формулой двойного аргумента, предварительно домножив числитель и знаменатель на 2:

Учитывая, что , получаем: .

То есть исходное равенство верно.

Объяснение новой темы

1. Рассмотрим метод разложения на множители

Теоретической основой метода разложения на множители является теорема:

Теорема

Уравнение равносильно на своей области определения совокупности .

Для того чтобы применить эту теоремы, нужно исходное уравнение привести к виду , используя разные приемы.

Пример 1.

Решить уравнение:

Решение:

Перенесем правую часть уравнения в левую и преобразуем:

, .

Ответ: .

В этом случае мы использовали метод группировки для разложения на множители тригонометрического выражения.

Часто для преобразования выражения в произведение нужно использовать тригонометрические формулы. Рассмотрим такой пример:

Пример 2.

Решить уравнение:

Решение:

Преобразуем разность синусов в произведение:

Теперь вынесем за скобку общий множитель:

И решим каждое из двух уравнений: .

. Заметим, что вторая серия решений включается в первую. Поэтому мы можем оставить в ответе только первую серию.

Ответ: .

2. Замена переменной

Еще один метод решения тригонометрических уравнений — это метод разложения на множители. Мы уже знакомились с ним, когда решали уравнения, сводимые к квадратному или другому алгебраическому уравнению, когда решали однородные уравнения, а также знакомились с универсальной тригонометрической подстановкой. На этом уроке мы познакомимся еще с одной заменой, которая позволяет решать тригонометрические уравнения.

Рассмотрим уравнение вида:

или .

Для его решения введем новую переменную .

Тогда .

Выразим отсюда (или ).

Пример3.

Решите уравнение

Решение:

Сделаем замену . Тогда .

Вспомогательное уравнение имеет вид:

.

.

Вернемся к исходной переменной:

.

Решим каждое из этих уравнений с помощью формулы введения вспомогательного угла:

, .

Так как , то оба уравнения имеют решения:

, .

Ответ: .

3. Теперь рассмотрим метод оценки

Часто этот метод применяют в том случае, когда уравнение включает в себя функции разного типа, например, тригонометрические и показательные, и обычные преобразования на приводят к результату. Но мы рассмотрим метод оценки при решении тригонометрических уравнений. Он основан на свойстве ограниченности тригонометрических выражений.

Рассмотрим пример.

Пример 4.

Решить уравнение: .

Мы знаем, что . С другой стороны, для того чтобы произведение двух различных чисел было равно 1, то они должны быть взаимно обратными, то есть если одно из них меньше 1,то другое больше 1. Но так как косинус больше 1 быть не может, то равенство может выполняться только в двух случаях:

или .

или .

или .

Вторая система ни при каких значениях k и n не имеет решений.

Первая система имеет решения при n=3m, k=2m, поэтому ее решения, а значит, и решение уравнения:

Ответ:

Рассмотрим еще один пример, в котором метод оценки применяется для решения уравнения, правая и левая части которого являются функциями разного типа.

Пример 5.

Решите уравнение:

Решение:

Рассмотрим левую часть уравнения и преобразуем его:

.

Поэтому

Теперь рассмотрим правую часть: .

Поэтому данное уравнение решений не имеет.

Ответ: решений нет

Рассмотрим несколько задач.

Решите уравнение:

Решение:

Домножим уравнение на 2 и воспользуемся формулой понижения степени:

Теперь воспользуемся формулой преобразования суммы косинусов с произведение:

.

Теперь перенесем правую часть в левую и вынесем за скобку общий множитель:

Теперь используем формулу преобразования разности косинусов в произведение:

Теперь решим три простейших тригонометрических уравнения:

, .

В этом случае достаточно оставить первые две серии решений, так как числа вида при нечетных значениях m попадают в первую серию решений, а при четных — во вторую.

Таким образом, получаем ответ:

Ответ:

Решите уравнение:

Используя метод вспомогательного угла, оценим выражение, стоящее в левой части уравнения.

То есть будем рассматривать левую часть уравнения как выражение вида:

, где .

Получим, что

Мы знаем, что , поэтому

Поэтому уравнение решений не имеет.

Ответ: решений нет.

Рассмотрим решение более сложного уравнения методом оценки.

Решите уравнение

Запишем уравнение в виде

Преобразуем левую часть:

Так как , то

и .

Так как и , то

Равенство возможно только при одновременном выполнении условий:

.

,

.

.

, .

Решая эту систему, получим, что,  .

Ответ: ,  .

Рассмотрим еще один прием, который применяется при решении тригонометрических уравнений.

Домножение левой и правой части на тригонометрическую функцию

Рассмотрим решение уравнения:

Решение:

Домножим обе части уравнения на :

.

Заметим, что домножая обе части уравнения на выражение с переменной, мы можем получить новые корни. Проверим те значения переменной, при которой :

не являются решением исходного уравнения, поэтому мы должны будем удалить эти числа из полученного решения.

Теперь с помощью формулы синуса двойного аргумента преобразуем полученное уравнение:

Теперь перенесем правую часть в левую и преобразуем по формуле преобразования разности синусов в произведение:

, .

Учитывая, что , получим: .

Ответ: .

Примеры и разборы решений заданий тренировочного модуля

Пример 1.

A=1

подсказка

B=2

замена

C=6

Период

Ответ:

Пример 2.

Решите уравнение. Найдите коэффициенты a, b, c

Ответ:

Представим левую и правую части уравнения в виде произведения. Затем перенесём всё в левую часть и разложим на множители

a=1 ВАРИАНТ

b=7 МНОЖИТЕЛЬ

c=7 СЛАГАЕМОЕ

Ответ:

07
Апр 2012

12 Задание (2022) (C1)ВИДЕОУРОКИТРИГОНОМЕТРИЯ

Решение тригонометрических уравнений с помощью разложения на множители

|
Отзывов (12)
| Метки: решение задания С1

В данной статье остановимся кратко на решении задач C1 из ЕГЭ по математике. Эти задания представляют собой уравнения, которые требуется, во-первых, решить (то есть найти их решения, причем все), во-вторых, осуществить отбор решений по тому или иному ограничению. В последние годы на ЕГЭ по математике в заданиях C1 школьникам предлагаются для решения тригонометрические уравнения, поэтому в данной статье разобраны только они. Примеры структурированы по методам решения уравнений, от самых элементарных, до достаточно сложных.

Прежде чем перейти к разбору конкретных тригонометрических уравнений, вспомним основные формулы тригонометрии. Приведем их здесь в справочном виде.

Решение простейших тригонометрических уравнений

Решение. Используем вторую формулу на рисунке. Здесь и далее полагаем (на всякий случай, эта запись означает, что числа и принадлежат множеству целых чисел):

Другими словами, нам нужно подобрать такое число из промежутка косинус которого был бы равен Это число Используя это, получаем:

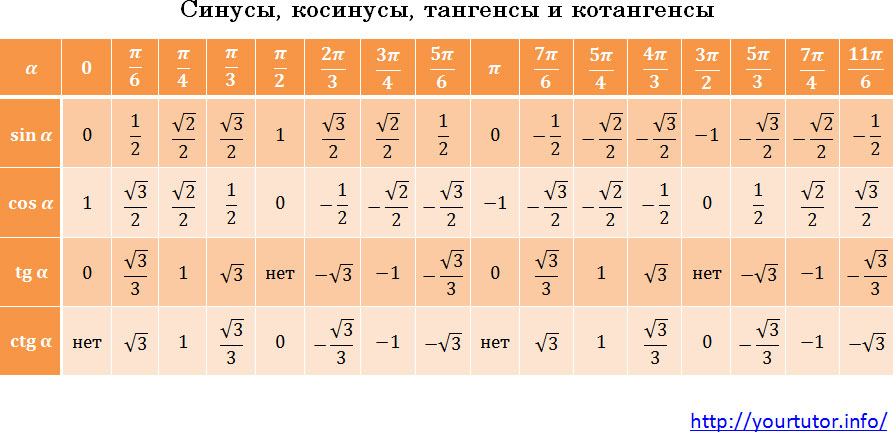
Вообще, значения тригонометрических функций от основных аргументов нужно знать. Их совсем чуть-чуть:

Хотя на самом деле запоминать их вовсе не обязательно. Существует очень простой алгоритм, используя который, можно в уме легко вычислять значения тригонометрических функций всех основных аргументов. Просто у каждого он свой. Придумайте его и для себя. Просто посмотрите на эту таблицу. Числа в ней расположены не случайным образом, определенная закономерность есть, постарайтесь ее найти.

Итак, вернемся к нашему заданию. Из полученных серий выбираем только те ответы, которые принадлежат промежутку  Воспользуемся для этого методом двойных неравенств. Вы помните, что и — целые числа:

1)

2)

Задача для самостоятельного решения №1. Найдите корни уравнения принадлежащие промежутку

Показать ответ

Решение линейных тригонометрических уравнений

Решение. Подобные уравнения решаются один весьма интересным, на мой взгляд, способом. Разделим обе части на , уравнение тогда примет вид:

Подберем такое число, синус которого равен а косинус равен Например, пусть это будет число . С учетом этого перепишем уравнение в виде:

Присмотревшись, слева от знака равенства усматриваем разложение косинуса разности и Это и есть ключ к решению. Имеем:

Осуществляем отбор решений, входящих в промежуток :

1)

2) 

Задача для самостоятельного решения №2. Найдите корни уравнения принадлежащие промежутку

Показать ответ

Решение тригонометрических уравнений методом замены переменной

Решение. Сразу оговорим ограничения, накладываемые на переменную в этом уравнении: Откуда взялось это ограничение? Правильно, функция не существует при этих значениях Используем замену переменной: Тогда уравнение принимает вид:

Переходим к обратной замене:

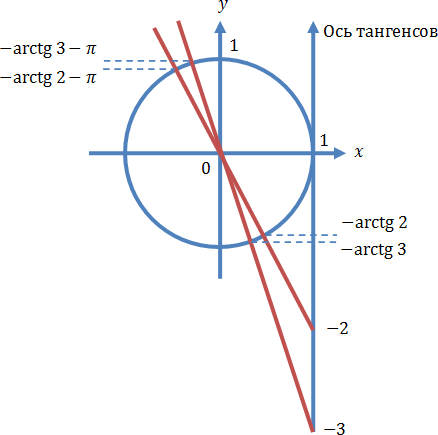
Осуществляем отбор решений. Проведем его на этот раз с использованием единичной окружности.

Из рисунка видно, что в интересующий нас промежуток входят только два значения из этих серий: Обратите внимание на один существенный момент. На рисунке точки и принадлежат оси тангенсов, а точки и — единичной окружности. Очень важно понимать, зачем это нужно для решения данной задачи.

Ответ: 

Задача для самостоятельного решения №3. Дано уравнение

a) Решите уравнение.

б) Укажите корни, принадлежащие отрезку

Показать ответ

Решение тригонометрических уравнений методом разложения на множители

Решение. Равносильными преобразования приводим уравнение к виду:

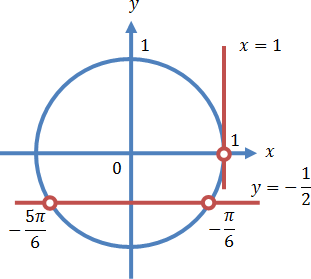
Осуществляем отбор решений с помощью единичной окружности.

Из рисунка видно, что в интересующий нас промежуток входят только два значения из всех этих серий:

Задача для самостоятельного решения №4. Дано уравнение

а) Решите уравнение.

б) Укажите корни, принадлежащие отрезку

Показать ответ

Комбинированные уравнения

При решении уравнений этого типа важно обращать внимание на область допустимых значений входящих в него переменных. Именно поэтому составители вариантов ЕГЭ не просят учеников осуществлять отбор решений из полученных серий ответов. Решение этих уравнений само собой подразумевает выполнение данной математической операции.

Решение. Данное уравнение эквивалентно следующей системе:

Обратите внимание! Писать, что нет никакой необходимости, поскольку по условию это выражение равно выражению  которое, в свою очередь, больше или равно нулю.

Решаем первое уравнение системы:

Нужно, чтобы  поразмыслив, понимаем, что поэтому из полученной серии ответов нам подходят только

Ответ:

Задача для самостоятельного решения №5. Решите уравнение:

Показать ответ

Ответ:

Решение. Данное уравение равносильно системе:

Тригонометрическая функция синус положительна в первой и второй координатной четвертях, поэтому из полученных серий выбираем только эту:

Раз уж мы с этим столкнулись, не лишним будет повторить, какие знаки принимают тригонометрические функций в различных координатных четвертях:

Ответ:

Задача для самостоятельного решения №6. Решите уравнение:

Показать ответ

Ответ:

Решение. Область допустимых значения уравнения определяется условием: то есть Разобьем решение на два случая:

1) Пусть тогда уравнение принимает вид:

Последнее равенство неверно, поэтому в данном случае решений у уравнения не будет.

2) Пусть тогда уравнение принимает вид:

Условию удовлетворяет только последняя серия.

Ответ:

Задача для самостоятельного решения №7. Решите уравнение:

Показать ответ

Ответ: 

ЕГЭ по математике 2012 позади, все в ожидании результатов, которые обещали объявить во вторник 19 июня. Сейчас уже поздно желать высоких баллов на экзаменах нынешним выпускникам. Но вот пожелать успехов сегодняшним десятиклассникам я возможности не упущу. Удачи вам в подготовке и помните, что чем раньше она начнется, тем лучше будут результаты на экзамене.

Репетитор математики
Сергей Валерьевич

P. S. Уважаемые гости! Пожалуйста, не пишите в комментариях заявки на решение ваших уравнений. К сожалению, на это у меня совершенно нет времени. Такие сообщения будут удалены. Пожалуйста, ознакомьтесь со статьёй. Возможно, в ней вы найдёте ответы на вопросы, которые не позволили вам решить своё задание самостоятельно.