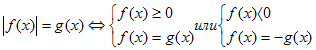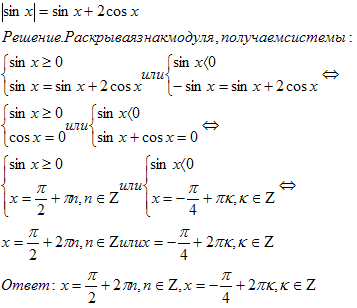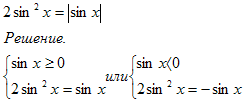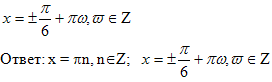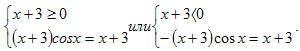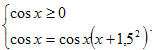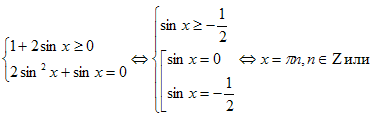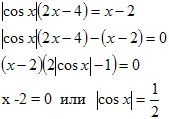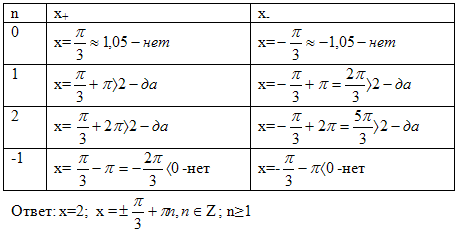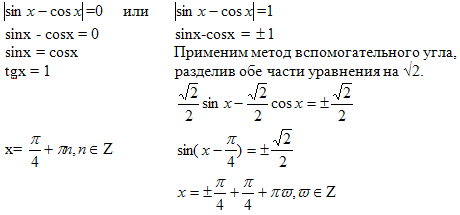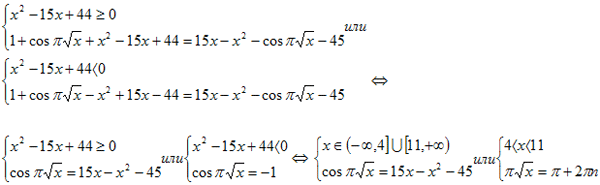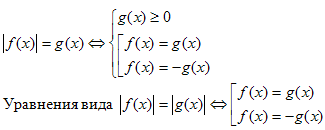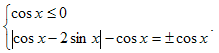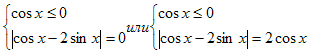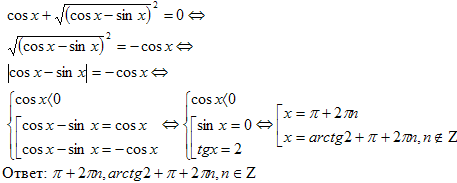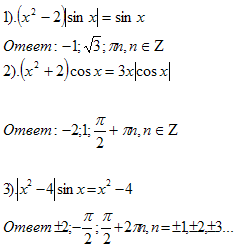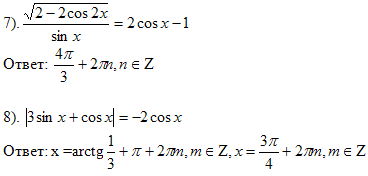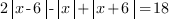Тригонометрические уравнения с модулем
Разделы: Математика
Раскрытие модуля по определению
Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а 2 x-sinx=0
sinx=0 или sinx= 
Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию sinx 2
cosx=0 или x+1,5=1 или x-1,5 = -1

Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)
Ответ:
№5. Найти все решения уравнения 
Решение. Перепишем уравнение в виде
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим
Из серии 

Решая вторую систему, получим систему 
Ответ:
№6 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия правого модуля по определению рассматривается только один случай:
х=2
Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2
№7. Решить уравнение.
Решение. ОДЗ:
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим cos2x=0, и из решений 
Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.
Ответ:
№8. Решить уравнение.
Решение. Преобразуем уравнение следующим образом:
Ответ:
№9. Решить уравнение.
Решение. Выражение под первым модулем всегда неотрицательно, и его можно сразу отбросить. Второй модуль раскрываем по определению.
Решить уравнение первой система аналитически невозможно, исследуем поведение левой и правой частей на данных промежутках. Функция f(x) =-x 2 +15x-45=(-x 2 +15x-44)-1≤-1
при 


При решении уравнения второй системы получается:


Другие способы раскрытия модулей.
Уравнения вида 
№10. Решить уравнение.
Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и правая часть, тогда cosx 21.02.2008
Задание №12. Уравнения — профильный ЕГЭ по математике
Задание 12 Профильного ЕГЭ по математике – это решение уравнений. Чаще всего, конечно, это тригонометрические уравнения. Но встречаются и другие типы – показательные, логарифмические, комбинированные.
Сейчас задание 12 Профильного ЕГЭ на решение уравнения состоят из двух пунктов: собственно решения и отбора корней на определенном отрезке.
Что нужно знать, чтобы справиться с этой задачей на ЕГЭ? Вот необходимые темы для повторения.
Что необходимо помнить при решении уравнений?
1) Помним про область допустимых значений уравнения! Если в уравнении есть дроби, корни, логарифмы или арксинусы с арккосинусами — сразу записываем ОДЗ. А найдя корни, проверяем, входят они в эту область или нет. Есть в уравнении есть — помним, что он существует, только если
2) Стараемся записывать решение в виде цепочки равносильных переходов.
3) Если есть возможность сделать замену переменной — делаем замену переменной! Уравнение сразу станет проще.
4) Если еще не выучили формулы тригонометрии — пора это сделать! Много формул не нужно. Самое главное — тригонометрический круг, формулы синусов и косинусов двойных углов, синусов и косинусов суммы (разности), понижения степени. Формулы приведения не надо зубрить наизусть! Надо знать, как они получаются.
5) Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка . От нее и будем отсчитывать. Получим:
6) Получив ответ, проверьте его правильность. Просто подставьте найденные решения в исходное уравнение!
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие промежутку
Упростим левую часть по формуле приведения.
Вынесем за скобки. Произведение двух (или нескольких) множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Видим, что указанному отрезку принадлежат решения
Как отбирать решения с помощью тригонометрического круга? Вспомним, что крайняя правая точка тригонометрического круга соответствует числам Дальше всё просто. Смотрим, какая из точек этого типа попадает в указанный в условии промежуток. И к ней прибавляем (или вычитаем) нужные значения.
Например, вы нашли серию решений , где — целое, а найти надо корни на отрезке На указанном промежутке лежит точка От нее и отсчитываем.
2. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Это уравнение — комбинированное. Кроме тригонометрии, применяем свойства степеней.
Степени равны, их основания равны. Значит, равны и показатели.
Это ответ в пункте (а).
б) Отберем корни, принадлежащие отрезку
Отметим на тригонометрическом круге отрезок и найденные серии решений.
Видим, что указанному отрезку принадлежат точки и из серии
Точки серии не входят в указанный отрезок.
А из серии в указанный отрезок входит точка
Ответ в пункте (б):
3. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Применим формулу косинуса двойного угла:
Перенесем всё в левую часть уравнения и разложим по формуле разности квадратов.
Обратите внимание: мы отметили серии решений на тригонометрическом круге. Это помогло нам увидеть, как их записать одной формулой.
б) Для разнообразия отберем корни на отрезке с помощью двойного неравенства.
Какой способ отбора корней лучше — с помощью тригонометрического круга или с помощью двойного неравенства? У каждого из них есть «плюсы» и «минусы».
Пользуясь тригонометрическим кругом, вы не ошибетесь. Вы видите и интервал, и сами серии решений. Это наглядный способ.
Зато, если интервал больше, чем один круг, удобнее отбирать корни с помощью двойного неравенства. Например, надо найти корни из серии на отрезке Это больше 10 кругов! Конечно, в таком случае лучше решить двойное неравенство.
4. а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Самое сложное здесь — область допустимых значений (ОДЗ). Условие заметно сразу. А условие появляется, поскольку в уравнении есть
Уравнение равносильно системе:
Отберем решения с помощью тригонометрического круга. Нам нужны те серии решений, для которых 
Ответ в пункте а)
б) Отметим на тригонометрическом круге найденные серии решений и отрезок
Как обычно, ориентируемся на начало круга. Видим, что указанному промежутку принадлежат точки
5. а) Решите уравнение
б) Найдите корни, принадлежащие отрезку
Выражение под корнем должно быть неотрицательно, а произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из них равен нулю.
Это значит, что уравнение равносильно системе:
Решим эту систему с помощью тригонометрического круга. Отметим на нем углы, для которых или . Заметим, что среди них находятся и углы, для которых
Числа серии не могут быть корнями исходного уравнения, т.к. для этих чисел не выполнено условие . Остальные серии решений нас устраивают.
Тогда в ответ в пункте (а) войдут серии решений:
б) Отберем корни, принадлежащие отрезку любым способом — с помощью тригонометрического круга или с помощью двойного неравенства.
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac<3pi >2;,3pi right].
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac<3pi >2;, 3pi right].
x_1=fracpi 4+2pi =frac<9pi >4,
x_2=fracpi 3+2pi =frac<7pi >3,
x_3=-fracpi 3+2pi =frac<5pi >3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac<5pi >3, frac<7pi >3, frac<9pi >4.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac<3pi >2right] ;
Решение
а) ОДЗ: begin tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin 2 sin ^2 4x-3 cos 4x=0,\tg x=0. endright.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
t_1=frac12, t_2=-2, t_2notin [-1; 1].
4x=pm fracpi 3+2pi n,
x=pm fracpi <12>+frac<pi n>2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi <12>+pi n, n in mathbb Z; x=frac<5pi ><12>+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac<3pi >2right].
Ответ
а) pi k, k in mathbb Z; fracpi <12>+pi n, n in mathbb Z; frac<5pi ><12>+pi m, m in mathbb Z.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac<7pi >2;,frac<9pi >2right].
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_<1,2>=frac<1pmsqrt 9>4=frac<1pm3>4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac<2pi >3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac<11pi >3, x_2=4pi , x_3 =frac<13pi >3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac<11pi >3, 4pi , frac<13pi >3.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac<3pi >2-xright) ><1+tgx>.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac<3pi >2right).
Решение
а) 1. Согласно формуле приведения, ctgleft( frac<3pi >2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac<11+5tgx><1+tgx>.
Заметим, что frac<11+5tgx><1+tgx>= frac<5(1+tgx)+6><1+tgx>= 5+frac<6><1+tgx>, поэтому уравнение принимает вид: 5+5 cos x=5 +frac<6><1+tgx>. Отсюда cos x =frac<dfrac65><1+tgx>, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac<3sqrt 2>5. Значит, x-fracpi 4= arccos frac<3sqrt 2>5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac<3sqrt 2>5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac<3sqrt 2>5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac<3sqrt 2>5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac<3sqrt 2>5 и b=fracpi 4-arccos frac<3sqrt 2>5.
1. Докажем вспомогательное неравенство:
Заметим также, что left( frac<3sqrt 2>5right) ^2=frac<18> <25>значит frac<3sqrt 2>5
2. Из неравенств (1) по свойству арккосинуса получаем:
Отсюда fracpi 4+0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac<3sqrt 2>5,, b-2pi =-frac74pi -arccos frac<3sqrt 2>5Bigg). При этом -2pi
-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac<3pi >2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac<7pi >2.
Ответ
а) fracpi4pm arccosfrac<3sqrt2>5+2pi k, kinmathbb Z;
б) -frac<7pi>4pm arccosfrac<3sqrt2>5.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Решение
а) Преобразуем уравнение:
cos x+2 sin x cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Задание №1174
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac<3pi ><2>; -frac<pi >2 right].
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1<1+cos 2x>=frac 1<1+cos (pi +x)>, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 ,
2) -frac<3pi >2 leqslant -frac pi 3+2pi n leqslant -frac pi
3) -frac<3pi >2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac<11>6 leqslant 2m leqslant -frac56 , -frac<11> <12>leqslant m leqslant -frac5<12>.
Нет целых чисел, принадлежащих промежутку left [-frac<11><12>;-frac5<12>right] .
2) -frac <3pi>2 leqslant -frac<pi >3+2pi n leqslant -frac<pi ><2>, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1<6>, -frac7 <12>leqslant n leqslant -frac1<12>.
Нет целых чисел, принадлежащих промежутку left[ -frac7 <12>; -frac1 <12>right].
3) -frac<3pi >2 leqslant pi +2pi kleqslant -frac<pi >2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
источники:
http://ege-study.ru/ru/ege/materialy/matematika/zadanie-12-profilnogo-ege-po-matematike-uravneniya/
http://academyege.ru/theme/trigonometricheskie-uravneniya-3.html
Раскрытие модуля по определению
Модулем числа а называется само это число а, если а ≥ 0, и число -а, если а <
0.
Согласно этому определению, в уравнениях модуль можно раскрывать следующим
образом:
№1. Решить уравнение.
№2. Решить уравнение.
Решаем уравнение первой системы:
2sin2x-sinx=0
sinx(2sinx-1)=0
sinx=0 или sinx= (оба уравнения удовлетворяют условию sinx≥0)
Решаем уравнение второй системы, и выбирая те, которые удовлетворяют условию
sinx<0,
получаем х =
Серии ответов
можно записать объединяя
№3. Решить уравнение.
Решение. Раскрывая знак модуля, получаем системы:
Решая уравнение первой системы, получим
Из значений
нужно выбрать те, которые удовлетворяют неравенству системы х ≥ -3. Это
при n=0, 1, 2, 3…
Решая уравнение второй системы, получим
Из этого множества
значений нужно выбрать те, которые удовлетворяют неравенству х < -3. Это
значения при m= -1, -2, -3…
Ответ: при n=0, 1, 2, 3…;
при m = -1, -2, -3…и х = -3
№4 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и
левая часть, поэтому, раскрывая знак модуля, получим только одну систему
Решаем уравнение системы:
соsx=cosx(x+1,5)2
cosx(1-(x+1,5)2)=0
cosx=0 или x+1,5=1 или x-1,5 = -1
х= -0,5 х = -2,5
Условию cosx≥0 не удовлетворяет х = -2,5 (3 четверть)
Ответ:
№5. Найти все решения уравнения
на отрезке [0;4].
Решение. Перепишем уравнение в виде
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим
Из серии
в нужном промежутке [0;4] лежат точки 0 и
; , а из серии
Решая вторую систему, получим систему
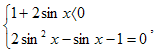
Ответ:
№6 Решить уравнение.
Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и
левая часть, тогда 2х-4≥0, 2(х-2)≥0 , х-2≥0. Если х-2≥0. то при раскрытия
правого модуля по определению рассматривается только один случай:
х=2
Выберем те корни, которые удовлетворяют условию: х-2≥0; х≥2
№7. Решить уравнение.
Решение. ОДЗ:
Раскрывая знак модуля, получаем системы:
Решая первую систему, получим cos2x=0, и из решений
надо выбрать те, при
которых sinx>0. На круге видно, что это точки вида
Решая вторую систему, получим уравнение соs2x=2,не имеющее решений.
Ответ:
№8. Решить уравнение.
Решение. Преобразуем уравнение следующим образом:
Обратная замена:
Ответ:
№9. Решить уравнение.
Решение. Выражение под первым модулем всегда неотрицательно, и его можно
сразу отбросить. Второй модуль раскрываем по определению.
Решить уравнение первой система аналитически невозможно, исследуем поведение
левой и правой частей на данных промежутках. Функция f(x) =-x2+15x-45=(-x2+15x-44)-1≤-1
при причем, f(х)= -1 в точках 4 и 11.Левая часть cos
при любых х, причем, в
точках 4 и 11 не равна -1, значит, система решений не имеет.
При решении уравнения второй системы получается:
В промежутке
только одно целое нечетное число 3, т.е
Ответ: 9
Другие способы раскрытия модулей.
Уравнения вида
можно решать и следующим способом:
№10. Решить уравнение.
Решение. Левая часть уравнения неотрицательна, значит, неотрицательна и
правая часть, тогда cosx <0, тогда уравнение равносильно системе
Рассмотрим две системы:
Решая уравнение первой системы получим: cosx-2sinx=0
Учитывая, что cosx≤0, x = arctg Вторая система решений не имеет.
Ответ: x = arctg.
№11. Решить уравнение.
cosx
Решение.
№12. Решить уравнение.
Решение. Уравнение равносильно sinx = ± cosx
Ответ:
Задачи для самостоятельного решения:
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 62 1–20 | 21–40 | 41–60 | 61–62
Добавить в вариант
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал, Задания 18 ЕГЭ–2021
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие отрезку
Источник: А. Ларин. Тренировочный вариант № 310. (Часть C)
Найдите все значения a, при каждом из которых уравнение
имеет ровно два различных корня.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург, Москва, другие города. Вариант 359 (C часть), Задания 18 ЕГЭ–2021
Дано уравнение
а) Решите уравнение.
б) Найдите его корни, принадлежащие отрезку
Источник: А. Ларин: Тренировочный вариант № 165.
Найдите все корни уравнения sin(2x) = 1, удовлетворяющие неравенству
Источник: А. Ларин: Тренировочный вариант № 130.
Найти все значения параметра а при каждом из которых уравнение имеет ровно два решения.
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Разные задачи, Задания 18 ЕГЭ–2021
Решите уравнение
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Сибирь. Вариант 302., Задания 18 (С6) ЕГЭ 2013
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402.
Найдите все значения a, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения параметра a, при каждом из которых уравнение
имеет единственное решение. Найдите это решение для каждого значения a.
Найти все значения a, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 23.04.2013. Досрочная волна. Запад. Вариант 1.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Найдите все значения а, при каждом из которых уравнение
имеет единственный корень.
Источник: ЕГЭ по математике 03.06.2013. Основная волна. Восток. Вариант 402., Задания 18 (С6) ЕГЭ 2013
Известно, что значение параметра а таково, что система уравнений
имеет единственное решение. Найдите это значение параметра a и решите систему при найденном значении параметра.
Источник: ЕГЭ по математике 2021 года. Досрочная волна., Задания 18 ЕГЭ–2021
Источник/автор: Некрасов В. Б., Гущин Д. Д. «Просвещение», 2010; Гущин Д. Д. «Учительская газета», 2013; ЕГЭ по математике − 2021
Найдите все значения a, при каждом из которых уравнение либо имеет единственное решение, либо не имеет решений.
Найдите все значения при каждом из которых уравнение
либо имеет единственное решение, либо не имеет решений.
Найдите все значения параметра при каждом из которых уравнение
имеет единственное решение.
Найдите это решение для каждого значения
Найдите все значения параметра a, при каждом из которых уравнение
имеет единственное решение. Найдите это решение для каждого значения a.
Всего: 62 1–20 | 21–40 | 41–60 | 61–62
ЕГЭ профильный уровень. №5 Тригонометрические уравнения. Задача 5
Задача 5. Решите уравнение ({text{tg}}frac{pi left( {x — 5} right)}{3} = — sqrt 3 .) В ответе напишите наименьший положительный корень.
(tgfrac{{pi left( {x — 5} right)}}{3} = — sqrt 3 ,,,,,, Leftrightarrow ,,,,,,frac{{pi left( {x — 5} right)}}{3} = — frac{pi }{3} + pi nleft| { cdot 3,,,,,, Leftrightarrow ,,,,,,pi left( {x — 5} right) = — pi + 3pi nleft| {:pi ,,,,, Leftrightarrow } right.} right.)
( Leftrightarrow ,,,,,x — 5 = — 1 + 3n,,,,,, Leftrightarrow ,,,,,x = 4 + 3n,,,,n, in ,z.)
Если (n = — 1), то (x = 1); если (n = — 2), то (x = — 2).
Следовательно, наименьший положительный корень (x = 1).
Ответ: 1.
14
Апр 2014
12 Задание (2022) (C1)ТРИГОНОМЕТРИЯУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ
Тригонометрическое уравнение с модулем
Решим тригонометрическое уравнение с модулем:
Так как уравнение содержит модуль, нам нужно этот модуль раскрыть по определению модуля.
Рассмотри два случая:
а) 
б) 
Итак.
а)
Раскрываем модуль с тем же знаком и получаем уравнение
Представим сумму косинусов в виде произведения, а правую часть уравнения разложим по формуле синуса двойного угла.
Перенесем все влево и вынесем за скобки
Отсюда 

Решим второе уравнение:
Введем замену переменной:
Решим квадратное уравнение относительно 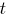
Умножим на -1:
Отсюда 
Нанесем все решения на тригонометрический круг и вспомним, что полученное уравнение «действительно» только при 



Рассмотрим второй случай:
б)
В этом случае, так как подмодульное выражение отрицательно, раскрываем модуль с противоположным знаком:
Разность косинусов представим в виде произведения.
Вынесем за скобки 
Отсюда
или
Нанесем корни на тригонометрический круг и отберем те значения, при которых выполняется условие 
Получим решения:
Объединим оба случая и получим окончательный
Ответ:
Можно объединить первую и последнюю серии решений, и тогда получим такой
Ответ:
И.В. Фельдман, репетитор по математике.
Для вас другие записи этой рубрики:
- Видеолекция «Графический метод решения задач с параметрами»
- Задание 13 из Пробного варианта, г. Брянск (2016 г.)
- Видеолекция 7. «Графический метод решения задач с параметрами»
- Тригонометрическое уравнение в целых числах
- Задание 13 из Тренировочной работы МИОО 27.04.2016 (вар. 509)
- Решение нестандартных уравнений и неравенств с помощью метода мажорант

Достаточно часто в задачах повышенной сложности встречаются тригонометрические уравнения, содержащие модуль. Большинство из них требуют эвристического подхода к решению, который совсем не знаком большинству школьников.
Предлагаемые ниже задачи призваны познакомить вас с наиболее характерными приемами решения тригонометрических уравнений содержащих модуль.
Задача 1. Найти разность (в градусах) наименьшего положительного и наибольшего отрицательного корней уравнения 1 + 2sin x · |cos x| = 0.
Решение.
Раскроем модуль:
1) Если cos x ≥ 0, то исходное уравнение примет вид 1 + 2sin x · cos x = 0.
Воспользуемся формулой синуса двойного угла, получим:
1 + sin 2x = 0; sin 2x = -1;
2x = -π/2 + 2πn, n € Z;
x = -π/4 + πn, n € Z. Так как cos x ≥ 0, то x = -π/4 + 2πk, k € Z.
2) Если cos x < 0, то заданное уравнение имеет вид 1 – 2sin x · cos x = 0. По формуле синуса двойного угла, имеем:
1 – sin 2x = 0; sin 2x = 1;
2x = π/2 + 2πn, n € Z;
x = π/4 + πn, n € Z. Так как cos x < 0, то x = 5π/4 + 2πk, k € Z.
3) Наибольший отрицательный корень уравнения: -π/4; наименьший положительный корень уравнения: 5π/4.
Искомая разность: 5π/4 – (-π/4) = 6π/4 = 3π/2 = 3 · 180°/2 = 270°.
Ответ: 270°.
Задача 2. Найти (в градусах) наименьший положительный корень уравнения |tg x| + 1/cos x = tg x.
Решение.
Раскроем модуль:
1) Если tg x ≥ 0, тогда
tg x + 1/cos x = tg x;
1/cos x = 0.
В полученном уравнении корней нет.
2) Если tg x < 0, тогда
-tg x + 1/cos x = tg x;
1/cos x – 2tg x = 0;
1/cos x – 2sin x / cos x = 0;
(1 – 2sin x) / cos x = 0;
1 – 2sin x = 0 и cos x ≠ 0.
С помощью рисунка 1 и условия tg x < 0 находим, что x = 5π/6 + 2πn, где n € Z.
3) Наименьший положительный корень уравнения 5π/6. Переведем это значение в градусы:
5π/6 = 5 · 180°/6 = 5 · 30° = 150°.
Ответ: 150°.
Задача 3. Найти количество различных корней уравнения sin |2x| = cos 2x на промежутке [-π/2; π/2].
Решение.
Запишем уравнение в виде sin|2x| – cos 2x = 0 и рассмотрим функцию y = sin |2x| – cos 2x. Так как функция является четной, то найдем ее нули при x ≥ 0.
sin 2x – cos 2x = 0; разделим обе части уравнения на cos 2x ≠ 0, получим:
tg 2x – 1 = 0;
tg 2x = 1;
2x = π/4 + πn, n € Z;
x = π/8 + πn/2, n € Z.
Воспользовавшись четностью функции, получим, что корнями исходного уравнения являются числа вида
± (π/8 + πn/2), где n € Z.
Промежутку [-π/2; π/2] принадлежат числа: -π/8; π/8.
Итак, два корня уравнения принадлежат заданному промежутку.
Ответ: 2.
Данное уравнения можно было бы решить и раскрытием модуля.
Задача 4. Найти количество корней уравнения sin x – (|2cos x – 1|)/(2cos x – 1) · sin2 x = sin2 x на промежутке [-π; 2π].
Решение.
1) Рассмотрим случай, когда 2cos x – 1 > 0, т.е. cos x > 1/2, тогда уравнение принимает вид:
sin x – sin2 x = sin2 x;
sin x – 2sin2 x = 0;
sin x(1 – 2sin x) = 0;
sin x = 0 или 1 – 2sin x = 0;
sin x = 0 или sin x = 1/2.
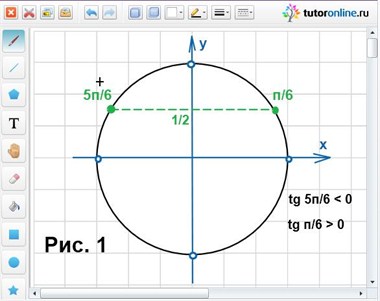
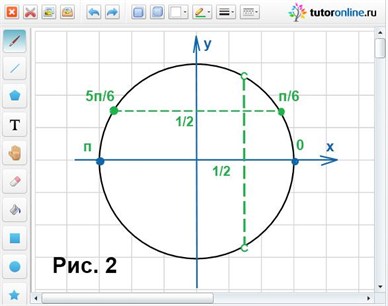
Используя рисунок 2 и условие cos x > 1/2, найдем корни уравнения:
x = π/6 + 2πn или x = 2πn, n € Z.
2) Рассмотрим случай, когда 2cos x – 1 < 0, т.е. cos x < 1/2, тогда исходное уравнение принимает вид:
sin x + sin2 x = sin2 x;
sin x = 0;
x = 2πn, n € Z.
Используя рисунок 2 и условие cos x < 1/2, находим, что x = π + 2πn, где n € Z.
Объединим два случая, получим:
x = π/6 + 2πn или x = πn.
3) Промежутку [-π; 2π] принадлежат корни: π/6; -π; 0; π; 2π.
Таким образом, заданному промежутку принадлежат пять корней уравнения.
Ответ: 5.
Задача 5. Найти количество корней уравнения (x – 0,7)2 |sin x| + sin x = 0 на промежутке [-π; 2π].
Решение.
1) Если sin x ≥ 0, то исходное уравнение принимает вид (x – 0,7)2 sin x + sin x = 0. После вынесения общего множителя sin x за скобки, получим:
sin x((x – 0,7)2 + 1) = 0; так как (x – 0,7)2 + 1 > 0 при всех действительных x, то sinx = 0, т.е. x = πn, n € Z.
2) Если sin x < 0, то -(x – 0,7)2 sin x + sin x = 0;
sin x((x – 0,7)2 – 1) = 0;
sinx = 0 или (x – 0,7)2 + 1 = 0. Так как sin x < 0, то (x – 0,7)2 = 1. Извлекаем квадратный корень из левой и правой частей последнего уравнения, получим:
x – 0,7 = 1 или x – 0,7 = -1, а значит x = 1,7 или x = -0,3.
С учетом условия sinx < 0 получим, что sin (-0,3) ≈ sin (-17,1°) < 0 и sin (1,7) ≈ sin (96,9°) > 0, значит только число -0,3 является корнем исходного уравнения.
3) Промежутку [-π; 2π] принадлежат числа: -π; 0; π; 2π; -0,3.
Таким образом, уравнение имеет пять корней на заданном промежутке.
Ответ: 5.
Заняться подготовкой к урокам или экзаменам можно при помощи различных образовательных ресурсов, которые есть в сети. В настоящее время любому 
Остались вопросы? Не знаете, как решать тригонометрические уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
12 Задание (2022) (C1)14 Задание (2022) (C3)ВИДЕОУРОКИТРИГОНОМЕТРИЯУРАВНЕНИЯ И НЕРАВЕНСТВА С МОДУЛЕМ

Давайте решим уравнение:
Вспомним, что модуль раскрывается по такому правилу:
Говоря человеческим языком, модуль выражения равен самому выражению, если оно неотрицательно, и выражению с противоположным знаком, если оно меньше нуля.
Таким образом, перед нами стоит задача раскрыть все модули в соответствии со знаками подмодульных выражений.
Будем следовать такому алгоритму:
1. Определим, в каких точках каждое подмодульное выражение меняет знак. Для этого приравняем каждое подмодульное выражение к нулю:


Мы получили три точки.
2. Нанесем их на числовую ось:
Эти три числа разбили числовую ось на четыре промежутка:



Обратите внимание, что мы включили крайние точки промежутков в оба промежутка. Ничего страшного не случится, если мы эти точки учтем два раза, главное, о них не забыть.
3. Теперь рассмотрим знаки подмодульных выражений на каждом промежутке:
Выражение 

Выражение 

Выражение 


Наше уравнение «распадается» на четыре уравнения по количеству числовых промежутков.
4. Решим уравнение на каждом промежутке:
1.
Решение уравнения на первом промежутке
2.Раскроем модули на втором промежутке:
Мы получили, что второе уравнение системы является тождеством, то есть второе равенство верно при любом действительном значении 

3. Раскроем модули на третьем промежутке:
Решение уравнения на третьем промежутке:
4. Раскроем модули на четвертом промежутке:
Решение уравнения на четвертом промежутке:
Заметим, что решения нашего уравнения на каждом промежутке принадлежали этому промежутку, то есть удовлетворяли неравенству каждой системы. Однако, так бывает не всегда, и если корень уравнения не удовлетворяет неравенству, значит, соответствующая система не имеет решений.
5. Теперь объединим полученные решения, и запишем ответ:
Ответ: -6≤х≤0, х=12
А сейчас я предлагаю вам посмотреть ВИДЕУРОК с подробным решением уравнения уровня С3:
И.В. Фельдман, репетитор по математике.
Элективный курс рассчитан на 33 часа.
Понятие модуля, решение простейших уравнений и неравенств изучается в курсе математики 6 – 9 классов фрагментарно. В практике преподавания математики в средней школе понятие абсолютной величины (модуля) впервые вводится в 6-ом классе. Здесь рассматривается определение модуля, его геометрический смысл. Модуль используют при формировании вычислительных навыков с положительными и отрицательными числами. В 7-ом классе это понятие встречается при изучении абсолютной и относительной погрешностей; в 8-ом классе – при изучении арифметического квадратного корня, векторов. А также на ЕГЭ и при поступлении в ВУЗы необходимы навыки решения уравнений, неравенств, построение графиков функций, содержащих знак абсолютной величины, хотя эти требования не входят в перечень математической подготовки учащихся средней общеобразовательной школы.
Этот элективный курс дополняет базовую программу, не нарушая её целостности. И способствует развитию логического мышления и интереса учащихся к математике.
Предлагаемый курс является развитием системы ранее приобретенных программных знаний. Его цель – создать целостное представление о теме и значительно расширить спектр задач, посильных для учащихся.
Курс ориентирован на подготовку учащихся по математике к экзаменам, углубляет базовый курс по алгебре, дает учащимся познакомиться со свойствами модулей, геометрическим местом точек модуля, решением уравнений и неравенств, содержащих несколько модулей.
В курсе заложена возможность дифференцированного обучения. Программа применима для различных групп учащихся, в том числе, не имеющих хорошей математической подготовки.
Задачи, предлагаемые в данном курсе, интересны и часто не просты в решении, что позволяет повысить учебную мотивацию учащихся и проверить свои способности к математике. Вместе с тем, содержание курса позволяет ученику любого уровня активно включиться в учебно-познавательный процесс и максимально проявить себя.
Технологии, используемые в организации элективных курсов, – деятельностно-ориентированные, чтобы способствовать процессу самоопределения учащихся и помочь учащимся адекватно оценить себя.
Цель курса:
- создание целостного представления о теме “Модуль”;
- расширить знания учащихся по теме «Решение уравнений и неравенств, построение графиков, содержащих знак модуля»;
- выработать умение решать уравнения и неравенства и строить графики элементарных функций, аналитические выражения которых содержат знак абсолютной величины.
Задачи курса:
- Систематизировать ранее полученные знания о модуле.
- Научить решать неравенства разными способами (методом интервалов, графическим способом, совокупностью систем); строить графики функции с модулями, преобразования их; решать уравнения с модулями, систему уравнений с модулями.
- Способствовать развитию интереса у учащихся к математике, развитию логического мышления обучающихся, совершенствовать и развивать математические знания и умения.
- Развивать математические, интеллектуальные способности учащихся.
Требования к уровню усвоения курса
Учащиеся должны:
- знать способы решения неравенств и уравнений и уметь их применять;
- уметь решать уравнения и неравенства, содержащие неизвестную величину под знаком модуля;
- строить графики функции с модулями.
В документе: учебно-тематический план.
Приложение:
Неравенства, содержащие модули
|
вид неравенства |
число а |
решение |
|
|
1 |
|f(x)| < a |
a £ 0 |
нет решений |
|
2 |
|f(x)| < a | |
a > 0 |
– a < f(x) < a |
|
3 |
|f(x)| £ a |
a < 0 |
нет решений |
|
4 |
|f(x)| £ a |
a = 0 |
f(x) = 0 |
|
5 |
|f(x)| £ a |
a > 0 |
– a £ f(x) £ a |
|
6 |
|f(x)| > a |
a < 0 |
множество решений совпадает с ОДЗ |
|
7 |
|f(x)| > a |
a = 0 |
f(x) ≠ 0 |
|
8 |
|f(x)| > a |
a > 0 |
f(x) < – a или f(x) > a |
|
9 |
|f(x)| ³ a |
a £ 0 |
множество решений совпадает с ОДЗ |
|
10 |
|f(x)| ≥ a |
a > 0 |
f(x) £ – a или f(x) ³ 0 |
В архиве: конспекты занятий, алгоритмы построение графиков функций, решение уравнений и неравенств, содержащих переменную под знаком модуля.
ЕГЭ Профиль №13. Уравнения с модулямиadmin2018-09-10T20:46:49+03:00
Скачать ЕГЭ Профиль №13.Уравнения с модулями в формате pdf.
Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.















































.png)