Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
$1$ радиан $={180}/{π}≈57$ градусов
$1$ градус $={π}/{180}$ радиан
Значения тригонометрических функций некоторых углов
| $α$ | $ 0$ | ${π}/{6}$ | ${π}/{4}$ | ${π}/{3}$ | ${π}/{2}$ | $π$ | |
| $sinα$ | $ 0$ | $ {1}/{2}$ | $ {√2}/{2}$ | $ {√3}/{2}$ | $ 1$ | $ 0$ | |
| $cosα$ | $ 1$ | $ {√3}/{2}$ | $ {√2}/{2}$ | $ {1}/{2}$ | $ 0$ | $ -1$ | |
| $tgα$ | $ 0$ | $ {√3}/{3}$ | $ 1$ | $ √3$ | $ -$ | $ 0$ | |
| $ctgα$ | $ -$ | $ √3$ | $ 1$ | $ {√3}/{3}$ | $ 0$ | $ -$ |
Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
Знаки тригонометрических функций по четвертям
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить, что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ (${π}/{2}$ и ${3π}/{2}$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
$сos(90° + α)=sinα$
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.
$сos(90° + α)= — sinα$ — это конечный результат преобразования
Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Тригонометрические тождества
- $tgα={sinα}/{cosα}$
- $ctgα={cosα}/{sinα}$
- $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
$sinα=±√{1-cos^2α}$
$cosα=±√{1-sin^2α}$
- $tgα·ctgα=1$
- $1+tg^2α={1}/{cos^2α}$
- $1+ctg^2α={1}/{sin^2α}$
Вычислить $sin t$, если $cos t = {5}/{13} ; t ∈({3π}/{2};2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈({3π}/{2};2π)$ -это четвертая четверть, то синус в ней имеет знак минус
$sint=-√{1-cos^2t}=-√{1-{25}/{169}}=-√{{144}/{169}}=-{12}/{13}$
Формулы двойного угла
- $sin2α=2sinα·cosα$
- $cos2α=cos^2α-sin^2α=2cos^2α-1=1-2sin^2α$
- $tg2α={2tgα}/{1-tg^2α}$
Формулы суммы и разности
$cosα+cosβ=2cos{α+β}/{2}·cos{α-β}/{2}$
$cosα-cosβ=2sin{α+β}/{2}·sin{β-α}/{2}$
$sinα+sinβ=2sin{α+β}/{2}·cos{α-β}/{2}$
$sinα-sinβ=2sin{α-β}/{2}·cos{α+β}/{2}$
Формулы произведения
$cosα·cosβ={cos(α-β)+cos(α+β)}/{2}$
$sinα·sinβ={cos(α-β)-cos(α+β)}/{2}$
$sinα·cosβ={sin(α+β)+sin(α-β)}/{2}$
Формулы сложения
$cos(α+β)=cosα·cosβ-sinα·sinβ$
$cos(α-β)=cosα·cosβ+sinα·sinβ$
$sin(α+β)=sinα·cosβ+cosα·sinβ$
$sin(α-β)=sinα·cosβ-cosα·sinβ$
Вычислить $sin12cos18+cos12sin18$
Данное выражение является синусом суммы
$sin12cos18+cos12sin18= sin(12+18)=sin30=0.5$
Задача (Вписать в ответ число)
Вычислить $sin{5π}/{12} cos {π}/{12}+cos {π}/{12} sin {5π}/{12}$
Решение:
Данное выражение является синусом суммы
$sin {5π}/{12} cos {π}/{12}+cos {π}/{12} sin {5π}/{12}=sin({π}/{12}+{5π}/{12})=sin {6π}/{12}=sin {π}/{2}=1$
Ответ: $1$
Обратные тригонометрические функции и простейшие тригонометрические уравнения
Арккосинус
Если, $|а|≤1$, то $arccos а$ – это такое число из отрезка $[0;π]$, косинус которого равен $а$.
Если, $|а|≤1$, то $arccos а = t ⇔ {table cos (t)=a; ≤t≤π;$
$arcos(-a) = π-arccosa$, где $0≤а≤1$
Уравнение вида $cos t=a$, eсли, $|а|≤1$, имеет решение
$t=±arccos a+2πk; k∈Z$
Частные случаи
$cos t =1, t = 2πk;k∈Z$
$cos t = 0, t = {π}/{2}+πk;k∈Z$
$cos t = -1, t=π+2πk;k∈Z$
Найдите наименьший положительный корень уравнения $сos{2πx}/{3}=-{√3}/{2}$
$сos{2πx}/{3}=-{√3}/{2}$
${2πx}/{3}=±arccos(-{√3}/{2})+2πk;kϵZ$
${2πx}/{3}=±(π-arccos{√3}/{2})+2πk;kϵZ$
${2πx}/{3}=±(π-{π}/{6})+2πk;kϵZ$
${2πx}/{3}=±{5π}/{6} +2πk;kϵZ$
Далее избавимся от всех величин, мешающих иксу. Для этого разделим обе части уравнения на ${2π}/{3}$
$x=±{5π·3}/{6·2π} +{2π·3}/{2π}k$
$x=±1,25+3k$
Чтобы найти наименьший положительный корень, подставим вместо $k$ целые значения
$k=0$
$x_1= -1,25$
$x_2=1,25$
$к=1$
$х_1=3-1,25=1,75$
$х_2=3+1,25=4,25$
Нам подходит $1,25$ – это и есть результат
Ответ: $1,25$
Арксинус
Если, $|а|≤1$, то $arcsin a$ – это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, синус которого равен $а$.
Если, $|а|≤1$, то $arcsin a = t ⇔ {table sint=a; -{π}/{2}≤t≤{π}/{2};$
$arcsin(-a)= — arcsin a$, где $0≤а≤1$
Если, $|а|≤1$, то уравнение $sin t =a$ можно решить и записать двумя способами:
$1. t_1 = arcsin a+2πk;k∈Z$
$t_2 = (π- arcsin a)+ 2πk;k∈Z$
$2. t=(-1)^n arcsin a+πn; n∈Z$
$3.$ Частные случаи
$sin t = 0, t=πk;k∈Z$
$sin t = 1, t={π}/{2}+2πk;k∈Z$
$sin t = -1,t=-{π}/{2}+2πk;k∈Z$
Арктангенс
$arctg a$ — это такое число, из отрезка $[-{π}/{2};{π}/{2}]$, тангенс которого равен $а$.
$arctg a = t ⇔ {table tgt=a; -{π}/{2}≤t≤{π}/{2};$
$arctg(-a)= — arctg a$
Уравнение $tg t = a$ имеет решение $t= arctg a+πk;k∈Z$
Тригонометрия для многих старшеклассников представляется сложной темой. Но на самом деле это не так. Тригонометрия проста и логична. Главное – начать с самых основ. Вспомнить, что такое градусы и радианы. Что такое синус и что такое косинус для произвольного угла.
Тригонометрию можно понять! И мы поможем вам это сделать. Ведь понимание намного лучше зубрежки. Читайте статьи этого раздела:
New Задачи из сборников Ященко, 2021 год
Измерение углов: градусы и радианы
Тригонометрический круг: вся тригонометрия на одном рисунке
Тригонометрические формулы
Формулы приведения
Все формулы тригонометрии
Тригонометрические функции
Обратные тригонометрические функции
Простейшие тригонометрические уравнения, 1
Простейшие тригонометрические уравнения, 2
Тригонометрические уравнения. Методы решения
Повторим самое главное в тригонометрии.
— Выучи, что такое синус и что такое косинус произвольного угла.
Из курса геометрии ты помнишь, что синус острого угла в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе, а косинус – отношение прилежащего катета к гипотенузе. Однако это частные случаи для углов, больших нуля и меньших 90 градусов. А мы говорим о произвольном угле. Определения синуса и косинуса произвольного угла – в этом разделе.
— Тригонометрический круг, или тригонометрическая окружность, – твоя универсальная шпаргалка. Значения синусов и косинусов основных углов, знаки синуса и косинуса в четвертях, четность и нечетность синуса и косинуса и многое другое – на тригонометрическом круге.
— Формулы приведения не надо зубрить наизусть! Надо понять, как они получаются.
— Сколько формул тригонометрии нужно знать, чтобы уверенно решать задачи? Три – это мало. 100 – это много. В нашей таблице 29 формул. Их хватит для решения любой задачи ЕГЭ. И на первом курсе вуза тоже пригодится!
— Как решать тригонометрические уравнения? Не спеши учить формулы. Сначала разберись, почему их решения именно такие. Выучи определения и свойства обратных тригонометрических функций – арксинуса, арккосинуса, арктангенса и арккотангенса.
И тренируйся на реальных задачах ЕГЭ!
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Тригонометрия» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Методические материалы по математике, нацеленные главным образом на подготовку к ЕГЭ.
Алгебра и анализ
Метод интервалов: interval.pdf
Уравнения и неравенства с модулем: modul.pdf
Что такое функция: function.pdf
Чтение графика функции: grafik.pdf
Степени и корни: power.pdf
Производная: der.pdf
Геометрический смысл производной: dergeom.pdf
Тригонометрия
Тригонометрический круг: trigcircle.pdf
Тригонометрические формулы: trigform.pdf
Простейшие тригонометрические уравнения. 1: treq1.pdf
Простейшие тригонометрические уравнения. 2: treq2.pdf
Тригонометрические уравнения: trigequations.pdf
Углы в тригонометрии: trigangles.pdf Задачи: protrigangles.pdf
Тригонометрическая окружность: trigok.pdf Задачи: protrigok.pdf
Тригонометрические функции. Синус и косинус: sincos.pdf
Тригонометрические функции. Тангенс и котангенс: tangens.pdf Задачи: protrigfun.pdf
Основное тригонометрическое тождество: ott.pdf Задачи: proott.pdf
Формулы сложения: fadd.pdf Задачи: profadd.pdf
Формулы приведения: fpriv.pdf Задачи: profpriv.pdf
Формулы двойного и половинного угла: fda.pdf Задачи: profda.pdf
Суммы и произведения тригонометрических функций: trigsum.pdf Задачи: protrigsum.pdf
Тригонометрические формулы (резюме): trigform.pdf
Обратные тригонометрические функции: trigeqprost.pdf
Тригонометрические уравнения: trigequations.pdf
Планиметрия
О первичных понятиях, или Зачем аксиомы в геометрии: primaries.pdf
Стереометрия
Многогранники в задаче С2: sm.pdf
Пирамида: piramida.pdf
Призма: prizma.pdf
Взаимное расположение прямых в пространстве: ll.pdf
Угол между скрещивающимися прямыми: lla.pdf Задачи: prolla.pdf
Взаимное расположение прямой и плоскости: lp.pdf
Теорема о трёх перпендикулярах: ttp.pdf
Угол между прямой и плоскостью: lpa.pdf Задачи: lpa.pdf
Взаимное расположение плоскостей: pp.pdf
Угол между плоскостями: ppa.pdf Задачи: proppa.pdf
Расстояние от точки до прямой: dpl.pdf Задачи: prodpl.pdf
Расстояние от точки до плоскости: dpp.pdf Задачи: prodpp.pdf
Расстояние между скрещивающимися прямыми: dll.pdf Задачи: prodll.pdf
Метод объёмов: vol.pdf
Задачи на сечения многогранников: prosec.pdf
Игорь Вячеславович Яковлев,
mathus.ru
Радианное измерение углов
Один радиан равен центральному углу окружности, длина дуги которого равна радиусу этой окружности.
|
Углы в градусах |
φ° |
30° |
45° |
60° |
90° |
180° |
270° |
360° |
|
Углы в радианах |
π/180° ∙ φ° |
π/6 |
π/4 |
π/3 |
π/2 |
π |
3/2π |
2π |
Значения тригонометрических функций некоторых углов
|
α |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
π |
3/2π |
|
sin α |
0 |
1/2 |
√2/2 |
√3/2 |
1 |
0 |
-1 |
|
cos α |
1 |
√3/2 |
√2/2 |
1/2 |
0 |
-1 |
0 |
|
tg α |
0 |
√3/3 |
1 |
√3 |
— |
0 |
— |
|
ctg α |
— |
√3 |
1 |
√3/3 |
0 |
— |
0 |
Основные тригонометрические тождества
Формулы суммы и разности аргументов
Формулы двойного и тройного аргументов
Выражение тригонометрических функций через тангенс половинного угла
Если х ≠ π + 2πk, k ∈ Z, то
Преобразование суммы и разности тригонометрических функций в произведение
a φ определяется из формулы
a φ определяется из формулы
Преобразование произведения тригонометрических функций в сумму
Определение обратных тригонометрических функций
*Свойства обратных тригонометрических функций
Некоторые значения обратных тригонометрических функций
|
x |
0 |
1/2 |
√2/2 |
√3/2 |
1 |
-1 |
|
arcsin x |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
-π/2 |
|
arccos x |
π/2 |
π/3 |
π/4 |
π/6 |
0 |
π |
|
x |
0 |
√2/3 |
1 |
√3 |
|
arctg x; |
0 |
π/6 |
π/4 |
π/3 |
|
arcctg x |
π/2 |
π/3 |
π/4 |
π/6 |
Формулы для решения простейших тригонометрических уравнений
(blacktriangleright) Рассмотрим прямоугольную систему координат и в ней окружность с единичным радиусом и центром в начале координат.
Угол в (1^circ) — это такой центральный угол, который опирается на дугу, длина которой равна (dfrac1{360}) длины всей окружности.
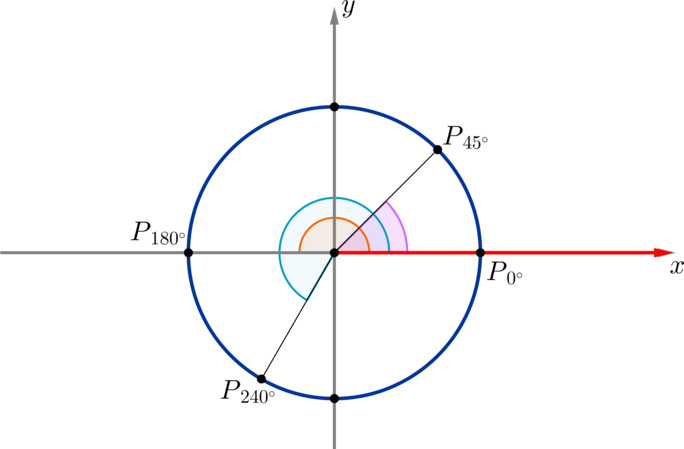
(blacktriangleright) Будем рассматривать на окружности такие углы, у которых вершина находится в центре окружности, а одна сторона всегда совпадает с положительным направлением оси (Ox) (на рисунке выделено красным).
На рисунке таким образом отмечены углы (45^circ, 180^circ,
240^circ):
Заметим, что угол (0^circ) — это угол, обе стороны которого совпадают с положительным направлением оси (Ox).
Точку, в которой вторая сторона такого угла (alpha) пересекает окружность, будет называть (P_{alpha}).
Положение точки (P_{0}) будем называть начальным положением.
Таким образом, можно сказать, что мы совершаем поворот по окружности из начального положения (P_0) до положения (P_{alpha}) на угол (alpha).
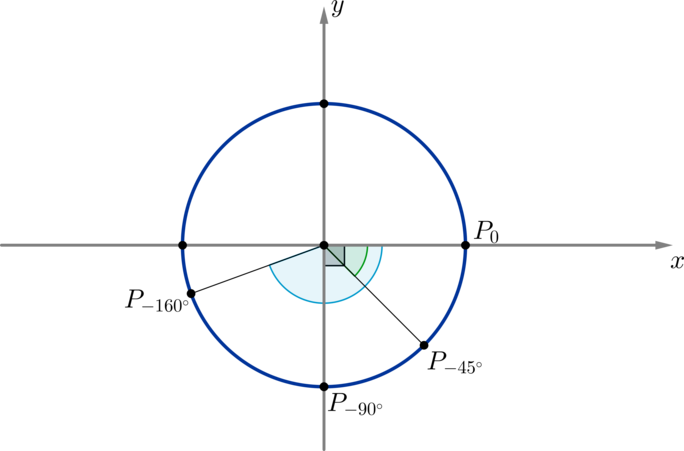
(blacktriangleright) Поворот по окружности против часовой стрелки — это поворот на положительный угол. Поворот по часовой стрелке — это поворот на отрицательный угол.
Например, на рисунке отмечены углы (-45^circ, -90^circ,
-160^circ):
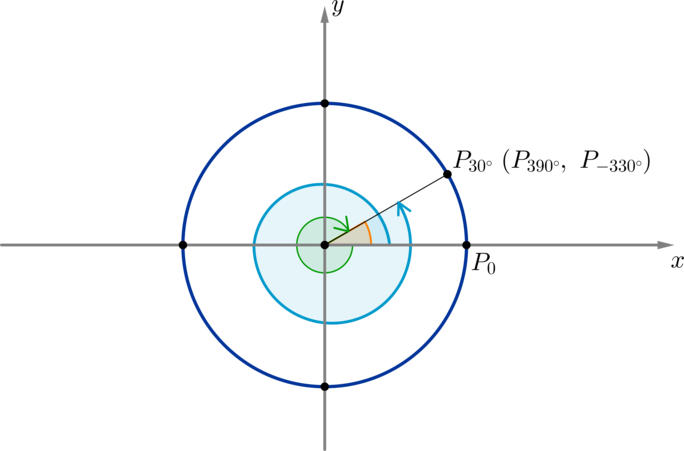
(blacktriangleright) Рассмотрим точку (P_{30^circ}) на окружности. Для того, чтобы совершить поворот по окружности из начального положения до точки (P_{30^circ}), необходимо совершить поворот на угол (30^circ) (оранжевый). Если мы совершим полный оборот (то есть на (360^circ)) и еще поворот на (30^circ), то мы снова попадем в эту точку, хотя уже был совершен поворот на угол (390^circ=360^circ+30^circ) (голубой). Также попасть в эту точку мы можем, совершив поворот на (-330^circ) (зеленый), на (750^circ=360^circ+360^circ+30^circ) и т.д.
Таким образом, каждой точке на окружности соответствует бесконечное множество углов, причем отличаются эти углы друг от друга на целое число полных оборотов ((ncdot360^circ, ninmathbb{Z})).
Например, угол (30^circ) на (360^circ) больше, чем угол (-330^circ), и на (2cdot 360^circ) меньше, чем угол (750^circ).
Все углы, находящиеся в точке (P_{30^circ}) можно записать в виде: (alpha=30^circ+ncdot 360^circ, ninmathbb{Z}).
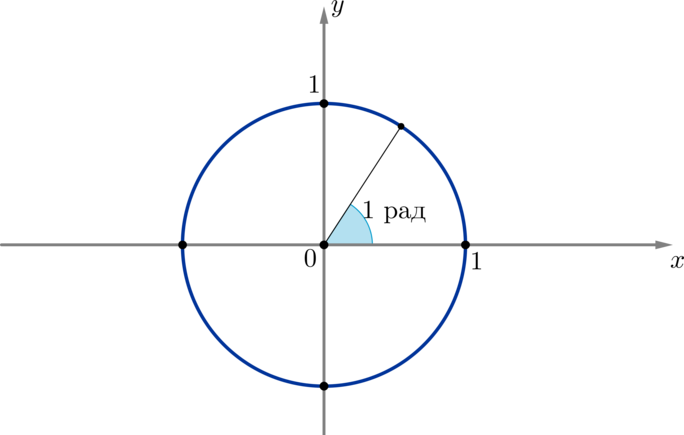
(blacktriangleright) Угол в (1) радиан — это такой центральный угол, который опирается на дугу, длина которой равна радиусу окружности:
Т.к. длина всей окружности радиусом (R) равна (2pi R), а в градусной мере — (360^circ), то имеем (360^circ=2pi cdot
1textbf{ рад}), откуда [180^circ=pi textbf{ рад}] Это основная формула, с помощью которой можно переводить градусы в радианы и наоборот.
Пример 1. Найти радианную меру угла (60^circ).
Т.к. (180^circ = pi Rightarrow 1^circ = dfrac{pi}{180}
Rightarrow 60^circ=dfrac{pi}3)
Пример 2. Найти градусную меру угла (dfrac34 pi).
Т.к. (pi=180^circ Rightarrow dfrac34 pi=dfrac34 cdot
180^circ=135^circ).
Обычно пишут, например, не (dfrac{pi}4 text{ рад}), а просто (dfrac{pi}4) (т.е. единицу измерения “рад” опускают). Обратим внимание, что обозначение градуса при записи угла не опускают. Таким образом, под записью “угол равен (1)” понимают, что “угол равен (1) радиану”, а не “угол равен (1) градусу”.
Т.к. (pi thickapprox 3,14 Rightarrow 180^circ thickapprox 3,14
textbf{ рад} Rightarrow 1 textbf{ рад} thickapprox 57^circ).
Такую приблизительную подстановку делать в задачах нельзя, но знание того, чему приближенно равен (1) радиан в градусах часто помогает при решении некоторых задач. Например, таким образом проще найти на окружности угол в (5) радиан: он примерно равен (285^circ).
(blacktriangleright) Из курса планиметрии (геометрии на плоскости) мы знаем, что для углов (0<alpha< 90^circ) определены синус, косинус, тангенс и котангенс следующим образом:
если дан прямоугольный треугольник со сторонами (a, b, c) и углом (alpha), то:
Т.к. на единичной окружности определены любые углы (alphain(-infty;+infty)), то нужно определить синус, косинус, тангенс и котангенс для любого угла.
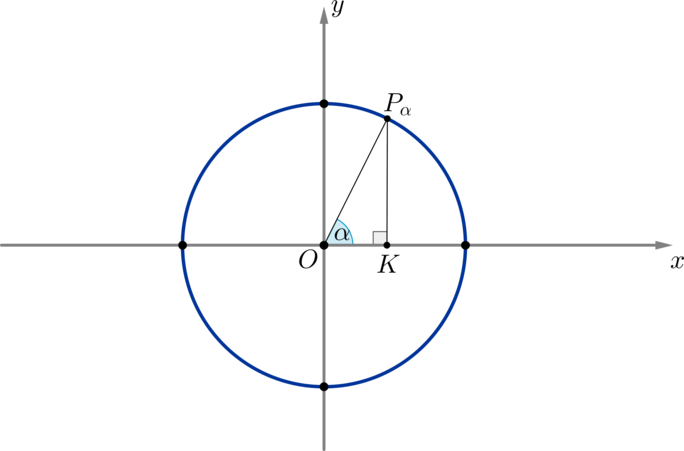
Рассмотрим единичную окружность и на ней угол (alpha) и соответствующую ему точку (P_{alpha}):
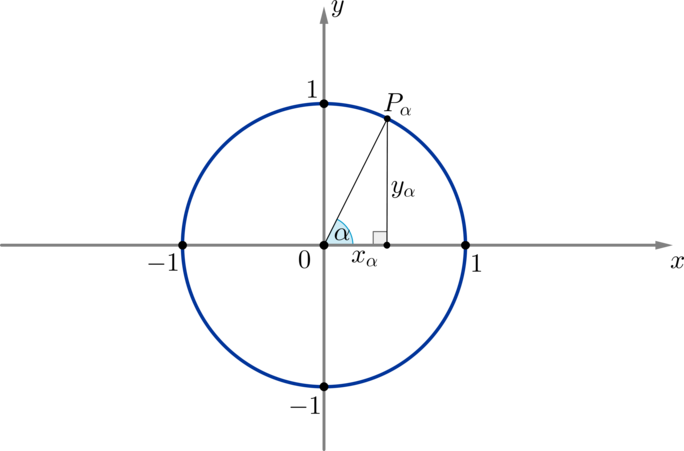
Опустим перпендикуляр (P_{alpha}K) из точки (P_{alpha}) на ось (Ox). Мы получим прямоугольный треугольник (triangle OP_{alpha}K), из которого имеем: [sinalpha=dfrac{P_{alpha}K}{P_{alpha}O} qquad cos alpha=dfrac{OK}{P_{alpha}O}] Заметим, что отрезок (OK) есть не что иное, как абсцисса (x_{alpha}) точки (P_{alpha}), а отрезок (P_{alpha}K) — ордината (y_{alpha}). Заметим также, что т.к. мы брали единичную окружность, то (P_{alpha}O=1) — ее радиус.
Таким образом, [sinalpha=y_{alpha}, qquad cos alpha=x_{alpha}]
Таким образом, если точка (P_{alpha}) имела координаты ((x_{alpha},;y_{alpha})), то через соответствующий ей угол ее координаты можно переписать как ((cosalpha,;sinalpha)).
Определение: 1. Синусом угла (alpha) называется ордината точки (P_{alpha}), соответствующей этому углу, на единичной окружности.
2. Косинусом угла (alpha) называется абсцисса точки (P_{alpha}), соответствующей этому углу, на единичной окружности.
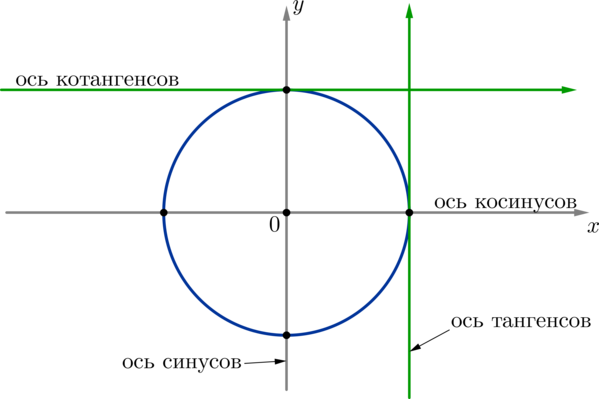
Поэтому ось (Oy) называют осью синусов, ось (Ox) — осью косинусов.
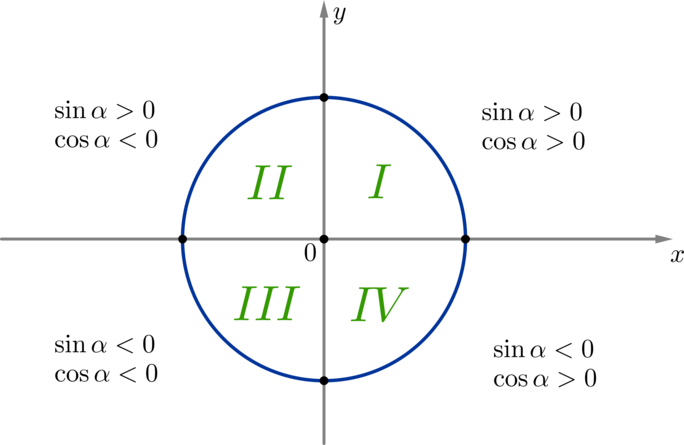
(blacktriangleright) Окружность можно разбить на (4) четверти, как показано на рисунке.
Т.к. в (I) четверти и абсциссы, и ординаты всех точек положительны, то косинусы и синусы всех углов из этой четверти также положительны.
Т.к. во (II) четверти ординаты всех точек положительны, а абсциссы — отрицательны, то косинусы всех углов из этой четверти — отрицательны, синусы — положительны.
Аналогично можно определить знак синуса и косинуса для оставшихся четвертей.
Пример 3. Так как, например, точки (P_{frac{pi}{6}}) и (P_{-frac{11pi}6}) совпадают, то их координаты равны, т.е. (sindfrac{pi}6=sin left(-dfrac{11pi}6right), cos
dfrac{pi}6=cos
left(-dfrac{11pi}6right)).
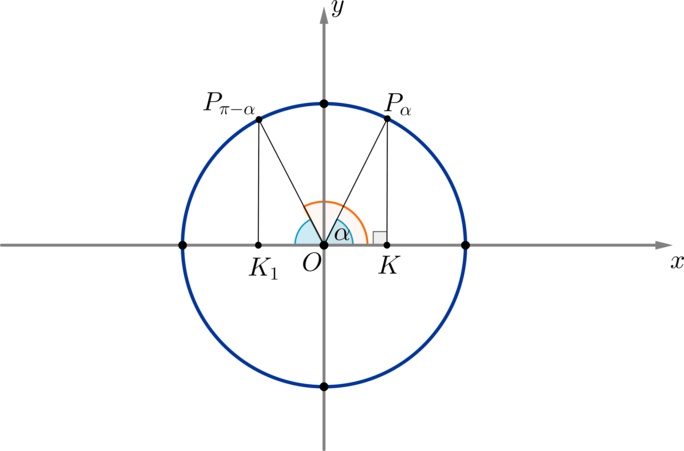
Пример 4. Рассмотрим точки (P_{alpha}) и (P_{pi-alpha}). Пусть для удобства (0<alpha<dfrac{pi}2).
Проведем перпендикуляры на ось (Ox): (OK) и (OK_1). Треугольники (OKP_{alpha}) и (OK_1P_{pi-alpha}) равны по гипотенузе и углу ((angle P_{alpha}OK=angle P_{pi-alpha}OK_1=alpha)).
Следовательно, (OK=OK_1, KP_{alpha}=K_1P_{pi-alpha}).
Т.к. координаты точки (P_{alpha}=(OK;KP_{alpha})=(cosalpha,;sinalpha)), а точки (P_{pi-alpha}=(-OK_1;K_1P_{pi-alpha})=(cos(pi-alpha),;sin(pi-alpha))), следовательно, [cos(pi-alpha)=-cosalpha, qquad sin(pi-alpha)=sinalpha]
Таким образом доказываются и другие формулы, называемые формулами приведения: [{large{begin{array}{l|r}
hline sin(pi-alpha)=sinalpha &
cos(pi-alpha)=-cosalpha\[2ex]
sin(pi+alpha)=-sinalpha &
cos(pi+alpha)=-cosalpha\[2ex]
sin(2pipmalpha)=pmsinalpha & cos
(2pipmalpha)=cosalpha\[2ex]
sin left(dfrac{pi}2pmalpharight)=cosalpha &
cosleft(dfrac{pi}2pmalpharight)=pmsinalpha\[2ex]
hline
end{array}}}]
С помощью этих формул можно найти синус или косинус любого угла, сведя это значение к синусу или косинусу угла из (I) четверти.
Таблица синусов, косинусов, тангенсов и котангенсов углов из первой четверти:
[{large{begin{array}{|c|c|c|c|c|c|}
hline &&&&&\[-17pt]
& quad 0 quad (0^ circ)& quad dfrac{pi}6 quad (30^circ)
& quad dfrac{pi}4
quad (45^circ) & quad dfrac{pi}3 quad (60^circ)& quad dfrac{pi}2 quad
(90^circ) \
&&&&&\[-17pt]
hline sin & 0 ½&frac{sqrt2}2&frac{sqrt3}2&1\[4pt]
hline cos &1&frac{sqrt3}2&frac{sqrt2}2½&0\[4pt]
hline mathrm{tg} &0 &frac{sqrt3}3&1&sqrt3&infty\[4pt]
hline mathrm{ctg} &infty &sqrt3&1&frac{sqrt3}3&0\[4pt]
hline
end{array}}}]
Заметим, что данные значения были выведены в разделе “Геометрия на плоскости (планиметрия). Часть II” в теме “Начальные сведения о синусе, косинусе, тангенсе и котангенсе”.
Пример 5. Найдите (sin{dfrac{3pi}4}).
Преобразуем угол: (dfrac{3pi}4=dfrac{4pi-pi}{4}=pi-dfrac{pi}4)
Таким образом, (sin{dfrac{3pi}4}=sinleft(pi-dfrac{pi}4right)=sindfrac{pi}4=dfrac{sqrt2}2).
(blacktriangleright) Для упрощения запоминания и использования формул приведения можно следовать следующему правилу.
Случай 1. Если угол можно представить в виде (ncdot pipm
alpha), где (ninmathbb{N}), то [sin(ncdot pipm
alpha)=bigodot sinalpha] где на месте (bigodot) стоит знак синуса угла (ncdot pipm alpha). [cos(ncdot pipm
alpha)=bigodot cosalpha] где на месте (bigodot) стоит знак косинуса угла (ncdot pipm alpha).
Знак угла можно найти, определив, в какой четверти он находится. Пользуясь таким правилом, предполагаем, что угол (alpha) находится в (I) четверти.
Случай 2. Если угол можно представить в виде (ncdot
pi+dfrac{pi}2pmalpha), где (ninmathbb{N}), то [sin(ncdot pi+dfrac{pi}2pm
alpha)=bigodot cosalpha] где на месте (bigodot) стоит знак синуса угла (ncdot pipm alpha). [cos(ncdot pi+dfrac{pi}2pm
alpha)=bigodot sinalpha] где на месте (bigodot) стоит знак косинуса угла (ncdot pipm alpha).
Знак определяется таким же образом, как и в случае (1).
Заметим, что в первом случае функция остается неизменной, а во втором случае — меняется (говорят, что функция меняется на кофункцию).
Пример 6. Найти (sin dfrac{13pi}{3}).
Преобразуем угол: (dfrac{13pi}{3}=dfrac{12pi+pi}{3}=4pi+dfrac{pi}3), следовательно, (sin dfrac{13pi}{3}=sin
left(4pi+dfrac{pi}3right)=sindfrac{pi}3=dfrac{sqrt3}2)
Пример 7. Найти (cos dfrac{17pi}{6}).
Преобразуем угол: (dfrac{17pi}{6}=dfrac{18pi-pi}{6}=3pi-dfrac{pi}6), следовательно, (cos dfrac{17pi}{6}=cos
left(3pi-dfrac{pi}6right)=-cosdfrac{pi}6=-dfrac{sqrt3}2)
(blacktriangleright) Область значений синуса и косинуса.
Т.к. координаты (x_{alpha}) и (y_{alpha}) любой точки (P_{alpha}) на единичной окружности находятся в пределах от (-1) до (1), а (cosalpha) и (sinalpha) — абсцисса и ордината соответственно этой точки, то [{large{-1leq cosalphaleq 1 ,qquad -1leqsinalphaleq 1}}]
Из прямоугольного треугольника по теореме Пифагора имеем: (x^2_{alpha}+y^2_{alpha}=1^2)
Т.к. (x_{alpha}=cosalpha, y_{alpha}=sinalpha Rightarrow) [{large{sin^2alpha+cos^2alpha=1}} — textbf{основное тригонометрическое тождество (ОТТ)}]
(blacktriangleright) Тангенс и котангенс.
Т.к. (mathrm{tg},alpha=dfrac{sinalpha}{cosalpha}, cosalphane 0)
(mathrm{ctg},alpha=dfrac{cosalpha}{sinalpha}, sinalphane 0), то:
1) ({large{mathrm{tg},alphacdot mathrm{ctg},alpha=1, cosalphane 0, sinalpha ne 0}})
2) тангенс и котангенс положительны в (I) и (III) четвертях и отрицательны в (II) и (IV) четвертях.
3) область значений тангенса и котангенса — все вещественные числа, т.е. (mathrm{tg},alphainmathbb{R},
mathrm{ctg},alphainmathbb{R})
4) для тангенса и котангенса также определены формулы приведения.
Случай 1. Если угол можно представить в виде (ncdot pipm
alpha), где (ninmathbb{N}), то [mathrm{tg},(ncdot pipm
alpha)=bigodot mathrm{tg},alpha] где на месте (bigodot) стоит знак тангенса угла (ncdot pipm alpha) ((cosalphane 0)). [mathrm{ctg},(ncdot pipm
alpha)=bigodot mathrm{ctg},alpha] где на месте (bigodot) стоит знак котангенса угла (ncdot pipm alpha) ((sinalphane 0)).
Случай 2. Если угол можно представить в виде (ncdot
pi+dfrac{pi}2pmalpha), где (ninmathbb{N}), то [mathrm{tg},(ncdot pi+dfrac{pi}2pm
alpha)=bigodot mathrm{ctg},alpha] где на месте (bigodot) стоит знак тангенса угла (ncdot pipm alpha) ((sinalphane 0)). [mathrm{ctg},(ncdot pi+dfrac{pi}2pm
alpha)=bigodot mathrm{tg},alpha] где на месте (bigodot) стоит знак котангенса угла (ncdot pipm alpha) ((cosalphane 0)).
5) ось тангенсов проходит через точку ((1;0)) параллельно оси синусов, причем положительное направление оси тангенсов совпадает с положительным направлением оси синусов;
ось котангенсов — через точку ((0;1)) параллельно оси косинусов, причем положительное направление оси котангенсов совпадает с положительным направлением оси косинусов.
Доказательство этого факта приведем на примере оси тангенсов.
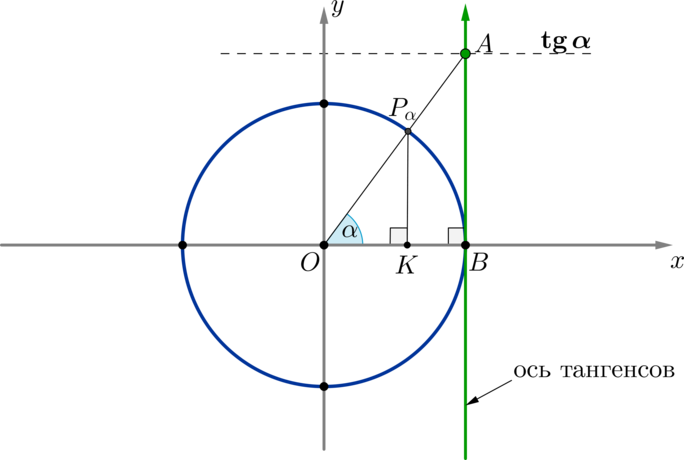
(triangle OP_{alpha}K sim triangle AOB Rightarrow
dfrac{P_{alpha}K}{OK}=dfrac{BA}{OB} Rightarrow
dfrac{sinalpha}{cosalpha}=dfrac{BA}1 Rightarrow
BA=mathrm{tg},alpha).
Таким образом, если точку (P_{alpha}) соединить прямой с центром окружности, то эта прямая пересечет линию тангенсов в точке, значение которой равно (mathrm{tg},alpha).
6) из основного тригонометрического тождества вытекают следующие формулы: [1+mathrm{tg},^2alpha=dfrac1{cos^2alpha},cosalphane 0 qquad qquad 1+mathrm{ctg},^2alpha=dfrac1{sin^2alpha}, sinalphane 0] Первую формулу получают делением правой и левой частей ОТТ на (cos^2alpha), вторую — делением на (sin^2alpha).
Обращаем внимание, что тангенс не определен в углах, где косинус равен нулю (это (alpha=dfrac{pi}2+pi n, ninmathbb{Z}));
котангенс не определен в углах, где синус равен нулю (это (alpha=pi+pi n, ninmathbb{Z})).
(blacktriangleright) Четность косинуса и нечетность синуса, тангенса, котангенса.
Напомним, что функция (f(x)) называется четной, если (f(-x)=f(x)).
Функция называется нечетной, если (f(-x)=-f(x)).
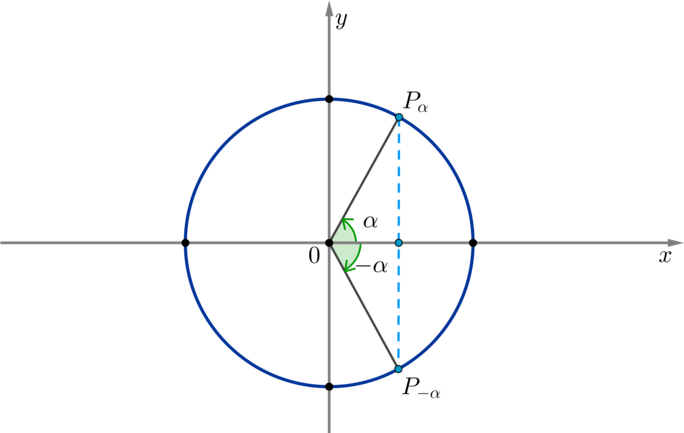
По окружности видно, что косинус угла (alpha) равен косинусу угла (-alpha) при любых значениях (alpha):
Таким образом, косинус — четная функция, значит, верна формула [{Large{cos(-x)=cos x}}]
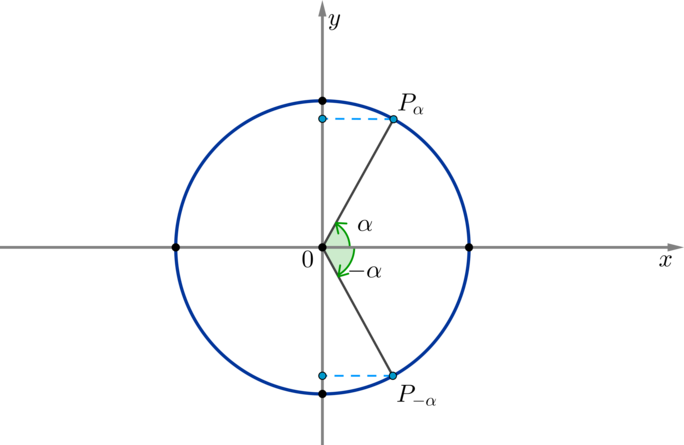
По окружности видно, что синус угла (alpha) противоположен синусу угла (-alpha) при любых значениях (alpha):
Таким образом, синус — нечетная функция, значит, верна формула [{Large{sin(-x)=-sin x}}]
Тангенс и котангенс также нечетные функции: [{Large{mathrm{tg},(-x)=-mathrm{tg},x}}] [{Large{mathrm{ctg},(-x)=-mathrm{ctg},x}}]
Т.к. (mathrm{tg},(-x)=dfrac{sin (-x)}{cos(-x)}=dfrac{-sin
x}{cos x}=-mathrm{tg},x qquad mathrm{ctg},(-x)=dfrac{cos(-x)}{sin(-x)}=-mathrm{ctg},x))