Описание презентации по отдельным слайдам:
-
1 слайд
Тригонометрия на ЕГЭ
Учитель математики:
Гореликова Инна Геннадьевна -
2 слайд
с
b
atg β =
ctg β =
Определение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника -
3 слайд
M(x;y)
ttg t =
ctg t =
Тригонометрические функции числового аргумента
у
х
R = 1 -
4 слайд
у
-1
1
1
-1
30°
60
90°
0° 360°
180°
270°
45°
Положительные углы
Отрицательные углы
— 30°
— 45°
— 60°
150°
135°
120°
— 90°
— 120°
— 135°
— 150°
y
x -
5 слайд
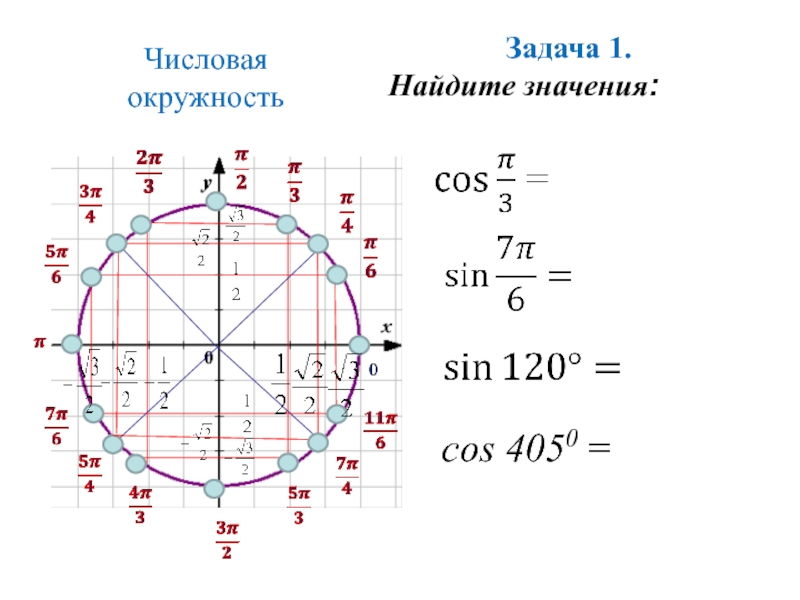
Задача 1.
Найдите значения:
Числовая окружность
cos 4050 = -
6 слайд
Тангенс и котангенс
Найдите ошибку:
-
7 слайд
Знаки тригонометрических функций
по координатным четвертям
сtg t
Основные тригонометрические формулы
1. sin² t + cos² t = 1
tg t
sin t
сos t
11. sin2t = 2 sin t·cos t
12. cos2t = cos² t — sin² t=
= 1 – 2sin² t =
= 2cos² t – 1 -
8 слайд
Решение:
Ответ:
Из основного тригонометрического
тождества находим значение sin α
с учетом его знака в данной
четверти.
2. Из тригонометрической
формулы тангенса находим tg α -
9 слайд
Формулы приведения
1) Определить четверть
2) Определить знак исходной функции в этой четверти0
Задача 3. Упростите выражение:tg (180° + t) =
ctg (90° — t) =
— sin t
-sin t
tg t
tg t -
10 слайд
Задача 4. Вычислите значение выражения:
Решение:
Ответ: -
11 слайд
Задача 5. Найдите значение выражения:
Решение:
Ответ:Так как tgt = 7, то … · 7 = …
-
12 слайд
Задача 6. Найдите значение выражения:
Решение:
Ответ: -
13 слайд
Задача 7. Найдите значение выражения:
Решение:
Ответ: -
-
15 слайд
Домашнее задание:
Спасибо за урок! -
16 слайд
Решение:
Ответ:Задача 9. Найдите значение выражения:
-
17 слайд
Задача 10. Найдите значение выражения:
Решение:
Ответ:
Краткое описание документа:
Данная презентация содержит слайды на повторение тригонометрии для учащихся 11 класса с целью успешной подготовки к ЕГЭ.
Данная презентация использовалась учителем при проведении дстанционного урока, организованного для учащихся десяти школ.
В ходе урока учащиеся имеют возможность повторить определения тригонометрических функций числового аргумента, основные тригонометрические формулы, формулы приведения.
В презентации приведены задания из ЕГЭ по данным темам,
4
Презентация к уроку-практикуму «Тригонометрия»
Презентация к уроку — практикуму по теме «Тригонометрия», ЕГЭ, профильный уровень, задание №9. Презентацию можно использовать на уроках повторения, систематизации знаний при подготовке к ЕГЭ по математике. В презентации рассмотрены задачи по тригонометрии (преобразование числовых и буквенных выражений) из открытого банка заданий ЕГЭ по математике (сайт ФИПИ). В конце представлен тест для проверки знаний по теме.
Опубликовано 30.04.17 в 21:37 в группе «Математика — это интересно!»
1.
Ох уж, эта
тригонометрия!
(Подготовка к ЕГЭ
по математике)
2.
Полезные советы при решении части 1
1
Прочитайте условие задачи. Если уверены, что умеете решать её – делайте
это сразу, если же есть сомнение, то переходите к следующей.
2
Решайте задачу не торопясь – обидно получить 0 баллов по
невнимательности или из-за описки.
3
Особое внимание уделите проверке выполнения арифметических
действий.
4
Если после второго прохода остались «белые пятна», не заполняйте их
«наугад». Постарайтесь вернуться к ним в конце всей работы.
5
Если вам кажется, что вопрос слишком прост, не ищите подвоха –
части 1 есть действительно простые вопросы.
6
В задачах части 1 полученный ответ часто можно проверить, подставив его
в исходную задачу, – сделайте это, если такая возможность есть.
7
На экзамене отсутствует справочный материал, поэтому постарайтесь
вспомнить (вывести) необходимые формулы и т.д.
в
3.
Полезные советы при решении части 2
1
После выполнения заданий части 1 сделайте небольшой перерыв,
отвлекитесь, а затем снова настройтесь на спокойную и вдумчивую работу.
2
Приготовьтесь к тому, что задачи этой части имеют «подводные камни».
3
Не забывайте о краткости записи решения при «полном» обосновании.
4.
Тригонометрия
5.
В чём ошибка?
cos x = 0,2, x = arccos 0,2 + 2Пn,
sin x = 0,2, x = (-1)ᵏarcsin 0,2 + Пn.
!!!
6.
!
!!
По мнению многих учеников, запись «n € Z» — избыточная.
В записи с использованием символа «±» теряется идея двух
серий решений тригонометрического уравнения.
7.
!!!
В формуле корней простейшего тригонометрического
уравнения sin t = a теряются идеи как двух серий решений
тригонометрического уравнения, так и периодичность
функции синус.
8.
Учимся решать!
9.
Тригонометрия на ЕГЭ
Решите уравнение
Задания В5
.
В ответе напишите наибольший отрицательный корень.
10.
Тригонометрия на ЕГЭ
Найдите значение выражения
Задания В7
.
11.
Тригонометрия на ЕГЭ
Найдите
Задания В7
12.
Тригонометрия на ЕГЭ
Задания В12
Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по
закону
, где t — время в секундах. Кинетическая энергия
груза, измеряемая в джоулях, вычисляется по формуле
,
где m — масса груза (в кг), v — скорость груза (в м/с). Определите, какую
долю времени из первой секунды после начала движения кинетическая
энергия груза будет не менее
Дж. Ответ выразите десятичной
дробью, если нужно, округлите до сотых.
13.
14.
Тригонометрия на ЕГЭ
Найдите точку минимума функции
,
принадлежащую промежутку
у’
у
.
0
Задания В14
—
0,5
+
15.
Тригонометрия на ЕГЭ
Найдите наибольшее значение функции
на отрезке
.
Задания В14
16.
Ура тестам!
17.
Найдите область определения выражения
При каких значениях х
имеет смысл выражения
.
.
18.
Укажите в каких
четвертях расположен ctg x , если
1и4
1и3
1и2
.
2и4
Укажите какие значения может принимать sin x ,
если у² = 4 sin x.
sin x > 0
sin x < 0
sin x 0
sin x 0
19.
Укажите какие значения может принимать tg x ,
если
.
tg x > 0
tg x < 0
tg x 0
tg x 0
Укажите в каких четвертях расположен cos x , если
3ʸ + 2cos x = 0.
1и4
1и2
2и3
3и4
20.
Хочу всё знать!
Задание С1
21.
Решить уравнение:
22.
Решите уравнение:
23.
Решите уравнение:
24.
25.
Чем мы хуже
МИОО?
26.
При каких значениях р имеет решения
уравнение 2 sin 2 x 2 p cos x 6 p 7 cos x 5
sin x 1
0.
Решение :
sin x 1 0, sin x 1, значит, sin x 1, cos х 0.
2 cos 2 x (2 p 7) cos x (6 p 3) 0,
cos x t , 1 t 1, 2t 2 ( 2 p 7)t (6 p 3) 0,
D (2 p 5) 2 0 при p R,
t1 p 0,5, t 2 3 не удовлетворяет 1 t 1.
1 p 0,5 1, 1,5 р 0,5,
Значит,
p 0,5 0;
р 0,5.
Ответ : р 1,5; 0,5) ( 0,5; 0, 5 .
27.
Всемирная паутина
на службе у ЕГЭ!
28.
http://avangard-school.nm.ru/
http://www.ctege.org/content/category/15/67/48/
http://rsr-olymp.ru/splash/
http://www.alleng.ru/edu/phys1.htm
http://alexlarin.narod.ru/ege.html
http://ege.stavedu.ru/
http://mathgia.ru:8080/or/gia12/
http://mathege.ru/or/ege/Main
http://shpargalkaege.ru/
http://pedsovet.su/
http://ege.do.am/news/shpargalka_dlja_ekzamena/2010-12-18-160
http://pedsovet.org/
http://www.openclass.ru/
http://1september.ru/
http://festival.1september.ru/
http://edu.1september.ru/
http://portfolio.1september.ru/
http://www.mcppomsk.ru/index.php?option=com_content&view=article&i
d=1&Itemid=1
http://le-savchen.ucoz.ru/
29.
Какое из данных уравнений не имеет
решений?
1) cos (2x – π) =
5
3
3) ctg x = 3;
Ответ: 4.
; 2) sin 0,3x
3
= 3 ;
10
4) 2sin x· cos x =
.
3
30.
Решите уравнение:
2 sin² x – sin x – 1 = 0.
2
2 n, n ; ( 1)
k
6
k , k
31.
Кот в мешке
Выберите среди данных уравнений однородное
уравнение первой степени и решите его:
1) сos x – sin 3x = 0;
2) cos x – 3sin x = 0;
3) cos x – 3sin x = 2;
4) cos² x – 3sin x = 0.
cos x – 3sin x = 0
32.
Решите уравнение:
4sin² x + 5 sin x cos x + cos² x = 0.
1
x n, n ; x arctg k , k
4
4
33.
Даны неравенства:
cos x >0, sin x 0,
sin x -0,5.
Укажите какое-либо число, удовлетворяющее
всем трём неравенствам одновременно.
34.
Решите уравнение sin 2x – 3 cos x = 0.
2 sin x cos x 3 cos x 0,
cos x (2 sin x 3) 0,
cos x 0
x
2
или
n, n
2 sin x 3 0,
sin x 1,5 решений нет.
Ответ :
2
n, n .
35.
Найдите наименьший корень уравнения
2cos² x = 1 + sin x.
2(1 sin 2 x) 1 sin x,
2 sin 2 x sin x 1 0,
sin x 1
1
sin x ,
2
или
Наименьший положительный корень х .
6
36. При каких значениях х значения функции равно 0?
При каких значениях х значения функции
x
x
f ( x) 4 sin cos 1
2
2
равно 0?
x
x
1
4 sin cos 1 0, 2 sin x 1, sin x ,
2
2
2
x ( 1)
k
6
k , k
37.
Выберите уравнение, которое имеет решение,
показанное на единичной окружности:
1) tg x = 1;
2) sin x = 0;
1
3) сos x = 2 ;
3
4) sin x =
.
2
38.
Вопрос от учителя
Какая ошибка допущена в решении уравнения?
tg ( 2 x
2x
2x
x
4
3
24
4
) 3,
arctg 3 n, n ,
4
n, n ,
2 n, n .
39.
Аукцион
Укажите на тригонометрической окружности все точки,
удовлетворяющие неравенству: sin x > 0,5.
40.
Какой корень уравнения
х
cos = 1 принадлежит отрезку [ -π; π]?
2
х=0
41.
При каких значениях а уравнение
sin² x – (a + 3) sin x + 3a = 0
не имеет решений?
2
Пусть sin x t , t 1. t (a 3) t 3a 0.
D (a 3) 0 при а R, t1 3, t 2 a.
2
Значит, уравнение не будет иметь корней
при а ( ; 1) (1; ).
42.
Кот в мешке
Найдите значения х, при которых график функции
у 2 cos х 1 лежит выше оси х.
2 cos х 1 0, cos x
1
2
,
4
2 n x
4
2 n, n
43.
Как, не решая уравнения ctg 2 x 1
1
sin 2 x
,
определить, какая серия является решением?
1)
2
n, n
3) n, n
1)
2) 2 n, n
4)
n
2
, n
44.
Найдите все х, обращающие в нуль произведение
2
функций у cos x
2
и
у sin 4 x .
2
cos x
sin 4 x 0,
2
cos x
2
2
или
sin 4 x 0
4 x n, n
x
n
4
, n
45.
Вопрос от учителя
Решите неоднородное уравнение второй степени
2sin² x – 5 sin x cos x + 5 cos² x = 1.
2 sin 2 x 5 sin x cos x 5 cos 2 x sin 2 x cos 2 x,
sin 2 x 5 sin x cos x 4 cos 2 x 0, разделим на cos 2 x,
tg 2 x 5 tg x 4 0,
tg x 1
x
4
n, n
или
tg x 4
x arctg 4 m, m
46.
Решите уравнение sin² x + cos 2x = b, если
одно из его решений
6
.
2 1 1 3
b sin
cos
.
6
6 4 2 4
3 1 cos 2 x
3
2
sin x cos 2 x ,
cos 2 x ,
4
2
4
2
2 2 cos 2 x 4 cos 2 x 3,
2x
3
2 n, n , x
6
1
2 cos 2 x 1, cos 2 x ,
2
n, n
47.
Решите уравнение cos x + sin x = cos 3x.
(cos 3 x cos x) sin x 0,
2 sin 2 x sin x sin x 0,
sin x ( 2 sin 2 x 1) 0,
sin x 0
x n, n
или
1
sin 2 x
2
2 x ( 1)
x ( 1)
k 1
k 1
6
12
k , k ,
k
2
, k
48.
Решите уравнение
2 sin x 2 0,
2 cos 2 0;
2 sin x 2
2 cos 2
sin x
cos x
x 2 n, n
4
2
,
2
2
2
0 .
49.
СУПЕРИГРА
Решите уравнение 1 tg x x
2
1 tg 2 x x 2 4 x 2 ,
2 x 2
2
3
n 2
6
6
n
3
3
n 0, x
3
2
tg 2 x 3,
2 x 2
2
3
4 x
x
n, n ,
3
2 x 2
n 2
6
6
n
3
3
n 0, x
2
3
2
.
50. М о л о д ц ы ! ! !
Молодцы!!!
«Скажи мне, и я забуду,
Покажи мне, и я запомню,
Вовлеки меня, и я научусь».
(Китайская пословица)
Математика, уже давно стала языком науки и техники, и в настоящее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется, казалось бы, в традиционно далекие от нее области. Интенсивная математизация различных областей человеческой деятельности особенно усилилась со стремительным развитием ЭВМ. Компьютеризация общества, внедрение современных информационных технологий требуют математической грамотности человека на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления. В частности, важным аспектом является изучение тригонометрии. Учение о тригонометрических функциях имеет широкое применение в практике, при изучении множества физических процессов, в промышленности, и даже в медицине. Учащихся, которые в дальнейшем в своей профессиональной деятельности будут пользоваться математикой, необходимо обеспечить высокой математической подготовкой.
Тригонометрия – составная часть школьного курса математики. Хорошие знания и прочные навыки по тригонометрии являются свидетельством достаточного уровня математической культуры, непременным условием успешного изучения в вузе математики, физики, ряда технических дисциплин. Однако значительная часть выпускников школ обнаруживает из года в год весьма слабую подготовку по этому важному разделу математики, о чём свидетельствуют результаты прошлых лет, так как анализ сдачи единого государственного экзамена показал, что ученики допускают много ошибок при выполнении заданий именно этого раздела или вообще не берутся за такие задания.
А ведь еще греки, на заре человечества, считали тригонометрию важнейшей из наук, ибо геометрия — царица математики, а тригонометрия — царица геометрии. Поэтому и мы, не оспаривая древних греков, будем считать тригонометрию одним из важнейших разделов школьного курса, да и всей математической науки в целом.
Физика и геометрия не обходятся без тригонометрии. Не обходится без тригонометрии и Единый государственный экзамен. Только в части В вопросы по тригонометрии встречаются почти в трети видов заданий. Это и решение простейших тригонометрических уравнений в задании В5, и работа с тригонометрическими выражениями в задании В7, и исследование тригонометрических функций в задании В14, а так же задания В12, в которых имеются формулы, описывающие физические явления и содержащие тригонометрические функции. Нельзя не отметить и геометрические задания, в решении которых используются и определения синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника, и основные тригонометрические тождества. И это – только часть В! А ведь ещё есть и любимые тригонометрические уравнения с отбором корней С1, и «не очень любимые» геометрические задания С2 и С4.
Как провести подготовку учащихся по этим темам? Способов можно предложить большое количество, но самое главное, чтобы у ребят не возникало чувство страха и ненужного волнения, в связи с огромным разнообразием различных заданий и формул. А для этого необходимо создания позитивного настроения при решении этих заданий. Данная презентация может быть использована и для проведения занятий с учащимися, и для выступлений на семинарах математиков по подготовке к ЕГЭ. В ней предложены некоторые виды заданий и разобраны их решения.
Хорошим тренингом может являться не только простое решение уже данных заданий, но и самостоятельное составление их учащимися. В зависимости от подготовки, это могут быть и тесты на отработку ограничений в решении тригонометрических уравнений С1, и даже сами уравнения.
Другим активным методом является проведение занятий в форме интеллектуальных игр. Одним из самых удобных вариантов, я считаю, формат «Своей игры». Эту игровую форму, особенно сейчас с использованием компьютерных презентаций, можно применить и при зачетных уроках, после изучения тем, и при подготовке к ЕГЭ. В предложенной работе размещена «Своя игра. Решение тригонометрических уравнений и неравенств».
Результатом предложенной работы должно быть успешное решение заданий ЕГЭ по теме «Тригонометрия».
Слайд 1
Решение тригонометрических уравнений С1 Балагурова-Шемота Н.Ю лицей №90
Слайд 2
До экзамена осталось 160 дней лицей №90 Балагурова-Шемота Н.Ю. 2
Слайд 3
Повторим лицей №90 Балагурова-Шемота Н.Ю. 3
Слайд 4
Повторим лицей №90 Балагурова-Шемота Н.Ю. 4
Слайд 5
лицей №90 Балагурова-Шемота Н.Ю. 5
Слайд 6
лицей №90 Балагурова-Шемота Н.Ю. 6 sin α = №0 Мизинец 0 0 №1 Безымянный 30 0 №2 Средний 45 0 №3 Указательный 60 0 №4 Большой 90 0
Слайд 7
лицей №90 Балагурова-Шемота Н.Ю. 7
Слайд 8
лицей №90 Балагурова-Шемота Н.Ю. 8
Слайд 9
Отбор корней лицей №90 Балагурова-Шемота Н.Ю. 9
Слайд 10
Найти ошибку лицей №90 Балагурова-Шемота Н.Ю. 10
Слайд 11
лицей №90 Балагурова-Шемота Н.Ю. 11
Слайд 12
лицей №90 Балагурова-Шемота Н.Ю. 12
Слайд 13
лицей №90 Балагурова-Шемота Н.Ю. 13
Слайд 14
Ответ: лицей №90 Балагурова-Шемота Н.Ю. 14
Слайд 15
лицей №90 Балагурова-Шемота Н.Ю. 15
Слайд 16
лицей №90 Балагурова-Шемота Н.Ю. 16
Слайд 17
лицей №90 Балагурова-Шемота Н.Ю. 17 , и .
Слайд 18
Ответ: лицей №90 Балагурова-Шемота Н.Ю. 18
Слайд 19
лицей №90 Балагурова-Шемота Н.Ю. 19
Слайд 20
лицей №90 Балагурова-Шемота Н.Ю. 20
Слайд 21
лицей №90 Балагурова-Шемота Н.Ю. 21
Слайд 22
НАЙТИ ОШИБКУ лицей №90 Балагурова-Шемота Н.Ю. 22
Слайд 23
http://mathege.ru/or/ege/Main Открытый банк заданий http://uztest.ru/exam?idexam=30 http :// egeurok . ru / generators / ege _ matem _2014/ generator _ variantov _ ege _ matem _2014. html Генератор вариантов http://alexlarin.net/ege14.html Ларин Александр Александрович http://reshuege.ru/ лицей №90 Балагурова-Шемота Н.Ю. 23
Слайд 24
Повтори лицей №90 Балагурова-Шемота Н.Ю. 24
Тригонометрия(В5, В7)
на ЕГЭ.
Подготовка к ЕГЭ 10 класс
Составитель:
учитель математики МОУ СОШ №203 ХЭЦ
г. Новосибирск
Видутова Т. В
Задание B5 (№ 12895)
Найдите корень уравнения
В ответе запишите наибольший отрицательный корень.
1
Задание B5 (№ 104023)
Найдите корень уравнения .
В ответе напишите наименьший положительный корень.
2
Задание B5 (№ 103513)
Найдите корень уравнения .
В ответе напишите наибольший отрицательный корень.
3
Задание B7 (№ 17293)
Найдите значение выражения:
4
Задание B7 (№ 26941)
Найдите значение выражения: .
5
6
Задание B7 (№ 26943)
Найдите значение выражения: .
Задание B7 (№ 26949)
Найдите значение выражения: .
7
8
Задание B7 (№ 26951)
Найдите значение выражения: .
9
Задание B7 (№ 26955)
Найдите , если и .
Задание B7 (№ 26959)
Найдите значение выражения : .
10
11
Задание B7 (№ 26961)
Найдите значение выражения ,
если .
Задание B7 (№ 26965)
Найдите , если .
12
Задание B7 (№ 26967)
Найдите , если .
13
14
Задание B7 (№ 26971)
Найдите значение выражения ,
если .
Самостоятельная работа 1 вариант 2 вариант
- Найдите наибольший
отрицательный корень
- Найдите наименьший
положительный корень
- Найдите значение выражения
- Найдите ,
если .
1. Найдите наименьший положительный корень
2. Найдите наибольший
отрицательный корень
- Найдите значение выражения
- Найдите ,
если .
Задание B5 (№ 13043)
Найдите корень уравнения
В ответе запишите наибольший отрицательный корень.
4
Задание B5 (№ 13229)
Найдите корень уравнения
В ответе запишите наибольший отрицательный корень.
5
6
Задание B5 (№ 104015)
Найдите корень уравнения .
В ответе напишите наименьший положительный корень.
Задание B5 (№ 103745)
Найдите корень уравнения .
В ответе напишите наибольший отрицательный корень.
7
.
Задание B5 (№ 103501)
Найдите корень уравнения .
В ответе напишите наибольший отрицательный корень.
8
Задание B5 (№ 103463)
Найдите корень уравнения .
В ответе напишите наименьший положительный корень.
9
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Тригонометрия на ЕГЭ
Содержание
-
1.
Презентация по математике на тему Тригонометрия на ЕГЭ -
2.
сba tg β =ctg β =Определение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника -
3.
M(x;y)t tg t =ctg t =Тригонометрические функции числового аргументаухR = 1 -
4.
30°6090°0° 360°180°270°45°Положительные углыОтрицательные углы- 30°- 45°- 60°- 90°yx -
5.
Задача 1. Найдите значения:Числовая окружностьcos 4050 = -
6.
Тангенс и котангенс -
7.
Знаки тригонометрических функцийпо координатным четвертямсtg tОсновные тригонометрические -
8.
Решение:Ответ:Из основного тригонометрического тождества -
9.
Формулы приведения1) Определить четверть2) Определить знак исходной -
10.
Задача 4. Вычислите значение выражения: Решение:Ответ: -
11.
Задача 5. Найдите значение выражения: Решение:Ответ: Так как -
12.
Задача 6. Найдите значение выражения: Решение:Ответ: -
13.
Задача 7. Найдите значение выражения: Решение:Ответ: -
14.
Решение:Ответ: -
15.
Домашнее задание:Спасибо за урок! -
16.
Решение:Ответ:Задача 9. Найдите значение выражения: -
17.
Задача 10. Найдите значение выражения: Решение:Ответ:
сba tg β =ctg β =Определение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника
Слайд 1Тригонометрия на ЕГЭ
Учитель математики:
Гореликова Инна Геннадьевна

Слайд 2
с
b
a
tg β =
ctg β =
Определение синуса, косинуса, тангенса и котангенса острого
угла прямоугольного треугольника

Слайд 3
M(x;y)
t
tg t =
ctg t =
Тригонометрические функции числового аргумента
у
х
R = 1

Слайд 4
30°
60
90°
0° 360°
180°
270°
45°
Положительные углы
Отрицательные углы
— 30°
— 45°
— 60°
— 90°
y
x

Слайд 5
Задача 1.
Найдите значения:
Числовая окружность
cos 4050 =
Слайд 7Знаки тригонометрических функций
по координатным четвертям
сtg t
Основные тригонометрические формулы
1. sin² t +
cos² t = 1
tg t
sin t
сos t
11. sin2t = 2 sin t·cos t
12. cos2t = cos² t — sin² t=
= 1 – 2sin² t =
= 2cos² t – 1

Слайд 8Решение:
Ответ:
Из основного тригонометрического
тождества находим значение sin α
с учетом его знака в данной
четверти.
2. Из тригонометрической
формулы тангенса находим tg α

Слайд 9Формулы приведения
1) Определить четверть
2) Определить знак исходной функции в этой четверти
0
Задача
3. Упростите выражение:
tg (180° + t) =
ctg (90° — t) =
— sin t
-sin t
tg t
tg t

Слайд 10Задача 4. Вычислите значение выражения:
Решение:
Ответ:

Слайд 11
Задача 5. Найдите значение выражения:
Решение:
Ответ:
Так как tgt = 7, то
… · 7 = …

Слайд 12Задача 6. Найдите значение выражения:
Решение:
Ответ:

Слайд 13Задача 7. Найдите значение выражения:
Решение:
Ответ:

Слайд 15Домашнее задание:
Спасибо за урок!

Слайд 16Решение:
Ответ:
Задача 9. Найдите значение выражения:

Слайд 17Задача 10. Найдите значение выражения:
Решение:
Ответ:


























