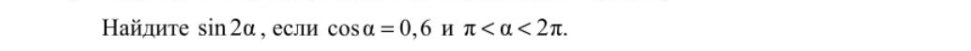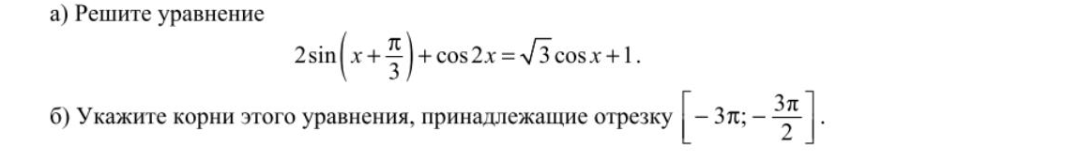СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Тригонометрические уравнения
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Тип 12 № 507595
а) Решите уравнение
б) Найдите корни этого уравнения, принадлежащие промежутку
Аналоги к заданию № 507595: 500917 501709 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
2
Тип 12 № 510018
а) Решите уравнение
б) Укажите корни этого уравнения, принадлежащие промежутку
Источник: Демонстрационная версия ЕГЭ—2016 по математике. Профильный уровень.
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла, Формулы приведения
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
1 комментарий · Сообщить об ошибке · Помощь
3
Тип 12 № 504543
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 504543: 504564 507292 510671 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, решаемые разложением на множители
Методы алгебры: Группировка
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
2 комментария · Сообщить об ошибке · Помощь
4
Тип 12 № 500366
а) Решите уравнение
б) Найдите все корни этого уравнения, принадлежащие отрезку
Аналоги к заданию № 500366: 500587 501482 514505 Все
Классификатор алгебры: Тригонометрические уравнения
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
4 комментария · Сообщить об ошибке · Помощь
5
Тип 12 № 509579
а) Решите уравнение
б) Найдите все корни уравнения, принадлежащие отрезку
Аналоги к заданию № 509579: 509926 509947 509968 515762 519665 Все
Классификатор алгебры: Тригонометрические уравнения, Тригонометрические уравнения, сводимые к целым на синус или косинус
Методы алгебры: Формулы двойного угла
Кодификатор ФИПИ/Решу ЕГЭ: 2.1.4 Тригонометрические уравнения
Решение
·
·
Курс Д. Д. Гущина
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
Чуть больше 30% выпускников справляется с тригонометрией на ЕГЭ по математике. И неудивительно: для решения заданий из базы и профиля надо знать очень много формул, которые сложно освоить за 1-2 года. На самом деле, это миф! Чтобы решить задания по тригонометрии, нужно знать всего 5 формул — и просто уметь ими пользоваться.
Тригонометрия на ЕГЭ: основные проблемы темы
Чаще всего тригонометрию начинают изучать в 10 классе — но в некоторых школах оставляют до 11. В первом случае у учеников есть 2 года, чтобы освоить новую тему. А во втором, к сожалению, всего год. И это проблема. Дело в том, что в тригонометрии очень много формул, которые нужно знать, чтобы успешно решать задания. Если за 2 года их можно успеть выучить, то за год это будет сделать проблематично.
Ситуация осложняется ещё двумя факторами. Во-первых, в самой математике много формул, признаков, теорем и т.д. Во-вторых, кроме математики есть и другие экзамены, для которых нужно выучить большой объём информации.
Именно поэтому я всегда советую своим ученикам не учить формулы для тригонометрии на ЕГЭ, а выводить! Но об этом мы поговорим чуть позже, а сейчас давайте обсудим, почему тригонометрия так важна и где в ЕГЭ ее можно встретить.
Задания по тригонометрии в базе и профиле на ЕГЭ
Так как ЕГЭ по математике делится на базовый и профильный, а тригонометрия встречается в обоих, то давайте рассмотрим оба уровня экзамена.
Тригонометрия в базе
Что касается Базового уровня, то в нём всего 3 задания, в которых можно столкнуться с тригонометрией:
В № 7 в виде простейшего выражения
Как правило, для успешного решения таких заданий достаточно воспользоваться формулами из справочного материала.
В № 8 в виде формулы прикладной задачи
Стоит отметить, что в базовом ЕГЭ в прикладных задачах тригонометрия попадается редко, но нужно быть готовыми.
В № 15 как тригонометрия в геометрии
В справочном материале есть вся необходимая информация для успешного решения данного задания, а именно определение всех тригофункций в прямоугольном треугольнике.
Тригонометрия в профиле
Базовый уровень мы рассмотрели, теперь перейдём к профильному. Здесь уже больше вариантов, в которых можно встретиться с тригонометрией. Давайте посмотрим на Части 1 и 2.
В № 3 как тригонометрия в геометрии (Часть 1)
То же самое задание, как в базовом ЕГЭ, вот только в справочном материале уже нет необходимой информации.
В № 4 в виде выражения (Часть 1)
То же самое задание, как в базовом ЕГЭ.
В № 7 в виде формулы прикладной задачи (Часть 1)
То же самое задание, как в базовом ЕГЭ. Для успешного решения подойдут базовые навыки работы с тригонометрией.
В № 11 как часть функции (Часть 1)
Функцию нужно проанализировать для поиска наибольшего/наименьшего значения или точек максимума/минимума.
Если с Частью 1 профиля всё более-менее очевидно, то во второй части бывают сюрпризы, о которых ученики даже не подозревают. Да-да, тригонометрия на ЕГЭ умеет прятаться и в Части 2. Давайте посмотрим на эти задания.
В № 12 (Часть 2)
Тут сюрпризов нет. Это уравнение второй части, в котором ученики как раз ожидают увидеть тригонометрию, хотя она там бывает не всегда!
В № 13 — стереометрия (Часть 2)
Да, тригонометрия может встретиться здесь в виде теоремы синусов или теоремы косинусов, а ещё в виде формул в методе координат (для любителей решать этим методом).
В № 16 — планиметрия (Часть 2)
Здесь всё аналогично стереометрии: есть геометрические формулы, в которых прячется тригонометрия. Ведь, как я и сказала выше, в геометрии она тоже бывает!
5 формул тригонометрии: теория для ЕГЭ
А теперь предлагаю перейти к самому интересному — а именно к формулам. К сожалению, их действительно много. А ещё они похожи, и если их просто учить (или бездумно зубрить), то велик риск перепутать «+» с «–» или забыть какую-нибудь единичку.
Именно поэтому я рекомендую не учить формулы, а выводить. Это очень удобно тем более, что в профильном ЕГЭ по математике весь справочный материал состоит из 5-ти формул тригонометрии, из которых очень легко выводятся все остальные.
Но прежде чем я расскажу вам, как выводятся тригонометрические формулы, пообещайте, что обязательно отработаете все правила выведения! Для этого нужно будет регулярно выводить формулы по указанным ниже схемам.
Вот формулы, которые будут у вас в справочном материале:
Формула № 1 и как она пригодится в поиске котангенса и тангенса
Первая формула — основное тригонометрическое тождество (ОТТ):
Обычно ученики знают ее очень хорошо. Она связывает синус и косинус и помогает найти одну функцию через другую.
С этой формулой косвенно связана другая (ее нет в справочном материале), которая тоже легко дается школьникам:
Эту формулу очень легко запомнить, если знать, как можно расписать тангенс и котангенс через синус и косинус:
Эти 2 формулы связывают по отдельности синус с косинусом и тангенс с котангенсом. Но иногда требуется, чтобы были связаны все 4 функции, и здесь на помощь приходят следствия из ОТТ (как раз та самая формула № 1).
Чтобы вывести следствия нужно всего лишь разделить ОТТ на sin2 и cos2:
Теперь можно легко найти:
- котангенс, зная синус,
- или тангенс, зная косинус.
Формула № 2 и что из нее можно вывести
С тождествами разобрались, давайте перейдём к формулам двойного угла. Что касается синуса двойного угла (вторая формула в справочном материале):
Здесь всё просто, берёте и применяете формулу, если видите, что она нужна для задания.
Формула № 3 и что из нее можно вывести
А вот с косинусом двойного угла (третья формула в справочном материале) всё интереснее. Безусловно, косинус двойного угла:
в чистом виде встречается, и тогда вы делаете всё тоже самое, что с синусом. Но на самом деле есть ещё 2 формулы, которые очень просто вывести, используя ОТТ (формулу № 1). Для начала нужно выразить квадрат синуса и квадрат косинуса из ОТТ (Шаг 1):
А потом нужно подставить эти значения в формулу (6, или третья формула справочного материала) (Шаг 2):
Вот мы вывели ещё 2 формулы! А сейчас я покажу вам как практически ничего не делая получить ещё 2. Мы будем выводить формулы понижения степени из формул двойного угла. Смотрите, нужно всего лишь выразить одно из другого:
Формулы № 4 и 5 и что из них можно вывести
Давайте посмотрим на справочный материал, у нас там ещё целых 2 формулы, из которых мы получим конечно же ещё 2! Сейчас вообще ничего удивительного не будет. Вот формулы, которые уже даны:
Как вы заметили, они для суммы углов, а чтобы получить формулы для разности углов, нам нужно всего лишь поменять знаки в формуле на противоположные (разумеется, я говорю про «+» и «–»):
Вот так при помощи нехитрых преобразований из 5-ти формул справочного материала мы получили целых 14!
Все скриншоты взяты из открытого банка заданий ФИПИ или из демоверсий ЕГЭ по математике 2022.
Что еще пригодится вам для тригонометрии на ЕГЭ
Скажу по секрету, что это далеко не все формулы тригонометрии, которые существуют. Есть и другие:
- некоторые можно вывести из вышеуказанных,
- некоторые можно обобщить и вместо огромного количества формул использовать короткое правило.
Но мне кажется, что пока этого и так много!
Советую сначала хорошо отработать формулы, которые я перечислила в этой статье, и только потом браться за другие. Так вы не загрузите свою память и будете быстрее решать сложные задания по тригонометрии из ЕГЭ. Это, кстати, касается любой темы на экзамене по математике: а в ЕГЭ их очень много. Поэтому чтобы получить высокий балл, надо правильно и системно отработать их все.
Именно так я и строю подготовку к ЕГЭ по математике вместе со своими учениками: строгая система подготовки — ключ к успеху на экзамене. Сначала мы разбираем простые темы и задания и учимся решать их самыми удобными способами — почти на автомате. А после я добавляю более хитрые и сложные задания. В итоге ребята и имеют хорошую базу знаний по математике, и умеют решать самые разные типы задач. Так что если вы хотите по-настоящему знать математику, а не зазубривать формулы, приходите на мои уроки!
А чтобы отрабатывать выведение было не так скучно, держите моего котика, который любезно согласился позировать в позе котангенса:
Прототипы задания №1 профильного ЕГЭ 2022 по математике
Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.
Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.
Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы
| Источник: math100.ru | → Рациональные уравнения
→ Тригонометрические уравнения |
| time4math.ru | → скачать задания |
| vk.com/ekaterina_chekmareva | → задания |
При отработке данного задания будут полезны книги:
Задания по теме «Тригонометрические уравнения»
Открытый банк заданий по теме тригонометрические уравнения. Задания C1 из ЕГЭ по математике (профильный уровень)
Задание №1179
Условие
а) Решите уравнение 2(sin x-cos x)=tgx-1.
б) Укажите корни этого уравнения, принадлежащие промежутку left[ frac<3pi >2;,3pi right].
Решение
а) Раскрыв скобки и перенеся все слагаемые в левую часть, получим уравнение 1+2 sin x-2 cos x-tg x=0. Учитывая, что cos x neq 0, слагаемое 2 sin x можно заменить на 2 tg x cos x, получим уравнение 1+2 tg x cos x-2 cos x-tg x=0, которое способом группировки можно привести к виду (1-tg x)(1-2 cos x)=0.
1) 1-tg x=0, tg x=1, x=fracpi 4+pi n, n in mathbb Z;
2) 1-2 cos x=0, cos x=frac12, x=pm fracpi 3+2pi n, n in mathbb Z.
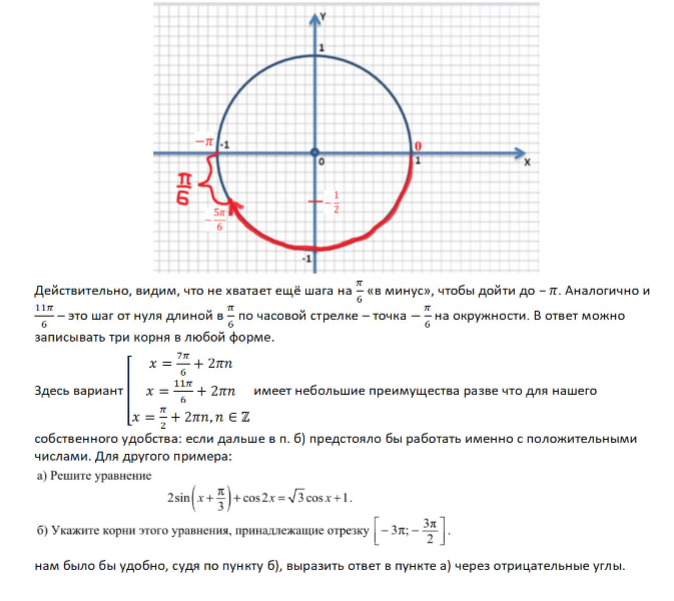
б) С помощью числовой окружности отберём корни, принадлежащие промежутку left[ frac<3pi >2;, 3pi right].
x_1=fracpi 4+2pi =frac<9pi >4,
x_2=fracpi 3+2pi =frac<7pi >3,
x_3=-fracpi 3+2pi =frac<5pi >3.
Ответ
а) fracpi 4+pi n, pmfracpi 3+2pi n, n in mathbb Z;
б) frac<5pi >3, frac<7pi >3, frac<9pi >4.
Задание №1178
Условие
а) Решите уравнение (2sin ^24x-3cos 4x)cdot sqrt =0.
б) Укажите корни этого уравнения, принадлежащие промежутку left( 0;,frac<3pi >2right] ;
Решение
а) ОДЗ: begin tgxgeqslant 0\xneq fracpi 2+pi k,k in mathbb Z. end
Исходное уравнение на ОДЗ равносильно совокупности уравнений
left[!!begin 2 sin ^2 4x-3 cos 4x=0,\tg x=0. endright.
Решим первое уравнение. Для этого сделаем замену cos 4x=t, t in [-1; 1]. Тогда sin^24x=1-t^2. Получим:
t_1=frac12, t_2=-2, t_2notin [-1; 1].
4x=pm fracpi 3+2pi n,
x=pm fracpi <12>+frac<pi n>2, n in mathbb Z.
Решим второе уравнение.
tg x=0,, x=pi k, k in mathbb Z.
При помощи единичной окружности найдём решения, которые удовлетворяют ОДЗ.
Знаком «+» отмечены 1 -я и 3 -я четверти, в которых tg x>0.
Получим: x=pi k, k in mathbb Z; x=fracpi <12>+pi n, n in mathbb Z; x=frac<5pi ><12>+pi m, m in mathbb Z.
б) Найдём корни, принадлежащие промежутку left( 0;,frac<3pi >2right].
Ответ
а) pi k, k in mathbb Z; fracpi <12>+pi n, n in mathbb Z; frac<5pi ><12>+pi m, m in mathbb Z.
Задание №1177
Условие
а) Решите уравнение: cos ^2x+cos ^2fracpi 6=cos ^22x+sin ^2fracpi 3;
б) Укажите все корни, принадлежащие промежутку left( frac<7pi >2;,frac<9pi >2right].
Решение
а) Так как sin fracpi 3=cos fracpi 6, то sin ^2fracpi 3=cos ^2fracpi 6, значит, заданное уравнение равносильно уравнению cos^2x=cos ^22x, которое, в свою очередь, равносильно уравнению cos^2x-cos ^2 2x=0.
Но cos ^2x-cos ^22x= (cos x-cos 2x)cdot (cos x+cos 2x) и
cos 2x=2 cos ^2 x-1, поэтому уравнение примет вид
(cos x-(2 cos ^2 x-1)),cdot (cos x+(2 cos ^2 x-1))=0,
(2 cos ^2 x-cos x-1),cdot (2 cos ^2 x+cos x-1)=0.
Тогда либо 2 cos ^2 x-cos x-1=0, либо 2 cos ^2 x+cos x-1=0.
Решая первое уравнение как квадратное уравнение относительно cos x, получаем:
(cos x)_<1,2>=frac<1pmsqrt 9>4=frac<1pm3>4. Поэтому либо cos x=1, либо cos x=-frac12. Если cos x=1, то x=2kpi , k in mathbb Z. Если cos x=-frac12, то x=pm frac<2pi >3+2spi , s in mathbb Z.
Аналогично, решая второе уравнение, получаем либо cos x=-1, либо cos x=frac12. Если cos x=-1, то корни x=pi +2mpi , m in mathbb Z. Если cos x=frac12, то x=pm fracpi 3+2npi , n in mathbb Z.
Объединим полученные решения:
x=mpi , m in mathbb Z; x=pm fracpi 3 +spi , s in mathbb Z.
б) Выберем корни, которые попали в заданный промежуток, с помощью числовой окружности.
Получим: x_1 =frac<11pi >3, x_2=4pi , x_3 =frac<13pi >3.
Ответ
а) mpi, m in mathbb Z; pm fracpi 3 +spi , s in mathbb Z;
б) frac<11pi >3, 4pi , frac<13pi >3.
Задание №1176
Условие
а) Решите уравнение 10cos ^2frac x2=frac<11+5ctgleft( dfrac<3pi >2-xright) ><1+tgx>.
б) Укажите корни этого уравнения, принадлежащие интервалу left( -2pi ; -frac<3pi >2right).
Решение
а) 1. Согласно формуле приведения, ctgleft( frac<3pi >2-xright) =tgx. Областью определения уравнения будут такие значения x , что cos x neq 0 и tg x neq -1. Преобразуем уравнение, пользуясь формулой косинуса двойного угла 2 cos ^2 frac x2=1+cos x. Получим уравнение: 5(1+cos x) =frac<11+5tgx><1+tgx>.
Заметим, что frac<11+5tgx><1+tgx>= frac<5(1+tgx)+6><1+tgx>= 5+frac<6><1+tgx>, поэтому уравнение принимает вид: 5+5 cos x=5 +frac<6><1+tgx>. Отсюда cos x =frac<dfrac65><1+tgx>, cos x+sin x =frac65.
2. Преобразуем sin x+cos x по формуле приведения и формуле суммы косинусов: sin x=cos left(fracpi 2-xright), cos x+sin x= cos x+cos left(fracpi 2-xright)= 2cos fracpi 4cos left(x-fracpi 4right)= sqrt 2cos left( x-fracpi 4right) = frac65.
Отсюда cos left(x-fracpi 4right) =frac<3sqrt 2>5. Значит, x-fracpi 4= arccos frac<3sqrt 2>5+2pi k, k in mathbb Z,
или x-fracpi 4= -arccos frac<3sqrt 2>5+2pi t, t in mathbb Z.
Поэтому x=fracpi 4+arccos frac<3sqrt 2>5+2pi k,k in mathbb Z,
или x =fracpi 4-arccos frac<3sqrt 2>5+2pi t,t in mathbb Z.
Найденные значения x принадлежат области определения.
б) Выясним сначала куда попадают корни уравнения при k=0 и t=0. Это будут соответственно числа a=fracpi 4+arccos frac<3sqrt 2>5 и b=fracpi 4-arccos frac<3sqrt 2>5.
1. Докажем вспомогательное неравенство:
Заметим также, что left( frac<3sqrt 2>5right) ^2=frac<18> <25>значит frac<3sqrt 2>5
2. Из неравенств (1) по свойству арккосинуса получаем:
Отсюда fracpi 4+0
Аналогично, -fracpi 4
0=fracpi 4-fracpi 4 fracpi 4
При k=-1 и t=-1 получаем корни уравнения a-2pi и b-2pi.
Bigg( a-2pi =-frac74pi +arccos frac<3sqrt 2>5,, b-2pi =-frac74pi -arccos frac<3sqrt 2>5Bigg). При этом -2pi
-2pi Значит, эти корни принадлежат заданному промежутку left( -2pi , -frac<3pi >2right).
При остальных значениях k и t корни уравнения не принадлежат заданному промежутку.
Действительно, если kgeqslant 1 и tgeqslant 1, то корни больше 2pi. Если kleqslant -2 и tleqslant -2, то корни меньше -frac<7pi >2.
Ответ
а) fracpi4pm arccosfrac<3sqrt2>5+2pi k, kinmathbb Z;
б) -frac<7pi>4pm arccosfrac<3sqrt2>5.
Задание №1175
Условие
а) Решите уравнение sin left( fracpi 2+xright) =sin (-2x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [0; pi ];
Решение
а) Преобразуем уравнение:
cos x+2 sin x cos x=0,
x =fracpi 2+pi n, n in mathbb Z;
x=(-1)^cdot fracpi 6+pi k, k in mathbb Z.
б) Корни, принадлежащие отрезку [0; pi ], найдём с помощью единичной окружности.
Указанному промежутку принадлежит единственное число fracpi 2.
Ответ
а) fracpi 2+pi n, n in mathbb Z; (-1)^cdot fracpi 6+pi k, k in mathbb Z;
б) fracpi 2.
Задание №1174
Условие
б) Найдите все корни этого уравнения, принадлежащие отрезку left[ -frac<3pi ><2>; -frac<pi >2 right].
Решение
а) Найдём ОДЗ уравнения: cos 2x neq -1, cos (pi +x) neq -1; Отсюда ОДЗ: x neq frac pi 2+pi k,
k in mathbb Z, x neq 2pi n, n in mathbb Z. Заметим, что при sin x=1, x=frac pi 2+2pi k, k in mathbb Z.
Полученное множество значений x не входит в ОДЗ.
Значит, sin x neq 1.
Разделим обе части уравнения на множитель (sin x-1), отличный от нуля. Получим уравнение frac 1<1+cos 2x>=frac 1<1+cos (pi +x)>, или уравнение 1+cos 2x=1+cos (pi +x). Применяя в левой части формулу понижения степени, а в правой — формулу приведения, получим уравнение 2 cos ^2 x=1-cos x. Это уравнение с помощью замены cos x=t, где -1 leqslant t leqslant 1 сводим к квадратному: 2t^2+t-1=0, корни которого t_1=-1 и t_2=frac12. Возвращаясь к переменной x , получим cos x = frac12 или cos x=-1, откуда x=frac pi 3+2pi m, m in mathbb Z, x=-frac pi 3+2pi n, n in mathbb Z, x=pi +2pi k, k in mathbb Z.
б) Решим неравенства
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 ,
2) -frac<3pi >2 leqslant -frac pi 3+2pi n leqslant -frac pi
3) -frac<3pi >2 leqslant pi+2pi k leqslant -frac pi 2 , m, n, k in mathbb Z.
1) -frac<3pi >2 leqslant frac<pi >3+2pi m leqslant -frac pi 2 , -frac32 leqslant frac13+2m leqslant -frac12 -frac<11>6 leqslant 2m leqslant -frac56 , -frac<11> <12>leqslant m leqslant -frac5<12>.
Нет целых чисел, принадлежащих промежутку left [-frac<11><12>;-frac5<12>right] .
2) -frac <3pi>2 leqslant -frac<pi >3+2pi n leqslant -frac<pi ><2>, -frac32 leqslant -frac13 +2n leqslant -frac12 , -frac76 leqslant 2n leqslant -frac1<6>, -frac7 <12>leqslant n leqslant -frac1<12>.
Нет целых чисел, принадлежащих промежутку left[ -frac7 <12>; -frac1 <12>right].
3) -frac<3pi >2 leqslant pi +2pi kleqslant -frac<pi >2, -frac32 leqslant 1+2kleqslant -frac12, -frac52 leqslant 2k leqslant -frac32, -frac54 leqslant k leqslant -frac34.
Этому неравенству удовлетворяет k=-1, тогда x=-pi.
Ответ
а) frac pi 3+2pi m; -frac pi 3+2pi n; pi +2pi k, m, n, k in mathbb Z;
Тригонометрические уравнения и преобразования
Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. К их числу прежде всего относятся простейшие тригонометрические уравнения, т.е. уравнения вида $sin x=a, cos x=a, tg x=a$, где $а$ – действительное число.
Перед решением уравнений разберем некоторые тригонометрические выражения и формулы.
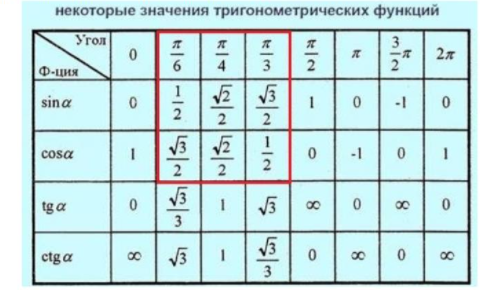
Значения тригонометрических функций некоторых углов
| $α$ | $ 0$ | $<π>/<6>$ | $<π>/<4>$ | $<π>/<3>$ | $<π>/<2>$ | $π$ |
| $sinα$ | $ 0$ | $ <1>/<2>$ | $ <√2>/<2>$ | $ <√3>/<2>$ | $ 1$ | $ 0$ |
| $cosα$ | $ 1$ | $ <√3>/<2>$ | $ <√2>/<2>$ | $ <1>/<2>$ | $ 0$ | $ -1$ |
| $tgα$ | $ 0$ | $ <√3>/<3>$ | $ 1$ | $ √3$ | $ -$ | $ 0$ |
| $ctgα$ | $ -$ | $ √3$ | $ 1$ | $ <√3>/<3>$ | $ 0$ | $ -$ |
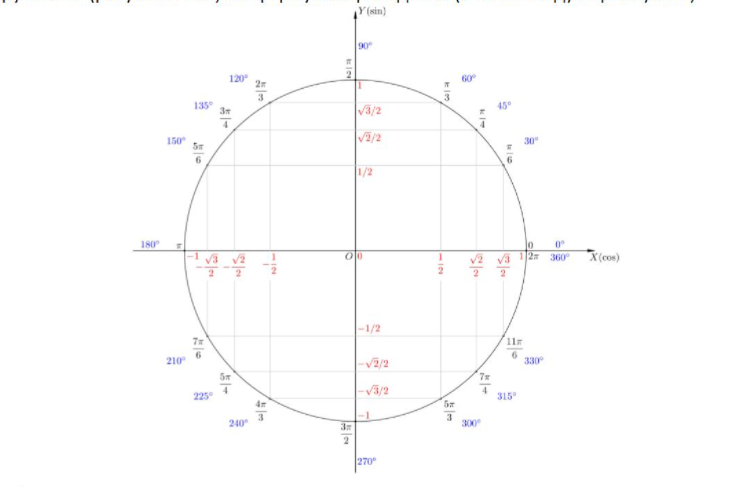
Периоды повтора значений тригонометрических функций
Период повторения у синуса и косинуса $2π$, у тангенса и котангенса $π$
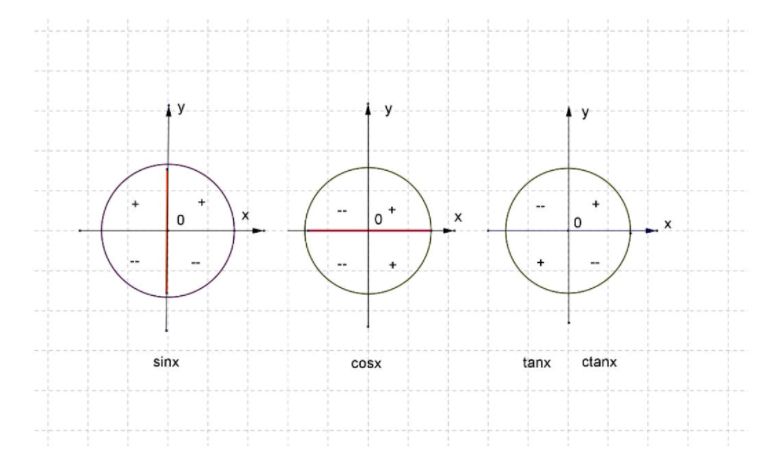
Знаки тригонометрических функций по четвертям
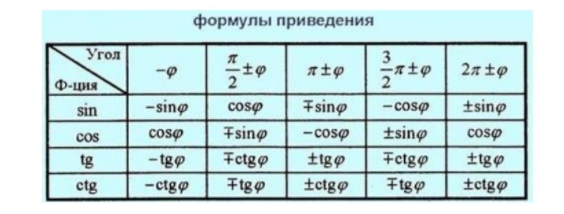
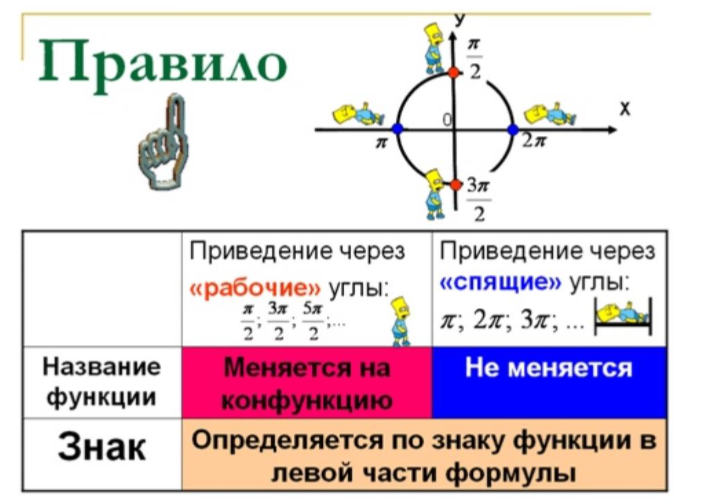
Эта информация нам пригодится для использования формул приведения. Формулы приведения необходимы для понижения углов до значения от $0$ до $90$ градусов.
Чтобы правильно раскрыть формулы приведения необходимо помнить, что:
- если в формуле содержатся углы $180°$ и $360°$ ($π$ и $2π$), то наименование функции не изменяется; (если же в формуле содержатся углы $90°$ и $270°$ ($<π>/<2>$ и $<3π>/<2>$), то наименование функции меняется на противоположную (синус на косинус, тангенс на котангенс и т. д.);
- чтобы определить знак в правой части формулы ($+$ или $-$), достаточно, считая угол $α$ острым, определить знак преобразуемого выражения.
Преобразовать $сos(90° + α)$. Прежде всего, мы замечаем, что в формуле содержится угол $90$, поэтому $cos$ измениться на $sin$.
Чтобы определить знак перед $sinα$, предположим, что угол $α$ острый, тогда угол $90° + α$ должен оканчиваться во 2-й четверти, а косинус угла, лежащего во 2-й четверти, отрицателен. Поэтому, перед $sinα$ нужен знак $-$.
$сos(90° + α)= — sinα$ — это конечный результат преобразования
Четность тригонометрических функций
Косинус четная функция: $cos(-t)=cos t$
Синус, тангенс и котангенс нечетные функции: $sin(-t)= — sin t; tg(-t)= — tg t; ctg(-t)= — ctg t$
Тригонометрические тождества
- $tgα=/$
- $ctgα=/$
- $sin^2α+cos^2α=1$ (Основное тригонометрическое тождество)
Из основного тригонометрического тождества можно выразить формулы для нахождения синуса и косинуса
Вычислить $sin t$, если $cos t = <5>/ <13>; t ∈(<3π>/<2>;2π)$
Найдем $sin t$ через основное тригонометрическое тождество. И определим знак, так как $t ∈(<3π>/<2>;2π)$ -это четвертая четверть, то синус в ней имеет знак минус
источники:
http://academyege.ru/theme/trigonometricheskie-uravneniya-3.html
http://examer.ru/ege_po_matematike/teoriya/trigonometricheskie_vyrageniya
Привет! На связи методический отдел федеральной сети курсов ЕГЭ и ОГЭ Lancman School («Ланцман скул»). Сегодня мы расскажем о том, как готовиться к ЕГЭ по профильной математике 2022 года.
Нелюбовь к тригонометрии в 10-11 классах может побить разве что страх перед стереометрией. Обычно опасение вызывают бесконечные столбцы формул и таблицы, которые заставляют учить для работы с тригонометрическими выражениями.
Но в ЕГЭ с тригонометрией всё достаточно просто. В первую очередь потому, что наизусть учить формул нужно даже меньше, чем для логарифмов. Вот популярный сборник формул для алгебры 10-11 класса. В нем мы выделили красным то, что нужно реально учить для экзамена.
Видно, что номинально объем по тригонометрии в 2 раза превосходит всю остальную алгебру (в этом сборнике нет разве что производной). А вот почему на деле так мало нужно учить наизусть – мы и расскажем ниже.
1. Справочные материалы
Во-первых, несколько формул дадут прямо на самом экзамене (речь про профильный ЕГЭ по математике), вместе с КИМами. Вот они:
2. Где и какая тригонометрия встречается на ЕГЭ
Формулы из третьего, самого правого столбца в большом сборнике формул либо уже есть среди этой пятерки выше, либо попросту не встречаются при решении ЕГЭшных задач. В крайнем случае что-то можно за несколько секунд вывести из этих пяти формул. Например,
Давайте тут же разберемся, где вообще можно встретить тригонометрию в профильной математике – чтоб вы понимали, стоит ли вся игра свеч.
А вообще-то стоит. Тригонометрия может попасться в целых 4 из 18 заданий ЕГЭ.
1) Задание 4. Преобразование выражений. Пример:
2) Задание 7. Практическая работа с формулами. Пример:
3) Задание 12. Уравнения, письменная часть. Пример:
4) Задание 17. Выражение с параметром, письменная часть. Пример:
В Задании 17, пожалуй, совсем редко встречается тригонометрия, но в остальных точно нужно быть к ней готовым. При этом самое большое разнообразие задач бывает в Задании 4.
Получается, нужно сфокусироваться на среднем столбце из большого сборника формул. И тут начинается самое интересное.
3. Большинство формул выводится
В самом деле, посмотрите на обведенные формулы в среднем столбце. Их очень мало, верно? Давайте разбираться по порядку с этим сборником, пойдем по его разделам.
1) Основные тождества
Из этих тождеств в ЕГЭ используется определение тангенса и котангенса (слева), это и правда надо выучить. А все остальное – либо следует или выводится из этих определений (попробуйте, например, перемножить дроби у тангенса и котангенса), либо уже дано в справочных материалах.
2) Тригонометрические уравнения
Вместо заучивания кучи этих формул лучше заняться изучением тригонометрической окружности. Все равно для более уверенного решения №12 – особенно пункта б) – потребуется в ней хорошо ориентироваться. Возможно, на изучение окружности потребуется примерно столько же времени, что и на заучивание соответственных формул. Но, во-первых, в отличие от механически выученного материала – практический навык не пропадет из памяти из-за волнения и стресса на экзамене. Во-вторых, именно работа с окружностью поможет сориентироваться в более сложных и непривычных ситуациях.
3) Значения тригонометрических функций от разных углов
В таблице предлагается выучить в сумме значений больше в 5 раз, чем предлагаем мы (обведено красным). И это еще не самая обширная таблица.
4) Формулы приведения
Как раз в виде формул заучивать эту тему – крайне неблагодарное дело. Приглядитесь: с учетом различных знаков из таблицы ниже придется извлечь и выучить 36 формул, едва отличающихся друг от друга!
Первый столбец вообще объясняется четностью-нечетностью функций и легко показывается (и вспоминается) через окружность. Другие формулы лучше не заучивать, а запомнить простой алгоритм в 2 шага. Сейчас мы им поделимся.
Шаг 2. Если исходная функция при исходном угле положительна, то знак перед выражением после «отбрасывания» не меняется. Если отрицательная – меняется на противоположный (или, можно сказать, происходит домножение на –1). В какой четверти какая функция положительна/отрицательна лучше не заучивать (см. рисунок ниже), а ориентироваться на оси.
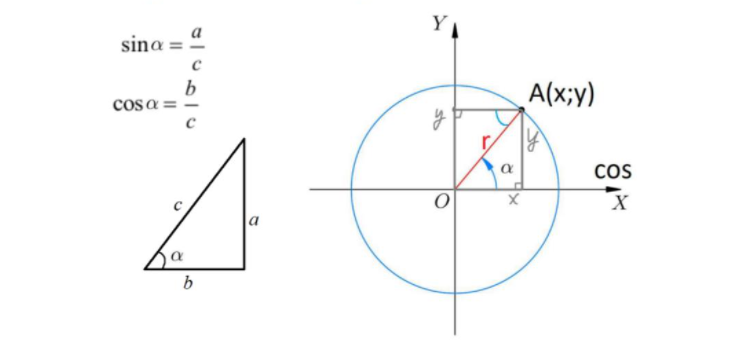
Да, почему ось Y – ось sin, а ось X – ось cos весьма легко понять, не заучивая этот факт. Вспомните определение, например, косинуса из геометрии: «прилежащий катет делить на гипотенузу». А теперь подставьте вместо прилежащего катета координату по оси X для треугольника, скажем, в 30° и вспомните, что в тригонометрической окружности r=1.
Вот и разобрались со всеми формулами. Ведь третий столбец в большом списке учить вообще не надо, как мы писали выше.
Конечно, ответ в этой статье получился сложнее, чем просто «учите вот этот и этот параграф наизусть», потому что изучать всегда сложнее, чем заучивать. Да еще и самостоятельно. Поэтому желаем вам найти преподавателя, который прислушается к вашим запросам и учтет индивидуальные особенности вашего стиля обучения. И – если у вас возникнут проблемы с запоминанием – сможет показать, как разобраться с любой сложной темой, не заучивая механически большие объемы материала наизусть.
Хочешь БЕСПЛАТНО разобрать с опытным преподавателем все детали новых усложнённых вариантов ЕГЭ по профильной математике 2022 года — приходи на пробное занятие в Lancman School. Мы 13 лет готовим к ЕГЭ на высокие баллы и знаем об экзаменах и поступлении в хорошие вузы буквально всё. Решишь продолжить готовиться к ЕГЭ вместе с нами весь год — дадим скидку после бесплатного пробного занятия. Любой вопрос смело пиши сюда.
Если ты живешь не в Москве, но хочешь заниматься с лучшими столичными репетиторами и сдать ЕГЭ на 80+ баллов, то регистрируйся на наши онлайн-курсы. В этом году мы включили в договор пункт, гарантирующий поступление на бюджет в любой вуз страны. Если ученик будет соблюдать все обговоренные условия, он обязательно поступит. В противном случае мы вернём деньги. Первое пробное занятие БЕСПЛАТНО.
Обложка поста: pixabay.com
Скачать материал

Скачать материал


- Сейчас обучается 23 человека из 17 регионов


- Сейчас обучается 99 человек из 37 регионов


- Курс добавлен 16.12.2022
- Сейчас обучается 20 человек из 14 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Задание №9 в КИМах ЕГЭ по математике профильного уровня
(2022 год)Решение задач по теме
«Графики тригонометрических функций»
Презентация подготовлена
учителем математики
МАОУ «Гимназия №1 Октябрьского района г. Саратова»
Гришиной Ириной Владимировной -
2 слайд
Задача №1 (по материалам сайта prof.mathege.ru).
На рисунке изображён график функции
y = a ∙sin 𝑥 + b.
Найдите a и b. -
3 слайд
Решение.
Рассматривая внимательно данный рисунок, определим «цену деления» на каждой из координатных осей.
На оси Ох одно деление
имеет длину 𝜋 4 ;
на оси Оу одно деление
имеет длину 0,5. -
4 слайд
Решение (стр.2)
Обратим внимание на то, что составители задач выделили на заданном графике две точки с легко читаемыми координатами.
Назовём эти точки А и В.
Определяем координаты точек: А(0;1,5), В( 𝜋 2 ; 3,5). -
5 слайд
Решение (стр. 3)
Так как точки А(0;1,5) и В( 𝜋 2 ; 3,5) принадлежат графику функции
y = a ∙sin 𝑥 + b, то подстановка их координат в эту формулу должна приводить к верным числовым равенствам.
Подставим координаты
А и В в формулу
у = a ∙sin 𝑥 + b. -
6 слайд
Решение (стр. 4)
Подставляем координаты точки А(0;1,5) :
1,5 = а 𝑠𝑖𝑛 0+𝑏 ;так как 𝑠𝑖𝑛 0=0, то
имеем 1,5 = а∙0+ b,
то есть b = 1,5.Таким образом, формула функции приобретает вид
y = a ∙sin 𝑥 + 1,5.Остаётся найти a.
-
7 слайд
Решение (стр. 5)
Теперь в уточнённую формулу функции, то есть
y = a sin 𝑥 + 1,5, подставим координаты второй точки – точки В( 𝜋 2 ; 3,5): 3,5 = a sin 𝜋 2 + 1,5;
учтём, что sin 𝜋 2 = 1, имеем равенство
3,5 = a ∙ 1 + 1,5;
получаем, что а = 2.
Ответ. а = 2, b = 1,5. Функция, график которой представлен на данном рисунке, имеет вид
y = 2 sin 𝑥 + 1,5. -
8 слайд
Задача №2 (по материалам сайта prof.mathege.ru).
На рисунке изображён график функции
y = a c𝑜𝑠 𝑥 + b.
Найдите a и b. -
9 слайд
Решение.
Как и в предыдущей задаче, рассматривая данный рисунок, определим «цену деления» на каждой из координатных осей.
На оси Ох одно деление
имеет длину 𝜋 4 ;
на оси Оу одно деление
имеет длину 0,5. -
10 слайд
Решение (стр.2)
Видим на заданном графике две точки с читаемыми легко координатами.
Назовём эти точки А и В.
Определяем координаты точек: А( ̶ 𝜋 2 ; ̶ 1),
В(0;0,5). -
11 слайд
Решение (стр. 3)
Так как точки А( ̶ 𝜋 2 ; ̶ 1) и В(0;0,5) принадлежат графику функции
y = a cos 𝑥 + b, то при подстановке их координат в эту формулу должны получаться верные числовые равенства.
Подставим координаты
А и В в формулу
y = a cos 𝑥 + b. -
12 слайд
Решение (стр. 4)
Подставляем координаты точки А( ̶ 𝜋 2 ; ̶ 1) :
̶ 1 = а 𝑐𝑜𝑠( ̶ 𝜋 2 ) +𝑏 ;так как 𝑐𝑜𝑠( ̶ 𝜋 2 ) =0, то
имеем ̶ 1 = а∙0+ b,
то есть b = ̶ 1 .Таким образом, формула функции приобретает вид
y = a 𝑐𝑜𝑠 𝑥 ̶ 1 .Остаётся найти a.
-
13 слайд
Решение (стр. 5)
Теперь в уточнённую формулу функции, то есть
y = a cos 𝑥 ̶ 1, подставим координаты второй точки – точки В(0;0,5):
0,5 = a ∙𝑐𝑜𝑠 0 ̶ 1;
так как 𝑐𝑜𝑠 0 = 1, то имеем равенство
0,5 = a ∙ 1 ̶ 1;
откуда получаем, что а = 1,5.Ответ. а = 1,5, b = ̶ 1. Функция, график которой представлен на данном рисунке, имеет вид
y = 1,5 cos 𝑥 ̶ 1. -
14 слайд
Задача №3 (по материалам сайта prof.mathege.ru).
На рисунке изображён график функции
y = a 𝑡𝑔 𝑥 + b.
Найдите a и b. -
15 слайд
Решение.
Определяем
«цену деления» на каждой из координатных осей.
На оси Ох одно деление
имеет длину 𝜋 4 ;
на оси Оу одно деление
имеет длину 0,5. -
16 слайд
Решение (стр.2)
Видим на заданном графике выделенные составителями задачи две точки.
Назовём эти точки А и В.
Определяем координаты точек: А(0; ̶ 1,5),
В( 𝜋 4 ;0,5). -
17 слайд
Решение (стр. 3)
Так как точки А(0; ̶ 1,5) и В( 𝜋 4 ;0,5) принадлежат графику функции
y = a 𝑡𝑔 𝑥 + b, то при подстановке их координат в эту формулу должны получаться верные числовые равенства.
Подставим координаты
А и В в формулу
y = a 𝑡𝑔 𝑥 + b. -
18 слайд
Решение (стр. 4)
Подставляем координаты точки А(0; ̶ 1,5) ) :
̶ 1,5 = а 𝑡𝑔0 +𝒃 ;так как 𝑡𝑔0 =0, то
имеем ̶ 1,5 = а∙0+ b,
то есть b = ̶ 1,5 .Таким образом, формула функции приобретает вид
y = a 𝒕𝒈 𝒙 ̶ 1,5 .Остаётся найти a.
-
19 слайд
Решение (стр. 5)
Теперь в уточнённую формулу функции, то есть
y = a 𝒕𝒈 𝒙 ̶ 1,5, подставим координаты второй точки –
точки В( 𝜋 4 ;0,5) :
0,5 = a ∙𝑡𝑔 𝜋 4 ̶ 1,5;
так как 𝑡𝑔 𝜋 4 = 1, то имеем равенство
0,5 = a ∙ 1 ̶ 1,5;
откуда получаем, что а = 2.Ответ. а = 2, b = ̶ 1,5. Функция, график которой представлен на данном рисунке, имеет вид
y = 2 tg 𝑥 ̶ 1,5.
Краткое описание документа:
Презентация на тему «Тригонометрические функции в заданиях №9 ЕГЭ 2022 года» даёт подробные решения прототипов заданий, связанных с графиками тригонометрических функций, что позволит учащимся 10-11 классов самостоятельно обучиться решению таких задач. Учитель математики может использовать данную презентацию при проведении уроков подготовки к ЕГЭ.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 156 856 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Материал подходит для УМК
-
«Алгебра и начала математического анализа», Колягин Ю.М., Ткачёва М.В. и др.
Тема
§ 4. Свойства функции y = sinx и ее график
Больше материалов по этой теме
Другие материалы


- 12.08.2022
- 41
- 0

- 12.08.2022
- 38
- 1

- 12.08.2022
- 107
- 7
- 12.08.2022
- 99
- 0
- 12.08.2022
- 92
- 0
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
ЕГЭ по математике — Профиль 2022. Открытый банк заданий с ответами.
- Главная
- Учебники
- Алгебра, 11 класс
- ЕГЭ 2022, задание №12, уравнения тригонометрии с ограничениями
ЕГЭ 2022, задание №12, уравнения тригонометрии с ограничениями
Алгоритм: Решение уравнений с ограничениями: .
-
Надо выписать ОДЗ — условия: условия существования выражений в уравнении. Решить получившиеся неравенства.
-
На тригонометрической окружности Е.Т.О. отметить области, промежутки точек, выполняющих условия ОДЗ.
-
Решить уравнение, отметить точки на Е.Т.О. , соответствующие полученным сериям решений.
-
Выбрать те точки, которые «попали» в допустимые промежутки, области. Какие числа-углы соответствуют этим точкам?
-
Написать серии для этих точек — эти серии и будут корнями нашего уравнения.
-
Выписать несколько конкретных корней. Перебрать разные $n$, $m$ целые числа, игнорируя заведомо не попадающие в ограничения.
-
Проверить каждый кандидат — корень: удовлетворяет ли условиям ограничения, входит ли в требуемый промежуток?
Задача 1: а) Решите уравнение $left(sin^2frac{x}{2}+frac{3cdot cos x}{2}right)left(sqrt{3}ctg x+1right)sqrt{-7sin x}=0$ б) Укажите корни этого уравнения, принадлежащие отрезку $left[-4pi;-frac{pi}{2}right]$ .
- ОДЗ: под радикалом $-7sin xge0$ ; Условие на существование котангенса $xnepi n$ — тоже самое, что $sin xne0$;
- Итоговое ОДЗ: $sin x<0$ — корнями могуть быть углы из 3-ей и 4-ой четверти, в нижней части Е.Т.О окружности.
- Решаем уравнение: здесь произведение нескольких множителей равно 0. Значит, распад на случаи — каждый множитель = 0.
- Факт: «Произведение сравнить с нулем можно свести к сравнению с нулем каждого множителя»:
- Уравнение: $Acdot Bcdot C=0$ $Rightarrow$ I случай $A=0$ , II случай $B=0$ , III случай $C=0$
- Последнее $sqrt{-7sin x}=0$ незачем решать т.к. мы уже установили при ОДЗ, что $sin xne0$ из-за присутствия котангенса.
- I случай: $sin^2frac{x}{2}+frac{3cdot cos x}{2}=0$ .
- Какие здесь углы? $frac{x}{2}$ и $x$ . Значит, можем свести к одному углу!
- По формуле удвоенного угла $cos x=1-2sin^2frac{x}{2}$ сможем прийти к замене $y=sinfrac{x}{2}$. Но, решим по-другому …
- по формуле понижения степени — половинного угла: $frac{1-cos x}{2}+frac{3cdot cos x}{2}=0$ придем к простому
- $1+2cos x=0$ $Rightarrow$ $cos x=-frac{1}{2}$ его корни: $x=frac{2pi}{3}+2pi n$ $x=-frac{2pi}{3}+2pi m$
- Смотрим на Е.Т.О. — из этих двух точек-серий по ОДЗ нас устраивает только из 3-ей четверти: $x=-frac{2pi}{3}+2pi m$
- II случай: $sqrt{3}ctg x+1=0$ «если в уравнении лишь одна функция, ее следует выразить …»:
- $ctg x=-frac{sqrt{3}}{3}$ корни: 2 точки-серии $x=-frac{pi}{3}+pi k$. Устраивает по ОДЗ: $x=-frac{pi}{3}+2pi k$
- ответ a): $x=-frac{2pi}{3}+2pi m$ $x=-frac{pi}{3}+2pi k$ . (Две точки из нижней части Е.Т.О.).
- Пункт б): Ищем корни из требуемого промежутка $left[-4pi;-frac{pi}{2}right]$. Выпишем несколько возможных кандидатов для каждой серии:
- Из I серии: $-frac{2pi}{3}+2pi$, $-frac{2pi}{3}$, $-frac{2pi}{3}-2pi=-frac{8pi}{3}$, $-frac{2pi}{3}-4pi$. Входит: 2-ой и 3-ий.
- Из II серии: $-frac{pi}{3}+2pi$, $-frac{pi}{3}$, $-frac{pi}{3}-2pi=-frac{7pi}{3}$, $-frac{pi}{3}-4pi$. Попал лишь 3-ий.
- Требуемому ограничению удовлетворяют корни, ответ б): $-frac{2pi}{3}$, $-frac{7pi}{3}$, $-frac{8pi}{3}$,
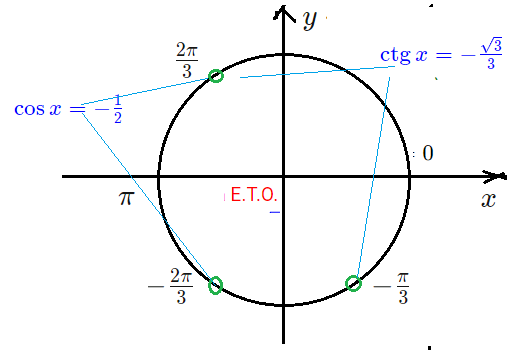
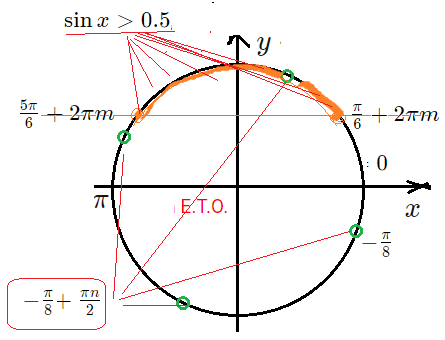
Задача 2: а) Решите уравнение $frac{3cos^2 4x-7left(sin 4x+1right)}{sqrt{2sin x-1}}=0$ б) Укажите корни этого уравнения, принадлежащие отрезку $left[-4pi;frac{2pi}{3}right]$ .
- ОДЗ — условия: знаменатель не ноль, под радикалом неотрицательно: $2sin x-1>0$
- Надо понять какие точки удовлетворяют ОДЗ на тригонометрической окружности Е.Т.О. Реши неравенство.
- Но пока уравнение: $2sin x-1=0$ $sin x=0.5$ $x=frac{pi}{6}+2pi m$ $x=frac{5pi}{6}+2pi m$
- Отметим эти точки-серии на Е.Т.О. Решение неравенства — это точки, в которых $sin x>0.5$ , значит точки с $y$ — координатой выше $>0.5$ .
- Значит, неравенство и ОДЗ выполняется в точках дуги , верхней части окружности между точками $frac{pi}{6}$ и $frac{5pi}{6}$.
- Теперь решаем само уравнение: «Дробь = 0 $Rightarrow$ числитель дроби = 0″. Алгоритм: $frac{A}{B}=0$ $Rightarrow$ $A=0$
- Итак: $3cos^24x-7left(sin4x+1right)=0$ У нас 2 функции, 1 аргумент. Выразим первую через вторую:
- $3cos^24x=1-sin^24x$ — Основное тождество, $3left(1-sin^24xright)-7left(sin4x+1right)=0$ .
- Упростим: $3sin^24x+7sin4x+4=0$ 1 функция, 1 аргумент — все готово к методу замены:
- замена $y=sin4x$ подстановка: $3y^2+7y+4=0$ корни: $y=-1$ $y=-frac{4}{3}$
- $y=-1$ возвратное: $sin4x=-1$ $Rightarrow$ $4x=-frac{pi}{2}+2pi n$ $Rightarrow$ $x=-frac{pi}{8}+frac{pi n}{2}$
- $y=-frac{4}{3}$ возвратное: $sin4x=-frac{4}{3}$ — нет решениий, т.к $-frac{4}{3}<-1$ , а синус не может стать меньше $<-1$
- Отметим серию $x=-frac{pi}{8}+frac{pi n}{2}$ — это точки, получающиеся от точки $-frac{pi}{8}$ прокруткой четверть оборотов $frac{pi}{2}$.
- Получаются четыре точки на Е.Т.О.: $-frac{pi}{8}$, $frac{3pi}{8}$, $7frac{pi}{8}$, $-5frac{pi}{8}$.
- Из этих 4-х точек в интервале ОДЗ $left(frac{pi}{6};frac{5pi}{6}right)$ находится только точка $frac{3pi}{8}$ .
- ОДЗ удволетворяют углы: $frac{3pi}{8}$ и его $2pi$ — прокуртки. ответ а): $frac{3pi}{8}+2pi n$
- Пункт б): Ищем корни из требуемого промежутка . Выпишем несколько возможных кандидатов из серии $frac{3pi}{8}+2pi n$:
- кандидаты: $frac{19pi}{8}$ $frac{3pi}{8}$ $-frac{13pi}{8}$ $-frac{29pi}{8}$ $-frac{45pi}{8}$ . Какие из них попадают в интервал $left[-4pi;frac{2pi}{3}right]$
- Проверка принадлежности промежутку ограничения: ответ б): $frac{3pi}{8}$ $-frac{13pi}{8}$ $-frac{29pi}{8}$,
Послесловие: Какие навыки, умения, смыслы, понятия надо знать?
- Е.Т.О — связь углов, точек на окружности, серии углов, прокрутки в пол-оборота, полный оборот, части.
- Формулы решения простейших тригонометрических уравнений, интерпретация в виде точек на Е.Т.О.
- Решение неравенств, изображение решений на Е.Т.О. Перевод точек на серии углов и наоборот.
- Анализ ОДЗ: радикалы, знаменатели, тангенс-котангенс. Анализ условий ограничений. Интерпретация на Е.Т.О.
- Методы решения тригонометрических уравнений: простейших, метод замены, разложение на множители, понижение степени, однородные.











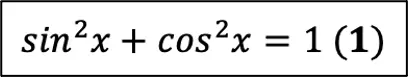
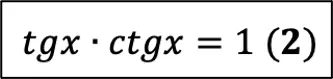
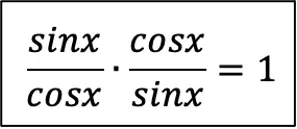
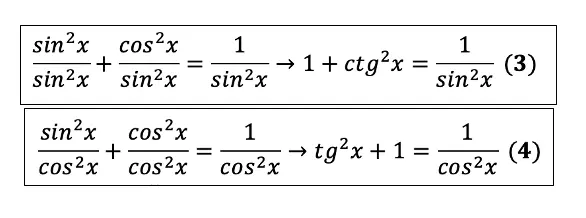
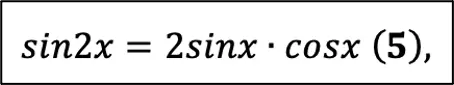
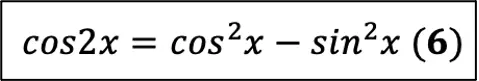
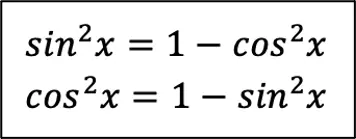
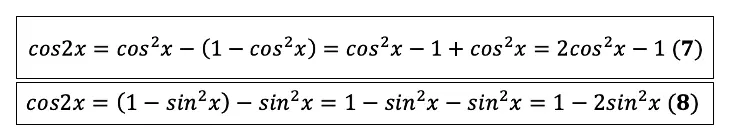
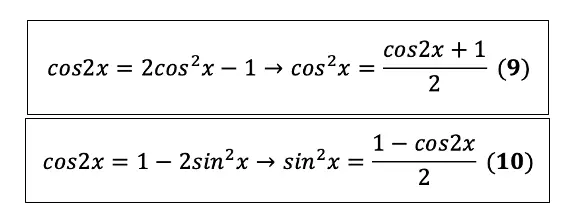
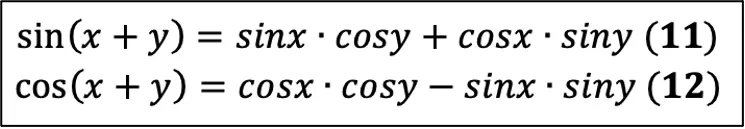
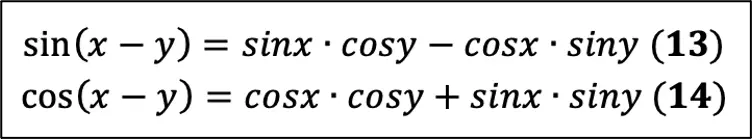



.png)