Критерии
Оценивание
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
| № задания | 1-11 | 12, 14, 15 | 13, 16 | 17, 18 | Всего |
|---|---|---|---|---|---|
| Баллы | 1 | 2 | 3 | 4 | 31 |
Экзаменационная работа состоит из двух частей, включающих в себя 18 заданий. Часть 1 содержит 11 заданий базового уровня сложности с кратким ответом. Часть 2 содержит 7 заданий с развёрнутым ответом повышенного и высокого уровней сложности.
На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).
Ответы к заданиям 1–11 записываются в виде целого числа или конечной десятичной дроби. Числа запишите в поля ответов в тексте работы, а затем перенесите в бланк ответов № 1, выданный на экзамене!
При выполнении работы Вы можете воспользоваться справочными материалами, выдаваемыми вместе с работой.
Разрешается использовать только линейку, но можно сделать циркуль своими руками. Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.
На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.
Шкалирование
| Первичный | Тестовый | Оценка |
|---|---|---|
| 5-6 | 27-34 | 3 |
| 7-8 | 40-46 | 4 |
| 9-10 | 52-58 | |
| 11-12-13 | 64-66-68 | 5 |
| 14-15-16 | 70-72-74 | |
| 17-18-19 | 76-78-80 | |
| 20-21-22 | 82-84-86 | |
| 23-24-25 | 88-90-92 | |
| 26-27-28 | 94-96-98 | |
| 29-30-31 | 100 |
| Первичный балл / Тестовый балл |
5/27 | 6/34 | 7/40 | 8/46 | 9/52 | 10/58 | 11/64 | 12/66 | 13/68 | 14/70 |
|---|---|---|---|---|---|---|---|---|---|---|
| 15/72 | 16/74 | 17/76 | 18/78 | 19/80 | 20/82 | X / 2X+42 | 29+ / 100 |
Задание 1
Найдите величину тупого угла между биссектрисами острых углов прямоугольного треугольника. Ответ дайте в градусах.
Ответ: 135
Скрыть
Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть
Так как дан прямоугольный треугольник, то сумма острых углов составляет 90 градусов $$(angle A+angle B=90).$$
Биссетрисы делят углы пополам, следовательно, сумма половин острых углов составит 45 градусов $$(0,5angle A+0,5angle B=45).$$
Тогда величина тупого угла между биссектрисами будет $$180-45=135^{circ}$$
Задание 2
В кубе $$ABCDA_1B_1C_1D_1$$ все ребра равны $$sqrt{6}.$$ Найдите расстояние от точки $$С_1$$ до прямой $$ВА_1.$$
Ответ: 3
Скрыть
$$rho(C_1;BA_1)=h,$$ где $$h$$ — высота $$Delta C_1BA_1,$$ опущенная из $$C_1.$$
Из $$Delta A_1C_1D_1:$$
$$C_1A_1=sqrt{(sqrt{6})^2+(sqrt{6})^2}=sqrt{12}$$
$$Delta C_1BA_1$$ — равносторонний, тогда $$h=C_1cdotsin C_1BA_1=sqrt{12}cdotfrac{sqrt{3}}{2}=3$$
Задание 3
В плацкартном вагоне 54 места. Четные места — верхние, нечетные — нижние. Места с 37 по 54 — боковые. Пассажир Р. покупает билет. При покупке билета место определяется случайно. Найдите вероятность того, что пассажиру Р. достанется нижнее не боковое место. Ответ округлите до сотых.
Ответ: 0,33
Скрыть
Нижние небоковые места имеют нечетные номера в диапазоне от 1 до 36. Таких чисел 18.
$$P(A)=frac{18}{54}=frac{1}{3}approx0,33$$
Задание 4
Литье в болванках поступает из двух заготовительных цехов: из первого цеха — 70%, из второго цеха — 30%. Литье из первого цеха имеет 10% брака, литье из второго цеха — 20% брака. Случайно взятая болванка оказалась без дефекта. Найдите вероятность того, что она изготовлена первым цехом. Ответ округлите до сотых.
Ответ: 0,72
Скрыть
1. Рассматриваем следующие события и гипотезы:
•событие $$А$$ = {болванка без дефекта};
•гипотеза $$Н_1$$ = {болванка изготовлена первым цехом}, $$Р(Н_1)=70%=0,7$$
•гипотеза $$Н_2$$ = {болванка изготовлена вторым цехом}, $$Р(Н_2)=30%=0,3$$
2. Так как литье первого цеха имеет 10% брака, то 90% болванок, изготовленных первым цехом, не имеют дефекта, т.е. $$РН_1(А)=0,9.$$
Литье второго цеха имеет 20% брака, то 80% болванок, изготовленных вторым цехом, не имеют дефекта, т.е. $$РН_2(А)=0,8.$$
3. По формулу Бейеса найдем $$РА(Н_1)=0,7cdotfrac{0,9}{(0,7cdot0,9+0,3cdot0,8)}=frac{0,63}{0,87}approx0,72$$
Задание 5
Решите уравнение $$frac{sqrt{x^2-25}-12}{sqrt{-3x}}=0.$$
Ответ: -13
Скрыть
$$frac{sqrt{x^2-25}-12}{sqrt{-3x}}=0Leftrightarrowleft{begin{matrix} x^2-25=144\ -3x>0 end{matrix}right.Leftrightarrowleft{begin{matrix} x=pm13\ x<0 end{matrix}right.Leftrightarrow x=-13$$
Задание 6
Найдите $$log_asqrt[5]{a^4b^3},$$ если $$log_ba=-frac{1}{3}.$$
Ответ: -1
Скрыть
$$log_asqrt[5]{a^4b^3}=frac{1}{5}log_a a^4b^3=frac{1}{5}(log_a a^4+log_a b^3)=frac{1}{5}(4+3log_a b)=frac{1}{5}(4+frac{3}{log_b a})=$$
$$=frac{1}{5}(4+3:(-frac{1}{3}))=frac{1}{5}cdot(-5)=-1$$
Задание 7
На рисунке изображен график $$y=f'(x)$$ — производной функции $$f(x),$$ определенной на интервале $$(-8;3).$$ В какой точке отрезка $$[-5; 0]$$ функция $$f(x)$$ принимает наибольшее значение?
Ответ: -3
Скрыть
Известно, что производная положительная в окрестностях точек, где функция возрастает и отрицательная, где функция убывает. Анализ графика производной показывает, что на участке $$[-5;-3]$$ функция $$f(x)$$ возрастала, а затем, на участке $$[-3; 0]$$ – убывала. Следовательно, максимальное значение она приобретает в точке $$-3.$$
Задание 8
Два тела массой $$m = 2$$ кг каждое движутся с одинаковой скоростью $$v = 10$$ м/с под углом $$2alpha$$ друг к другу. Энергия (в джоулях), выделяющаяся при их абсолютно неупругом соударении, определяется выражением $$Q=mv^2sin^2alpha.$$ Под каким наименьшим углом $$2alpha$$ (в градусах) должны двигаться тела, чтобы в результате соударения выделилось не менее 50 джоулей?
Ответ: 60
Скрыть
Выразим квадрат синуса из формулы энергии:
$$sin^alpha=frac{Q}{mv^2}$$
Подставим сюда числовые величины, получим:
$$sin^2alpha=frac{50}{2cdot10^2}=frac{1}{4}$$
откуда
$$sinalpha=pmfrac{1}{2}$$
В задаче спрашивают наименьший угол и в физике углы берутся из положительной области, поэтому имеем уравнение
$$sinalpha=frac{1}{2}Rightarrow alpha=arcsinfrac{1}{2}=30^{circ}$$
И, окончательно, угол $$2alpha=2cdot30^{circ}=60^{circ}.$$
Задание 9
Байдарка в 10:00 вышла из пункта А в пункт В, расположенный в 15 км от А. Пробыв в пункте В 1 час 20 минут, байдарка отправилась назад и вернулась в пункт А в 18:00 того же дня. Определите (в км/ч) собственную скорость байдарки, если известно, что скорость течения реки 3 км/ч.
Ответ: 6
Скрыть
Пусть $$x$$ км в час – собственная скорость байдарки, тогда
$$(x+3)$$ км в час – скорость байдарки по течению,
$$(x–3)$$ км в час – скорость байдарки против течения.
$$frac{15}{x+3}$$ час. – время в пути по течению
$$frac{15}{x–3}$$ час. – время в пути против течения.
Всего байдарка была в движении ( по течению и против течения)
18:00 — 10:00 — 1 час 20 мин (стоянки) = 6 часов 40 мин = $$6frac{2}{3}$$ = $$frac{20}{3}$$
$$frac{15}{x+3}+frac{15}{x–3}=frac{20}{3}$$
Делим на 5:
$$frac{3}{x+3}+frac{3}{x–3}=frac{4}{3}$$
$$9x–27+9x+27=4(x^2–9)$$
$$4x^2–18x–36=0$$
$$2x^2–9x–18=0$$
$$D=(-9)^2-4cdot2cdot(-18)=81+144=225$$
$$x_1=frac{9+15}{4}=6$$
Второй корень отрицательный и не удовлетворяет смыслу задачи.
Задание 10
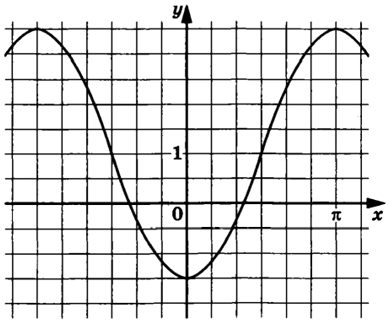
На рисунке изображен график функции $$f(x)=acdotcos x+b.$$ Найдите $$a.$$
Ответ: -2,5
Скрыть
График проходит через $$(0;-1,5)$$ и $$(frac{pi}{2};1).$$ Тогда:
$$left{begin{matrix} -1,5=acdotcos0+b\ 1=acdotcosfrac{pi}{2}+b end{matrix}right.Leftrightarrowleft{begin{matrix} -1,5=a+b\ b=1 end{matrix}right.Leftrightarrowleft{begin{matrix} a=-2,5\ b=1 end{matrix}right.$$
Задание 11
Найдите точку максимума функции: $$y=ln(x+9)-10x+7$$
Ответ: -8,9
Скрыть
$$y=ln(x+9)-10x+7$$
$$y’=frac{1}{x+9}-10$$
$$frac{1}{x+9}-10=0$$
$$frac{1}{x+9}=10$$
$$10x+90=1$$
$$10x=-89$$
$$x=-8,9$$
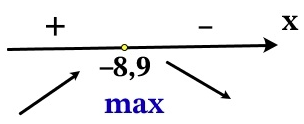
Определим знаки производной функции и изобразим поведение функции:
Точка максимума функции: $$x=-8,9.$$
Задание 12
А) Решите уравнение $$frac{6sin x-2cos2x-4cos^2x-3}{sqrt{7}sin x-3cos x}=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-4pi;-3pi]$$
Ответ: А)$$pi-arcsinfrac{3}{4}+2pi n,nin Z$$ Б)$$-3pi-arcsinfrac{3}{4}$$
Задание 13
В кубе ABCDA1B1C1D1 отмечены середины Р и Е отрезков АВ и AD соответственно.
А) Докажите, что прямые В1Е и СР перпендикулярны.
Б) Найдите расстояние между этими прямыми, если B1E=$$5sqrt{5}$$?
Ответ: $$frac{10}{3}$$
Задание 14
Решите неравенство: $$log_{2-5x}3+frac{1}{log_2(2-5x)}leqfrac{1}{log_6(6x^2-6x+1)}$$
Ответ: $$[-frac{1}{3};0).(frac{1}{5};frac{3-sqrt{3}}{6})$$
Задание 15
Первый банк предлагает открыть вклад с процентной ставкой 10%, а второй — 11%. Проценты по вкладу начисляются раз в год и прибавляются к текущей сумме вклада. Клиент сделал одинаковые вклады в оба банка. Через два года второй банк уменьшил процентную ставку по вкладу с 11% до Р%. Еще через год клиент закрыл оба вклада и забрал все накопившиеся средства, и оказалось, что второй банк принес ему больший доход, чем первый. Найдите наименьшее целое Р, при котором это возможно.
Ответ: 9
Задание 16
На стороне ВС треугольника АВС, в котором АВ < BC, взята точка D так, что BD = AB. Биссектриса BL пересекает отрезок AD в точке Р, отрезок СК — перпендикуляр к прямой AD.
А) Докажите, что $$frac{BC}{AB}-frac{DK}{AP}=1$$
Б) Найдите отношение площади треугольника АВР к площади четырехугольника CDPL, если AB : BC = 5 : 7.
Ответ: $$frac{30}{19}$$
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых уравнение:
$$2^{frac{2x}{1+x^2}}+acdotcos(frac{x^2-1}{x})+a^2=frac{5}{4}$$
имеет единственное решение.
Ответ: -1,5
Задание 18
На острове живут 3 серых, 28 бурых и 29 малиновых хамелеонов. При встрече двух хамелеонов разных цветов оба меняют свой цвет на третий (серый и бурый оба становятся малиновыми и т.п.).
А) Может ли в некоторый момент времени на острове оказаться 15 серых, 28 бурых и 17 малиновых хамелеонов?
Б) Может ли некоторый момент времени на острове оказаться 60 серых хамелеонов?
В) Какое наибольшее количество серых хамелеонов может оказаться на острове, при условии, что малиновых хамелеонов в этот момент времени ровно 2?
Ответ: А) да, Б) нет, В) 57
Новый тренировочный вариант №397 Алекса Ларина ЕГЭ 2023 по математике профильный уровень 11 класс с ответами и решением, который вышел на сайте 10 сентября 2022 года, по новой демоверсии ЕГЭ 2023 года ФИПИ.
Скачать вариант с ответами
Демоверсия ЕГЭ 2023 по математике
Тренировочный вариант 397 Ларина ЕГЭ 2023 по математике профиль
ларин-егэ2023-вариант-397-ответы
Ответы для варианта
1)Около окружности, радиус которой равен 8, описан многоугольник, площадь которого равна 208. Найдите периметр этого многоугольника.
Ответ: 52
2)В прямоугольном параллелепипеде АВСDА1B1C1D1 известны длины ребер: АВ = 11, AD = 20, AA1 = 4. Найдите расстояние от вершины С до центра грани АА1D1D.
Ответ: 15
3)Из слова «максимум» случайным образом выбирается одна буква. Найдите вероятность того, что будет выбрана буква, встречающаяся в этом слове только один раз.
Ответ: 0,625
4)Куб, все грани которого окрашены, распилен на 1000 кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что извлечённый наугад кубик будет иметь хотя бы одну окрашенную грань.
Ответ: 0,488
9)Имеется три одинаковых по массе сплава. Известно, что процентное содержание никеля во втором сплаве на 25 процентных пункта больше, чем в первом, а процентное содержание никеля в третьем сплаве на 4 процентных пункта больше, чем во втором. Из этих трёх сплавов получили четвертый сплав, содержащий 64% никеля. Сколько процентов никеля содержит первый сплав?
Ответ: 46
13)В правильной шестиугольной пирамиде SABCDEF сторона основания AB = 4, а боковое ребро SA = 7. Точка M лежит на ребре BC, причем BM = 1, точка K лежит на ребре SC, причем SK = 4. А) Докажите, что плоскость MKD перпендикулярна плоскости основания пирамиды. Б) Найдите объем пирамиды CDKM.
15)В июле 2026 года планируется взять кредит на три года. Условия его возврата таковы: — каждый январь долг будет возрастать на 20% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить одним платежом часть долга; — платежи в 2027 и в 2028 годах должны быть по 300 тыс. руб.; — к июлю 2029 года долг должен быть выплачен полностью. Известно, что платёж в 2029 году будет равен 417,6 тыс. руб. Какую сумму (в тыс. рублей) планируется взять в кредит?
Ответ: 700
16)Две окружности пересекаются в точках Р и Q. Через точку Р проведена прямая, пересекающая вторично первую из окружностей в точке А, а вторую – в точке В. Через точку Q также проведена прямая, пересекающая вторично первую окружность в точке С, а вторую – в точке D. А) Докажите, что прямые АС и BD параллельны. Б) Найдите наибольшее возможное значение суммы длин отрезков АВ и CD, если расстояние между центрами данных окружностей равно 1.
18)Издательство на выставку привезло несколько книг для продажи (каждую книгу привезли в единственном экземпляре). Цена каждой книги — натуральное число рублей. Если цена книги меньше 100 рублей, на неё приклеивают бирку «выгодно». Однако до открытия выставки цену каждой книги увеличили на 10 рублей, из‐за чего количество книг с бирками «выгодно» уменьшилось.
А) Могла ли уменьшиться средняя цена книг с биркой «выгодно» после открытия выставки по сравнению со средней ценой книг с биркой «выгодно» до открытия выставки?
Б) Могла ли уменьшиться средняя цена книг без бирки «выгодно» после открытия выставки по сравнению со средней ценой книг без бирки «выгодно» до открытия выставки?
В) Известно, что первоначально средняя цена всех книг составляла 110 рублей, средняя цена книг с биркой «выгодно» составляла 81 рубль, а средняя цена книг без бирки — 226 рублей. После увеличения цены средняя цена книг с биркой «выгодно» составила 90 рублей, а средняя цена книг без бирки — 210 рублей. При каком наименьшем количестве книг такое возможно?
Видео решение варианта Ларина
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
| 3655 | Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD=3RD. Прямые AR и PD пересекаются в точке Q , AD=2BC. a) Докажите, что точка Q – середина отрезка AR б) Найдите площадь треугольника APQ |
Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD=3RD ! Тренировочный вариант 221 от Ларина Задание 16 # Решение пункта Б | |
| 3471 | а) Решите уравнение cos(3x)/(2sin(x)+sqrt(2))=sin(x)/(2sin(x)+sqrt(2)) б) Найдите все корни уравнения, принадлежащие отрезку [0; pi]. |
а) Решите уравнение cos3x /(2sinx + sqrt2 = sinx /2sinx +sqrt2 ! Тренировочный вариант 399 от Ларина Задание 12 | |
| 3470 | В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней |
В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13 | |
| 3469 | Решите неравенство 64^x/(36^x-27^x)+(4(16^x-12^x))/(16^x-2*12^x+9^x). <= 16^(x+0.5)/(12^x-9^x). |
Решите неравенство 64^x / 36^x -27^x +4(16^x-12^x) /16^x -2*12^x+9^x <= 16^ x+0,5 / 12^x-9^x ! Тренировочный вариант 399 от Ларина Задание 14 |
|
| 3468 | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN |
На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16 | |
| 3467 | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ |
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16 | |
| 3466 | Найдите значение выражения ((root(4)(3)-root(4)(27))^2+7)((root(4)(3)+root(4)(27))^2-7) |
Найдите значение выражения ((root(4)(3) -root(4)(27))2 +7 ((root(4)(3)+root(4)(27))2 -7) ! Тренировочный вариант 398 от Ларина Задание 6 | |
| 3465 | Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве? |
Имеются два сплава, состоящие из цинка, меди и олова ! Тренировочный вариант 398 от Ларина Задание 9 | |
| 3464 | а) Решите уравнение sqrt(2sin(x)+sqrt(2))*log_{4}(2cos(x))=0 б) Найдите все корни уравнения, принадлежащие отрезку [-(5pi)/2; -pi]. |
а) Решите уравнение sqrt(2sinx +sqrt2) log4 2cosx = 0 ! Тренировочный вариант 398 от Ларина Задание 12 | |
| 3463 | SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN. а) Доказать, что плоскости SLK и MPN перпендикулярны б) Найдите длину отрезка PL, если длина ребра MN равна 4 |
SMNK – правильный тетраэдр ! Тренировочный вариант 398 от Ларина Задание 13 | |

Показана страница 1 из 89
- О сайте
- Карта сайта
- Пользовательское соглашение
- Политика конфиденциальности
© 2020-2023, ege314.ru, ОГЭ и ЕГЭ по математике | Генератор вариантов ЕГЭ 2023.
Частичное или полное копирование решений (включая графические элементы) с данного сайта для распространения на других ресурсах, в том числе и бумажных, строго запрещено. Все решения являются собственностью сайта.
Тренировочные варианты профильного ЕГЭ 2023 по математике с ответами.