Всего: 71 1–20 | 21–40 | 41–60 | 61–71
Добавить в вариант
15-го января планируется взять кредит в банке на некоторый срок (целое число месяцев). Условие его выплаты таковы:
− 1-го числа k-ого месяца долг возрастёт на 1% по сравнению с концом предыдущего месяца;
− со 2-го по 14-е число k-того месяца необходимо выплатить часть долга;
− 15-го числа k-того месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
На сколько месяцев планируется взять кредит, если известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит?
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 402 (C часть).
В июле планируется взять кредит в банке на сумму 20 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 30% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года.
На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн рублей?
Источник: А. Ларин: Тренировочный вариант № 238.
Банк планирует вложить на 1 год 40% имеющихся у него средств клиентов в проект Х, а остальные 60% в проект Y. Проект Х может принести прибыль в размере от 19% до 24% годовых, а проект Y — от 29% до 34% годовых. В конце года банк обязан вернуть деньги клиентам и выплатить им проценты по заранее установленной ставке. Определить наименьший и наибольший возможные уровни процентной ставки, при которых чистая прибыль банка составит не менее 10% и не более 15% годовых от суммарных вложений в проекты Х и Y.
Источник: А. Ларин. Тренировочный вариант № 366.
15‐го января планируется взять кредит в банке на 14 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15 число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 15% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант Ларина.
Семья Ивановых ежемесячно вносит плату за коммунальные услуги, телефон и электричество. Если бы коммунальные услуги подорожали на 50%, то общая сумма платежа увеличилась бы на 35%. Если бы электричество подорожало на 50%, то общая сумма платежа увеличилась бы на 10%. Какой процент от общей суммы платежа приходится на телефон?
Источник: А. Ларин: Тренировочный вариант № 106.
В июле планируется взять кредит в банке на сумму 28 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 9 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
В июле планируется взять кредит в банке на сумму 9 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 1,5 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
В июле планируется взять кредит в банке на сумму 17 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 10% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
Чему будет равна общая сумма выплат после полного погашения кредита, если наибольший годовой платёж составит 3,4 млн рублей?
Источник: Материалы для экспертов ЕГЭ 2016
Планируется выдать льготный кредит на целое число миллионов рублей на пять лет. В середине каждого года действия кредита долг заёмщика возрастает на 10% по сравнению с началом года. В конце 1-го, 2-го и 3-го годов заёмщик выплачивает только проценты по кредиту, оставляя долг неизменно равным первоначальному. В конце 4-го и 5-го годов заёмщик выплачивает одинаковые суммы, погашая весь долг полностью. Найдите наибольший размер кредита, при котором общая сумма выплат заёмщика будет меньше 8 млн.
В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс рублей. Условия его возврата таковы:
− каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017,2018 и 2019 долг остаётся равным S тыс. рублей;
− выплаты в 2020 и 2021 годах равны по 625 тыс. рублей;
− к июлю 2021 долг будет выплачен полностью.
Найдите общую сумму выплат за пять лет.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 509 (C часть).
Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27% больше, чем сумма, взятая им в кредит. Найдите r.
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С).
15-го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 20% больше суммы, взятой в кредит. Найдите r.
Источник: ЕГЭ — 2015. Основная волна по математике 04.06.2015. Вариант 2 (Часть С)., Задания 17 (С4) ЕГЭ 2015
15 января планируется взять кредит в банке на 6 месяцев в размере 1 млн руб. Условия его возврата таковы:
− Первого числа месяца долг увеличивается на r% по сравнению с концом предыдущего месяца, где r целое число.
− Со 2 по 14 число необходимо выплатить часть долга.
− 15 числа каждого месяца долг должен составлять некоторую сумму в соответствии с таблицей
| Месяц | Январь | Февраль | Март | Апрель | Май | Июнь | Июль |
| Долг | 1 | 0,6 | 0,4 | 0,3 | 0,2 | 0,1 | 0 |
Найдите наибольшее r, при котором сумма выплат будет меньше 1,25 млн руб.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 412. Запад (C часть).
В июле 2016 года планируется взять кредит в банке на пять лет в размере S тыс. рублей. Условия его возврата таковы:
− каждый январь долг возрастает на 20%;
− с февраля по июнь каждого года необходимо выплатить часть долга;
− в июле 2017-2019 долг остаётся S
− в 2020, 2021 выплаты по 360 тыс. руб.
− к июлю 2021 долг будет выплачен полностью
Найдите общую сумму выплат за 5 лет.
Источник: ЕГЭ по математике 06.06.2016. Основная волна.
В июле планируется взять кредит в банке на сумму 5 млн рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн рублей?
Источник: Задания 17 (С5) ЕГЭ 2017, ЕГЭ — 2017. Основная волна 02.06.2017. Вариант 419 (C часть)., Задания 17 ЕГЭ–2020
В июле 2018 года планируется взять кредит в банке на шесть лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 2% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите S, если общая сумма выплат после полного погашения кредита составила 327 тысяч рублей.
В июле 2018 года планируется взять кредит в банке на шесть лет в размере S тыс. рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на 1% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
— в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите S, если общая сумма выплат после полного погашения кредита составила 836 тысяч рублей.
В июле 2016 года планируется взять кредит в банке в размере S тыс. рублей, где S — натуральное число, на 3 года. Условия его возврата таковы
− каждый январь долг увеличивается на 17,5% по сравнению с концом предыдущего года;
− с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
− в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
| Месяц и год | Июль 2016 | Июль 2017 | Июль 2018 | Июль 2019 |
| Долг (в тыс. рублей) |
S | 0,9S | 0,4S | 0 |
Найдите наименьшее значение S, при котором каждая из выплат будет составлять целое число тысяч рублей.
Источник: ЕГЭ по математике 06.06.2016. Основная волна. Вариант 703 (C часть).
По бизнес-плану предполагается вложить в четырёхлетний проект целое число миллионов рублей. По итогам каждого года планируется прирост средств вкладчика на 20% по сравнению с началом года. Начисленные проценты остаются вложенными в проект. Кроме этого, сразу после начислений процентов нужны дополнительные вложения: по 20 миллионов рублей в первый и второй годы, а также по 10 миллионов в третий и четвёртый годы. Найдите наименьший размер первоначальных вложений, при котором общая сумма средств вкладчика за два года станет больше 100 миллионов, а за четыре года станет больше 170 миллионов рублей.
Всего: 71 1–20 | 21–40 | 41–60 | 61–71
07
Май 2015
Категория: 15 (С4) Практич. задачиТ/P A. Ларина
2015-05-07
2015-09-04
В новом формате ЕГЭ по математике задание значится как «Задание №17»
Смотрите также №15, №16, №17, №18, №20.
Алексей вышел из дома на прогулку со скоростью км/ч. После того, как он прошел 6 км, из дома следом за ним выбежала собака Жучка, скорость которой была на 9 км/ч больше скорости Алексея. Когда Жучка догнала хозяина, они повернули назад и вместе возвратились домой со скоростью 4 км/ч. Найдите значение
, при котором время прогулки Алексея окажется наименьшим. Сколько при этом составит время его прогулки?
Решение:
Алексей (выйдя из дома со скоростью км/ч) на путь в 6 км потратил
часов.
Пусть после этого Алексей до встречи с Жучкой прошел еще км, на что ушло
часов.
За тоже время ( ч) Жучка пробежала
км со скоростью
км/ч.
Тогда откуда
Время прогулки Алексея, с учетом того, что вместе с Жучкой они возвращались домой со скоростью км/ч, составило, таким образом,
часов (или
часов).
Рассмотрим функцию и найдем
, при котором функция принимает наименьшее значение (а также само наименьшее значение).
– точка минимума, в ней и достигается наименьшее значение функции.
(ч).
Ответ: 6 км/ч; 4 часа 10 минут.
Автор: egeMax |
комментариев 7
0,1(7000+2000n-2000)2000
500+200n2000
200n
n
n=8
Ответ: 8года.
3.3 Задачи на оптимизацию.
Задача №1.
У фермера есть два поля, каждое площадью 100 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 400 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором — 400 ц/га.Фермер может продавать картофель по цене 10 000 руб. за центнер, а свёклу — по цене 11 000 руб. за центнер. Какой наибольший доход может получить фермер?
Решение:
Вся площадь: 100 га
Составим функцию полного дохода:
∑(x,k) = 4000000x+3300000kx→наиб
Заметим, что x+kx=100, т.е. x=где k
∑(k) = +→наиб
∑(k) = →наиб
Возьмём производную этой функции
= =
Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить картофелем, при этом доход будет 4000000рублей
Из второй таблицы видно, что свекла имеет, как большую урожайность, так и большую цену за центнер, следовательно, второе поле нужно засадить свеклой.При этом доход будет 40011000рублей
Полный доход составляет 400 млн + 440 млн = 840 млн рублей.
Ответ: 840 млн рублей.
Задача №2.
У фермера есть два поля, каждое площадью 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 500 ц/га, а на втором — 300 ц/га. Урожайность свёклы на первом поле составляет 300 ц/га, а на втором – 500 ц/га. Фермер может продать картофель по цене 5000 руб. за центнер, а свёклу — по цене 8000 руб. за центнер. Какой наибольший доход может получить фермер?
Вся площадь: 10 га
Составим функцию полного дохода:
∑(x,k) = 2500000x+2400000kx→наиб
Заметим, что x+kx=10, т.е. x=где k
∑(k) = +→наиб
∑(k) = →наиб
Возьмём производную этой функции
= =
Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при k=0. Это означает, что всё первое поле нужно засадить картофелем, при этом доход будет 2500000рублей
Из второй таблицы видно, что свекла имеет, как большую урожайность, так и большую цену за центнер, следовательно, второе поле нужно засадить свеклой. При этом доход будет 5008000рублей
Полный доход составляет 25 млн + 40 млн = 65 млн рублей.
Ответ: 65млн рублей.
Задача №3.
Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера «люкс» площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» — 4000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?
Решение:
Общая площадь: 981
Составим функцию полного дохода:
∑(x,y) = 2000x+4000y→наиб
Заметим, что 27x+45y981, т.е. x где y , т.е.y
∑(y) = +4000y→наиб
∑(y) = →наиб
Возьмём производную этой функции
=
Значит функция возрастает во всей области определения, т.е. принимает своё наибольшее значение при y=21. Это означает, что номеров люкс будет 21. Проверим общую площадь: 45ер. При этом полный доход будет рублей.
Ответ: 86000 рублей.
Задача №4.
Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 30 квадратных метров и номера «люкс» площадью 40 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 940 квадратных метров. Предприниматель может определить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 4000 рублей в стуки, а номер «люкс» — 5000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
Решение:Общая площадь : 940
Составим функцию полного дохода:
∑(x,y) = 4000x+5000y→наиб
Заметим, что 30x+40y940, т.е. x где y , т.е.y
∑(y) = +5000y→наиб
∑(y) = →наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=0. Это означает, что стандартных номеров будет 940. Проверим общую площадь: 30ер на номер люкс. При этом полный доход будет рублей.
Ответ: 125000 рублей.
Задача №5.
Антон является владельцем двух заводов в разных городах. На заводах производится абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t2 часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе,Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, — 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение: Оплата труда в неделю : 900000рублей
Составим функцию количества единиц товара:
∑(x,y) = x+y→наиб
Заметим, что 250+200900000, т.е. x где y
∑(y) = +y→наиб
Возьмём производную этой функции
= +1 =
Найдём нули производной: =0
=0
0,64=(3600-)
1,44=3600
y=50
Функция принимает своё наибольшее значение при y=50 (точка максимума).
x==40
Найдём количество единиц товара :+50 = 90
Ответ: 90 единиц товара.
Задача №6.
Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно t2 часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение:Оплата труда в неделю: 5000000рублей
Составим функцию количества единиц товара:
∑(x,y) = 3x+4y→наиб
Заметим, что 500+5005000000, т.е. x где y
∑(y) =3 +4y→наиб
Возьмём производную этой функции
= 3+4 =
Найдём нули производной: =0
=0
9=16(10000-)
25=1600000
y=80
Функция принимает своё наибольшее значение при y=80 (точка максимума).
x==60
Найдём количество единиц товара: 3+480 = 180+320 = 500
Ответ: 500 единиц товара.
Задача №7.
Борис является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно t 2 часов в неделю, то за эту неделю они производят t единиц товара.За каждый час работы на заводе, расположенном в первом городе, Борис платит рабочему 500 рублей, а на заводе, расположенном во втором городе, — 200 рублей.Борису нужно каждую неделю производить 70 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
Решение: 70 единиц товара
Составим функцию еженедельной оплаты труда:
∑(x,y) = 500→наим
Заметим, что x+y70, т.е. x где y
∑(y) =500→наим
∑(y) =500 =700-70000y+2450000
Возьмём производную этой функции
= 1400y-70000
Найдём нули производной: 1400y-70000=0
y=50
Функция принимает своё наименьшее значение при y=50 (точка минимума).
x
Найдёмеженедельную оплату труда:+200 = 500+200500000=700000
Ответ: 700тысяч рублей.
Задача №8.
Фёдор является владельцем двух заводов в разных городах.Назаводахпроизводятсяабсолютноодинаковыеприборы,ноназаводе,расположенном в первом городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятсясуммарно 3t2часоввнеделю,тозаэтунеделюонипроизводят t приборов;если рабочие на заводе,расположенномво втором городе, трудятся суммарно 4t2 часов внеделю,онипроизводят tприборов.За каждый час работы (на каждом из заводов) Фёдор платит рабочему 1тысячуруб.Необходимо,чтобызанеделюсуммарнопроизводилось30приборов.Какуюнаименьшуюсуммупридетсятратитьвладельцузаводов еженедельно на оплату трударабочих?
Решение: 30 единиц товара
4y2
y
1000
4000
Составим функцию еженедельной оплаты труда:
∑(x,y) = 3000→наим
Заметим, что x+y30, т.е. x где y
∑(y) =3000→наим
∑(y) =3000 =7000-180000y+2700000
Возьмём производную этой функции
= 14000y-180000
Найдём нули производной: 14000y-180000=0
y==12
Функция принимает своё наименьшее значение при y=12 (точка минимума).
Пусть y=12, тогда x=18
Найдёмеженедельную оплату труда:+400 = 3000+4000000=1548000
Пусть y=13, тогда x=17
Найдёмеженедельную оплату труда:+400 = 30004000000=1543000
Ответ: 1543000 рублей.
Задача №9.
В двух областях есть по 160 рабочих, каждый из которых готов трудиться по 5 часов в сутки на добыче алюминия или никеля. В первой области один рабочий за час добывает 0,1 кг алюминия или 0,1 кг никеля. Во второй области для добычи x кг алюминия в день требуется x2 человеко-часов труда, а для добычи у кг никеля в день требуется у2 человеко-часов труда.
Для нужд промышленности можно использовать или алюминий, или никель, причём 1 кг алюминия можно заменить 1 кг никеля. Какую наибольшую массу металлов можно за сутки суммарно добыть в двух областях?
Решение:
Из таблицы видно, что в первой области совершенно одинаковые условия добывания алюминия и никеля. Это означает, что в первой области алюминия и никеля будут добывать поровну по = 40 кг. Всего 80 кг.
Во второй области: x2 +y2=160
x2 +y2=800
x=20, y=20. Всего 40 кг.
Ответ: 120кг.
Задача №10.
В двух шахтах добывают алюминий и никель. В первой шахте имеется 60 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 2 кг алюминия или 3 кг никеля. Во второй шахте имеется 260 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 2 кг никеля.
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог произвести наибольшее количество сплава. Сколько килограммов сплава при таких условиях ежедневно сможет произвести завод?
Решение: 60 человек по 5 часов в день
260 человек по 5 часов в день Получаем, что всего алюминия производят 10x+15y
никеля:15(60-x)+ 10(260-y)=3500-15x-10y
Так как для сплаванеобходимо , чтобы на2 кг алюминия приходился 1 кг никеля, то: 10x+15y=2(3500-15x-10y)
10x+15y=7000-30x-20y
40x=7000-35y
x = =
Составим функцию массы сплава:
∑(x,y) = 10x+15y+3500-15x-10y→наиб
∑(x,y) = 3500-5x+5y →наиб
∑(y) = 3500-5 +5y →наиб
∑(y) = 3500-5 +5y →наиб
∑(y) = →наиб
Возьмём производную этой функции
=
Значит функция возрастает во всей области определения, т.е. принимает своё наибольшее значение при наибольшем значенииy.
Так как x = то 1400-7y0 , y.
Проверим значение у=200, тогда x=0.
Масса сплава: 3500-5+5=4500
Ответ: 4500 кг.
Задача №11.
Фабрика, производящая пищевые полуфабрикаты, выпускает блинчики со следующими видами начинки: ягодная и творожная. В данной ниже таблице приведены себестоимость и отпускная цена, а также производственные возможности фабрики по каждому виду продукта при полной загрузке всех мощностей только данным видом продукта.
Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции каждого вида должно быть выпущено не менее 15 тонн. Предполагая, что вся продукция фабрики находит спрос (реализуется без остатка), найдите максимально возможную прибыль, которую может получить фабрика от производства блинчиков за 1 месяц
Решение
Пусть xтонн выпускает фабрика блинчиков с ягодами, а y тонн – с творогом. Тогда по условию имеем :x
Составим функцию прибыли:
∑(x,y) = 30x+35y→наиб
Пусть производственная возможность равна 1, тогда + = 1
75x + 90y = 6750
x = 90 – 1,2y
∑(y) = 30(90 – 1,2y)+35y→наиб
∑(y) = 2700 — y→наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=15. Тогда x = 90-1,2
При этом максимальная прибыль будет рублей.
Ответ: 2685000 рублей.
Задача №12.
Консервный завод выпускает фруктовые компоты в двух видах тары — стеклянной и жестяной. Производственные мощности завода позволяют выпускать в день 90 центнеров компотов в стеклянной таре или 80 центнеров в жестяной таре. Для выполнения условий ассортиментности, которые предъявляются торговыми сетями, продукции в каждом из видов тары должно быть выпущено не менее 20 центнеров. В таблице приведены себестоимость и отпускная цена завода за 1 центнер продукции для обоих видов тары.
Предполагая, что вся продукция завода находит спрос (реализуется без остатка), найдите максимально возможную прибыль завода за один день (прибылью называется разница между отпускной стоимостью всей продукциии её себестоимостью).
Решение
Пусть xцентнеров выпускает фабрика в стеклянной таре, а y центнеров – в жестяной. Тогда по условию имеем :x
Составим функцию прибыли:
∑(x,y) = 600x+650y→наиб
Пусть производственная возможность равна 1, тогда + = 1
80x + 90y = 7200
x = 90 – 1,125y
∑(y) = 600(90 – 1,125y)+650y→наиб
∑(y) = 54000 — 25y→наиб
Возьмём производную этой функции
=
Значит функция убывает во всей области определения, т.е. принимает своё наибольшее значение при y=20. Тогда x = 90-1,12
При этом максимальная прибыль будет рублей.
Ответ: 53500 рублей.
3.4 Нестандартные задачи
Задача №1.
Два велосипедиста равномерно движутся по взаимно перпендикулярным дорогам по направлению к перекрестку этих дорог. Один из них движется со скоростью 40 км/ч и находится на расстоянии 5 км от перекрестка, второй движется со скоростью 30 км/ч и находится на расстоянии 3 км от перекрестка. Через сколько минут расстояние между велосипедистами станет наименьшим? Каково будет это наименьшее расстояние?
Решение:
Составим функцию квадрата расстояния между велосипедистами:
∑(t) = →наим, где t
∑(t) = 25-400t+1600→наим
∑(t) = 2500→наим
Возьмём производную этой функции
= 5000t-580
Найдём нули производной: 5000t-580=0
t===
Функция принимает своё наименьшее значение при t=ч = 60(точка минимума).
Найдём расстояние между велосипедистами: = = ===0,6
Ответ: 0,6км, 6,96 минут.
Задача №2.
Бриллиант массой 20 карат был разбит на две части после чего его стоимость уменьшилась на 25,5%.а) Найдите массы частей на которые был разбит бриллиант если известно, что цена бриллианта пропорциональнаквадрату его массы.б) На какое максимальное число процентов может уменьшиться цена бриллианта разбитого на две части.
Решение:
M=20 карат, S— стоимость бриллианта
S=km,S1=km1,S2=km2
Пустьm=x,тогдаm=20-x
-
S1+S2=0,745S
kx2+k(20-x)2=0,745k202
x2+(20-x)2=298
x2+400-40x+102=0
x2-20x+51=0
x1=17, x2=3
Ответ: массы частей 17 и 3 карат.
-
Цена бриллианта максимально снизится, если обе части будут по 10 карат
S1+S2=aS
k102+k102=a202k
100+100=a400
a=200/400=0,5
Ответ: на 50%
Задача №3
В одной стране в обращении находились 1000000 долларов, 20% из которых были фальшивыми. Некая нехорошая структура стала ввозить в страну по 100000 долларов в месяц, 10% из которых были фальшивыми. В это время другая структура стала вывозить из страны 50000 долларов ежемесячно, из которых 30% оказались фальшивыми. Через сколько месяцев содержания фальшивых долларов в стране составит 5%?
Решение:
n-количество месяцев
-
200000-5000n =0,05(1000000+50000n )
200000-5000n =50000+2500n
-7500n = -150000
n=20
Ответ: 20 месяцев
Задача №4
Два брокера купили акции одного достоинства на сумму 3640 рублей.Когда цена на эти акции возросла, они продали часть акций на сумму 3927 рублей. Первый брокер продал 75% своих акций, а второй – 80%. При этом сумма от продажи акций, полученная вторым брокером, на 140% больше суммы первого. На сколько процентов возросла цена одной акции?
Решение:
k— первоначальная цена 1 акции
x – штук купил первый брокер
y – штук купил второй
z – конечная цена 1 акции
Составим систему уравнений:
3)
y = = 2,25x
-
k(x+y)=3640
k(x+2.25x)=3640
k = = =
-
z(0,75x+0,8y)=3927
z(0,75х+1,8x)=3927
z2,55x=3927
z= = =
4)Найдём, на сколько процентов возросла цена одной акции
k= — 100%
z = — a%
a= 137,5%
Ответ: на 37,5%
Задача №5.
Строительство нового завода стоит 115млн рублей. Затраты на производство x тыс. единиц продукции на таком заводе равны0,5 x2+x+9млн рублей в год. Если продукцию завода продать по цене p тыс. рублей за единицу, то прибыль фирмы (в млн рублей) за один год составит
px-(0,5 x2+x+9). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении pстроительство завода окупится не более чем за 5 лет?
Решение
Составим функцию прибыли:
∑(x,p) =px-(0,5 x2+x+9)→наиб
∑(x,p) =px-0,5 x2—x-9
Возьмём производную этой функции
= p—x-1
Найдём нули производной: p—x-1=0
x = p-1
Функция принимает своё наибольшее значение приx = p-1(точка минимума).
Найдём прибыль:
∑(p) =p(p-1)-0,5 (p-1)2-(p-1)-9 = 0,5p2—p-8,5
По условию строительство завода должно окупиться не более, чем за 5 лет. То есть за 5 лет прибыль должна быть не меньше 115млн рублей.
5(0,5p2—p-8,5115
0,5p2—p-8,5-23=0
p2-2p-63=0
p1=9, p2=-7
Ответ: 9 тысяч рублей.
4.Заключение
В данной работе рассмотрены основные методы решения задач на кредит, вклады и оптимизацию. Тема работы очень актуальна, так как все рассматриваемые задачи взяты из материалов по подготовке к ЕГЭ по математике «Профиль». Надеюсь, что данная работа будет полезна учащимся 10-11 класса, а также преподавателям математики.
5.Список использованной литературы:
1. ЕГЭ 2018под редакцией А. Л. Семенова, И.В. Ященко
2. Открытый банк заданий ЕГЭfipi.ru
3. Сайт «Решу ЕГЭ»
4. Сайт «Алекс Ларин»
-
| 3655 | Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD=3RD. Прямые AR и PD пересекаются в точке Q , AD=2BC. a) Докажите, что точка Q – середина отрезка AR б) Найдите площадь треугольника APQ |
Площадь трапеции ABCD равна 30. Точка Р – середина боковой стороны АВ. Точка R на боковой стороне CD выбрана так, что 2CD=3RD ! Тренировочный вариант 221 от Ларина Задание 16 # Решение пункта Б | |
| 3471 | а) Решите уравнение cos(3x)/(2sin(x)+sqrt(2))=sin(x)/(2sin(x)+sqrt(2)) б) Найдите все корни уравнения, принадлежащие отрезку [0; pi]. |
а) Решите уравнение cos3x /(2sinx + sqrt2 = sinx /2sinx +sqrt2 ! Тренировочный вариант 399 от Ларина Задание 12 | |
| 3470 | В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73. Высота пирамиды проходит через точку пересечения диагоналей основания и равна 4. а) Докажите, что две боковые грани являются прямоугольными треугольниками. б) Найдите площади двух других боковых граней |
В основании пирамиды лежит параллелограмм со сторонами 8 и 10, а его большая диагональ равна 2sqrt73 ! Тренировочный вариант 399 от Ларина Задание 13 | |
| 3469 | Решите неравенство 64^x/(36^x-27^x)+(4(16^x-12^x))/(16^x-2*12^x+9^x). <= 16^(x+0.5)/(12^x-9^x). |
Решите неравенство 64^x / 36^x -27^x +4(16^x-12^x) /16^x -2*12^x+9^x <= 16^ x+0,5 / 12^x-9^x ! Тренировочный вариант 399 от Ларина Задание 14 |
|
| 3468 | На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2. а) Докажите, что площадь четырехугольника МКСN составляет 11/24 площади квадрата ABCD. б) Найдите синус угла между диагоналями четырехугольника МКCN |
На сторонах АВ, ВС и АD квадрата ABCD взяты соответственно точки М, К и N, такие, что АМ : МВ = 3 : 1, ВК : КС = 2 : 1 и АN : ND = 1 : 2 ! Тренировочный вариант 399 от Ларина Задание 16 | |
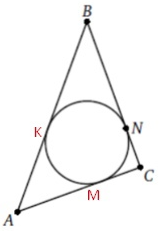
| 3467 | В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС. В эту трапецию вписали окружность с центром О. Прямая АО пересекает продолжение отрезка ВС в точке Е а) Докажите, что AD=CE+CD б) Найдите площадь трапеции ABCD, если АЕ=10, /_BAD=60^@ |
В трапеции АВСD боковая сторона CD перпендикулярна основаниям AD и ВС ! Тренировочный вариант 398 от Ларина Задание 16 | |
| 3466 | Найдите значение выражения ((root(4)(3)-root(4)(27))^2+7)((root(4)(3)+root(4)(27))^2-7) |
Найдите значение выражения ((root(4)(3) -root(4)(27))2 +7 ((root(4)(3)+root(4)(27))2 -7) ! Тренировочный вариант 398 от Ларина Задание 6 | |
| 3465 | Имеются два сплава, состоящие из цинка, меди и олова. Известно, что первый сплав содержит 40% олова, а второй ‐ 25% меди. Процентное содержание цинка в первом и втором сплавах одинаково. Соединив 150 кг первого сплава и 250 кг второго, получили новый сплав, в котором оказалось 30% цинка. Сколько килограммов олова содержится в получившемся сплаве? |
Имеются два сплава, состоящие из цинка, меди и олова ! Тренировочный вариант 398 от Ларина Задание 9 | |
| 3464 | а) Решите уравнение sqrt(2sin(x)+sqrt(2))*log_{4}(2cos(x))=0 б) Найдите все корни уравнения, принадлежащие отрезку [-(5pi)/2; -pi]. |
а) Решите уравнение sqrt(2sinx +sqrt2) log4 2cosx = 0 ! Тренировочный вариант 398 от Ларина Задание 12 | |
| 3463 | SMNK – правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР:PS=1:3, точка L – середина ребра MN. а) Доказать, что плоскости SLK и MPN перпендикулярны б) Найдите длину отрезка PL, если длина ребра MN равна 4 |
SMNK – правильный тетраэдр ! Тренировочный вариант 398 от Ларина Задание 13 | |

Показана страница 1 из 89
Задание 1
Решите уравнение $$frac{3^{x^2}-81}{x-2}=0.$$ Если уравнение имеет более одного корня, в ответе укажите больший из них.
Ответ: -2
Скрыть
ОДЗ: $$xneq2$$
$$3x^2=81=3^4$$
$$x^2=4$$
$$x=−2$$
$$x=2$$ – не подходит под ОДЗ
Задание 2
Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,03. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,96. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,03. Найдите вероятность того, что случайно выбранная изготовленная батарейка будет забракована системой контроля.
Ответ: 0,0579
Скрыть
$$P(A)=P(A_1+A_2)=P(A_1)+P(A_2)$$ – вероятность наступления 2-х несовместных событий
$$A_1$$ – исправная батарейка забракована системой
$$A_2$$ – неисправная батарейка забракована системой
$$P(A_1)=0,97cdot0,03$$
$$P(A_2)=0,03cdot0,96$$
$$P(A)=0,97cdot0,03+0,03cdot0,96=0,0579$$
Задание 3
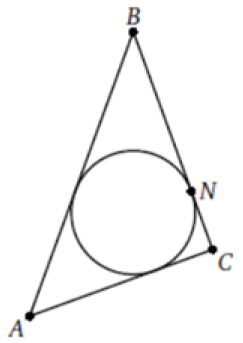
Окружность, вписанная в треугольник ABC, касается его стороны BC в точке N. Известно, что BN = 15 и AC = 17. Найдите периметр треугольника.
Ответ: 64
Скрыть
$$P=AB+AC+BC$$
$$P=AK+BK+BN+NC+AC$$
По свойству касательных, проведенных из одной точки
$$AK=AM$$
$$NC=MC$$
$$BK=BN=15$$
$$AC=AM+MC=AK+NC$$
Значит
$$P=17+17+15+15=64$$
Задание 4
Найдите значение выражения $$frac{9^{x+11}cdot2^{3x+8}}{3^{2x+21}cdot4^{x+4}}$$ при $$x = 2$$
Ответ: 12
Скрыть
$$frac{3^{2x+22}cdot2^{3x+8}}{3^{2x+21}cdot2^{2x+8}}=3cdot2^x=12$$
Задание 5
Основанием наклонной призмы $$ABCDA_1B_1C_1D_1$$ является квадрат $$ABCD,$$ а диагональ $$AC_1$$ призмы перпендикулярна плоскости основания. Найдите площадь основания призмы, если $$AC_1=2sqrt{7}, AA_1=6.$$
Ответ: 4
Скрыть
Пусть $$a$$ — сторона квадрата
Если диагональ перпендикулярна плоскости основания, то из прямоугольного треугольника мы можем найти диагональ квадрата, который лежит в основании.
$$sqrt{36-14cdot7}=2sqrt{2}=asqrt{2}$$
$$a=2$$
$$S=4$$
Задание 6
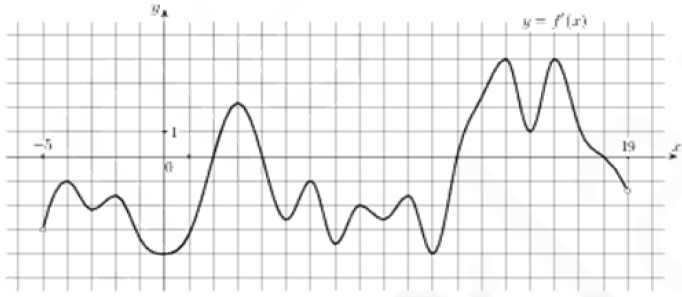
На рисунке изображен график $$y=f'(x)$$ — производной функции $$f(x),$$ определенной на интервале $$(-5; 19).$$ Найдите количество точек максимума функции $$f(x),$$ принадлежащих отрезку $$[-3; 15].$$
Ответ: 1
Скрыть
Точка максимума будет там, где знак производной меняется с “+” на “-”
Задание 7
Скорость колеблющегося на пружине груза меняется по закону $$v(t)=3sinfrac{pi t}{4}$$ (см/с), где $$t$$ — время в секундах. Какую долю времени из первой секунды скорость движения превышала 1,5 см/с? Ответ выразите десятичной дробью, если нужно, округлите до сотых.
Ответ: 0,33
Скрыть
$$3cdotsinfrac{pi t}{4}>1,5$$
$$sinfrac{pi t}{4}>frac{1}{2}$$
$$frac{pi}{6}+2pi n<frac{pi t}{4}<frac{5pi}{6}+2pi n$$
$$frac{2}{3}+8n<t<frac{10}{3}+8n$$
$$n=0$$
$$frac{2}{3}<t<3frac{1}{3}$$
$$frac{2}{3}<t<1$$
Получаем, что $$1−frac{2}{3}=frac{1}{3}approx0,33$$ доля от первой секунды скорость была больше 1,5
Задание 8
Аркадий продал партию компьютеров, а Борис продал партию принтеров, и их выручка оказалась одинаковой. «Если бы принтер стоил столько же, сколько компьютер, я бы получил 192 млн. рублей» — сказал Борис. «Если бы компьютер стоил столько же, сколько принтер, я бы получил 75 млн. рублей» — ответил Аркадий. На сколько процентов компьютер дороже принтера?
Ответ: 60
Скрыть
Пусть $$x, y$$ – цена принтера и компьютера соответственно, $$k,n$$ – кол-во проданных принтеров и компьютеров соответственно.
$$xcdot k=ycdot n$$
$$left{begin{matrix}
xcdot n=192\
ycdot k=75
end{matrix}right.$$
Решая систему, получаем $$frac{x}{y}=1,6$$
$$Rightarrow 60%$$
Задание 9
На рисунке изображен график функции $$f'(x)=acdottg x+b.$$ Найдите $$b.$$
Ответ: -3
Скрыть
$$1=acdottgfrac{pi}{4}+b$$
$$−3=acdottg0+b$$
$$b=−3$$
Задание 10
В одном ресторане в г. Тамбове администратор предлагает гостям сыграть в «Шеш-беш»: гость бросает одновременно 2 игральные кости. Если он выбросит комбинацию 5 и 6 очков хотя бы один раз из двух попыток, то получит комплимент от ресторана: чашку кофе или десерт бесплатно. Какова вероятность получить комплимент? Результат округлите до сотых.
Ответ: 0,11
Скрыть
Всего благоприятных вариантов из 36 два: 5,6 и 6,5
Найдем вероятность того, что гостю ни разу не выпала комбинация 5,6:
$$P(A)=(1-frac{2}{36})cdot(1-frac{2}{36})$$
$$P_{иск}=1−P(A)=frac{35}{324}approx0,11$$
Задание 11
Найдите наибольшее значение функции $$y=12sin x-6sqrt{3}x+sqrt{3}pi+6$$ на отрезке $$[0;frac{pi}{2}].$$
Ответ: 12
Скрыть
Найдем критические точки:
$$y’=0$$
$$12cos x−6sqrt{3}=0$$
$$cos x=frac{sqrt{3}}{2}$$
$$x=pmfrac{pi}{6}+2pi n$$
Под отрезок попадает только $$x=frac{pi}{6}$$
Проверкой методом интервалов эта точка и является точкой максимума
$$y(frac{pi}{6})=12$$
Задание 12
А) Решите уравнение $$frac{4^{x+frac{1}{2}}=2^{x+1}-2^{x+frac{1}{2}}+sqrt{2}}{sin x+sin2x}=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-frac{pi}{2};frac{pi}{2}]$$
Ответ: А)$$-0,5$$ Б)$$-0,5$$
Задание 13
В кубе ABCDA1B1C1D1 точки K, L и М — середины ребер АВ, В1С1 и DD1
А) Докажите, что сечение куба плоскостью KLM является правильным многоугольником.
Б) Найдите расстояние от точки А до плоскости KLM, если ребро куба равно 2.
Ответ: $$frac{1}{sqrt{3}}$$
Задание 14
Решите неравенство: $$(6+sqrt{35})^{2x}-frac{7-sqrt{35}}{(6-sqrt{35})^x}+6>sqrt{35}$$
Ответ: $$(-infty;-1),(0;infty)$$
Задание 15
В начале 1977 года Алишер положил в пустой сейф 1 млн. руб. В начале каждого последующего года он вынимает из сейфа m% имеющихся там рублей. При каком значении m он вынет из сейфа в начале 1982 года максимальную сумму?
Ответ: 20
Задание 16
В выпуклом четырехугольнике ABCD диагональ АС является биссектрисой угла BAD и пересекается с диагональю BD в точке Е. Известно, что около четырехугольника ABCD можно описать окружность.
А) Докажите, что $$AEcdot AC = ADcdot AB$$
Б) Найдите АЕ, если известно, что ВС=7, СЕ=4.
Ответ: 8,25
Задание 17
Найдите все значения параметра $$a,$$ при каждом из которых уравнение
$$|log_5(x^2)-a|-|log_5 x+2a|=(log_5 x)^2$$
имеет ровно четыре решения.
Ответ: $$(-frac{1}{12};0),(0;frac{1}{12})$$
Задание 18
А) Можно ли в выражении $$ln 5 * ln 6 * ln 7 * ln8 * ln10 * ln12 * ln14$$ вместо всех знаков * так расставить знаки “+” и “-“, чтобы в результате получился ноль?
Б) Можно ли в выражении $$ln 6 * ln 7 * ln 8 * ln12 * ln14 * ln 24 * ln 32$$ вместо всех знаков * так расставить знаки “+” и “-“, чтобы в результате получился ноль?
В) Какое наибольшее количество попарно различных чисел можно выбрать из набора $$ln 7, ln 8,…ln 20$$ и расставить знаки “+” и “-“ так, чтобы их сумма стала равна нулю?
Ответ: А) да, Б) нет, В) 9
2 декабря 2021
В закладки
Обсудить
Жалоба
В данной работе рассмотрены основные методы решения задач на кредит, вклады и оптимизацию.
Разобраны 8 типов заданий
→ 1 тип: Нахождение количества лет (месяцев) выплаты кредита. (Аннуитетные платежи) — 3 задачи.
→ 2 тип: Вычисление процентной ставки по кредиту. (Фиксированные платежи) – 3 задачи.
→ 3 тип: Нахождение суммы кредита. (Аннуитетные платежи)- 3 задачи.
→ 4 тип: Нахождение ежегодного (ежемесячного) транша. (Аннуитетные платежи)- 3 задачи.
→ 5 тип: Нахождение разницы. (Аннуитетные платежи) – 3 задачи.
→ 6 тип: Задачи, связанные с известным остатком. (Фиксированные платежи)- 3 задачи.
→ 7 тип: Задачи, связанные с дифференцированными платежами.- 3 задачи.
→ 8 тип: Нестандартные задачи, связанные с кредитом.- 4 задачи.
50ek.docx